题目描述
This past fall, Farmer John took the cows to visit a corn maze. But this wasn't just any corn maze: it featured several gravity-powered teleporter slides, which cause cows to teleport instantly from one point in the maze to another. The slides work in both directions: a cow can slide from the slide's start to the end instantly, or from the end to the start. If a cow steps on a space that hosts either end of a slide, she must use the slide.
The outside of the corn maze is entirely corn except for a single exit.
The maze can be represented by an N x M (2 <= N <= 300; 2 <= M <= 300) grid. Each grid element contains one of these items:
* Corn (corn grid elements are impassable)
* Grass (easy to pass through!)
* A slide endpoint (which will transport a cow to the other endpoint)
* The exit
A cow can only move from one space to the next if they are adjacent and neither contains corn. Each grassy space has four potential neighbors to which a cow can travel. It takes 1 unit of time to move from a grassy space to an adjacent space; it takes 0 units of time to move from one slide endpoint to the other.
Corn-filled spaces are denoted with an octothorpe (#). Grassy spaces are denoted with a period (.). Pairs of slide endpoints are denoted with the same uppercase letter (A-Z), and no two different slides have endpoints denoted with the same letter. The exit is denoted with the equals sign (=).
Bessie got lost. She knows where she is on the grid, and marked her current grassy space with the 'at' symbol (@). What is the minimum time she needs to move to the exit space?
输入格式
第一行:两个用空格隔开的整数 NN 和 MM。
第 2\sim N+12∼N+1 行:第 i+1i+1 行描述了迷宫中的第 ii 行的情况(共有MM个字符,每个字符中间没有空格)。
输出格式
一个整数,表示起点到出口所需的最短时间。
题意翻译
奶牛们去一个 N\times MN×M 玉米迷宫,2 \leq N \leq 300,2 \leq M \leq3002≤N≤300,2≤M≤300。
迷宫里有一些传送装置,可以将奶牛从一点到另一点进行瞬间转移。这些装置可以双向使用。
如果一头奶牛处在这个装置的起点或者终点,这头奶牛就必须使用这个装置。
玉米迷宫除了唯一的一个出口都被玉米包围。
迷宫中的每个元素都由以下项目中的一项组成:
- 玉米,
#表示,这些格子是不可以通过的。- 草地,
.表示,可以简单的通过。- 传送装置,每一对大写字母 \tt{A}A 到 \tt{Z}Z 表示。
- 出口,
=表示。- 起点,
@表示奶牛能在一格草地上可能存在的四个相邻的格子移动,花费 11 个单位时间。从装置的一个结点到另一个结点不花时间。
输入输出样例
输入 #1复制
5 6 ###=## #.W.## #.#### #.@W## ######输出 #1复制
3说明/提示
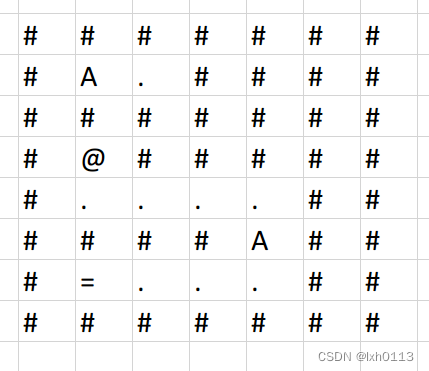
例如以下矩阵,N=5,M=6N=5,M=6。
###=## #.W.## #.#### #.@W## ######唯一的一个装置的结点用大写字母 \tt{W}W 表示。
最优方案为:先向右走到装置的结点,花费一个单位时间,再到装置的另一个结点上,花费 00 个单位时间,然后再向右走一个,再向上走一个,到达出口处,总共花费了 33 个单位时间。
1.这个题目我从全部WA然后大部分RE最后全部AC,真的是不容易啊(本来都不抱希望的了)。这是一个典型的BFS问题,是可以直接使用BFS模板去套用。
2.这个题目比较多的细节。首先就是传送门,译文说只有一对W,但是我后面下载了我测试错误的例子。是发现不止的,还有其他的。而且可能只有一个装置(这个不是很确定也是看题解有大佬说的)。关于传送门刚开始我想着把所有的列出来,但是一直没有AC几个,就试着和写题解的大佬一样直接去查找另外一个就ok,果真又AC了几个。但是有一个特别特别要注意的点,我是改了这个点之后,我才从52到100分的!就是我们在判别的时候,我们会搜到俩个,一个是我们本身进去的那一个,另外一个是要到的那一个。我们写if的时候不能写 i!=__&&j!=__。我们要写||,写&&的会出现万一装置在同一行或者同一列会出错。而||不会,因为只要有一个坐标不一样就说明是另外一个装置。
3.另外就是BFS开队列建议一定要把tail++这种类似自增语句改成tail=(tail+1)%MAXSIZE这样,我之前没改全是RE,因为我们不知道它的数组究竟要开多大,我们这么写是可以“废物利用”的。而主循环我们要写while(head!=tail),不要写成while(head<tail),因为tail可能已经走完一圈到前面了,会提前结束循环的。
4.在写的时候也一定要用数组标记走过,否则不会过。而且还会出现TLE的情况(不要问我怎么知道的)。
5.另外就是到传送门另一端的时候步数要+1,传送门不要标记!!!因为会出现以下情况,一定要去另一端转一转。再次回来再去出口。
代码如下:
#include<stdio.h>
#define N 400
#include<ctype.h>
char str[N][N],book[N][N];
int n,m,start[2],end[2];
int head,tail;
struct node
{
int x;
int y;
int s;
}cow[N*N+10];
int seek(struct node *a,char ch)
{
int i,j;
for(i=0;i<n;i++)
{
for(j=0;j<m;j++)
{
if(str[i][j]==ch&&(i!=(a->x)||j!=(a->y)))
{
a->x=i;a->y=j;return 0;
}
}
}
}
int bfs()
{
int i,j,tx,ty;
int k[4][2]={{0,-1},{-1,0},{0,1},{1,0}};
head=tail=0;
book[start[0]][start[1]]=1;
cow[tail].x=start[0];
cow[tail].y=start[1];
cow[tail].s=0;
tail=(tail+1)%(N*N+10);
while(head!=tail)
{
for(i=0;i<4;i++)
{
tx=cow[head].x+k[i][0];
ty=cow[head].y+k[i][1];
if(tx>=0&&tx<n&&ty>=0&&ty<m&&str[tx][ty]!='#')
{
if(str[tx][ty]=='.'&&book[tx][ty]==0)
{
book[tx][ty]=1;
cow[tail].x=tx;
cow[tail].y=ty;
cow[tail].s=cow[head].s+1;
tail=(tail+1)%(N*N+10);
}
else if(str[tx][ty]>='A'&&str[tx][ty]<='Z')
{
cow[tail].x=tx;
cow[tail].y=ty;
cow[tail].s=cow[head].s+1;
seek(&(cow[tail]),str[tx][ty]);
tail=(tail+1)%(N*N+10);
}
else if(tx==end[0]&&ty==end[1])
{
return cow[head].s+1;
}
}
}
head=(head+1)%(N*N+10);
}
}
int main()
{
int i,j;
scanf("%d%d",&n,&m);
for(i=0;i<n;i++)
scanf("%s",str[i]);
for(i=0;i<n;i++)
{
for(j=0;j<m;j++)
{
if(str[i][j]=='@')
{
start[0]=i;start[1]=j;
}
if(str[i][j]=='=')
{
end[0]=i;end[1]=j;
}
}
}
printf("%d\n",bfs());
return 0;
}