【机器学习】聚类（三）：原型聚类：高斯混合聚类

news2024/11/20 0:49:13

文章目录

  • 一、实验介绍
    • 1. 算法流程
    • 2. 算法解释
    • 3. 算法特点
    • 4. 应用场景
    • 5. 注意事项
  • 二、实验环境
    • 1. 配置虚拟环境
    • 2. 库版本介绍
  • 三、实验内容
    • 0. 导入必要的库
    • 1. 全局调试变量
    • 2. 调试函数
    • 3. 高斯密度函数（phi）
    • 4. E步（getExpectation）
    • 5. M步（maximize）
    • 6. 数据缩放函数
    • 7. 初始化参数
    • 8. GMM EM算法函数
    • 9. 主函数
  • 四、代码整合

  高斯混合聚类是一种基于概率模型的聚类方法，采用多个高斯分布的线性组合来表示数据的聚类结构。通过对每个样本的多个高斯分布进行加权组合，该算法能够更灵活地适应不同形状的聚类。

一、实验介绍

1. 算法流程

  1. 初始化：
      初始化高斯混合分布的模型参数，包括每个高斯混合成分的均值向量 μ i \mu_i μi​、协方差矩阵 Σ i \Sigma_i Σi​ 和混合系数 π i \pi_i πi​。

{ ( μ 1 , Σ 1 , π 1 ) , ( μ 2 , Σ 2 , π 2 ) , . . . , ( μ k , Σ k , π k ) } \{(\mu_1, \Sigma_1, \pi_1), (\mu_2, \Sigma_2, \pi_2), ..., (\mu_k, \Sigma_k, \pi_k)\} {(μ1​,Σ1​,π1​),(μ2​,Σ2​,π2​),...,(μk​,Σk​,πk​)}

  1. 迭代过程（EM算法）：

    • Expectation (E) 步骤：
      对于每个样本 X j X_j Xj​ 计算其由各混合成分生成的后验概率 γ i j \gamma_{ij} γij​，表示样本属于第 i i i 个混合成分的概率。

    γ i j = π i ⋅ N ( X j ∣ μ i , Σ i ) ∑ l = 1 k π l ⋅ N ( X j ∣ μ l , Σ l ) \gamma_{ij} = \frac{\pi_i \cdot \mathcal{N}(X_j | \mu_i, \Sigma_i)}{\sum_{l=1}^{k} \pi_l \cdot \mathcal{N}(X_j | \mu_l, \Sigma_l)} γij​=∑l=1k​πl​⋅N(Xj​∣μl​,Σl​)πi​⋅N(Xj​∣μi​,Σi​)​

    • Maximization (M) 步骤：
      更新模型参数：
      • 新均值向量 μ i \mu_i μi​ 的更新： μ i = ∑ j = 1 m γ i j X j ∑ j = 1 m γ i j \mu_i = \frac{\sum_{j=1}^{m} \gamma_{ij} X_j}{\sum_{j=1}^{m} \gamma_{ij}} μi​=∑j=1m​γij​∑j=1m​γij​Xj​​
      • 新协方差矩阵 Σ i \Sigma_i Σi​ 的更新： Σ i = ∑ j = 1 m γ i j ( X j − μ i ) ( X j − μ i ) T ∑ j = 1 m γ i j \Sigma_i = \frac{\sum_{j=1}^{m} \gamma_{ij} (X_j - \mu_i)(X_j - \mu_i)^T}{\sum_{j=1}^{m} \gamma_{ij}} Σi​=∑j=1m​γij​∑j=1m​γij​(Xj​−μi​)(Xj​−μi​)T​
      • 新混合系数 π i \pi_i πi​ 的更新： π i = 1 m ∑ j = 1 m γ i j \pi_i = \frac{1}{m} \sum_{j=1}^{m} \gamma_{ij} πi​=m1​∑j=1m​γij​

  2. 停止条件：
      根据设定的停止条件，比如达到最大迭代轮数或模型参数的变化小于某一阈值。

  3. 簇划分：
      根据得到的后验概率 γ i j \gamma_{ij} γij​ 确定每个样本的簇标记，将样本划入概率最大的簇中。

    C i = { X j ∣ argmax i γ i j , 1 ≤ i ≤ k } C_i = \{X_j | \text{argmax}_i \gamma_{ij}, 1 \leq i \leq k\} Ci​={Xj​∣argmaxi​γij​,1≤i≤k}

  4. 输出：
      返回最终的簇划分 C = { C 1 , C 2 , . . . , C k } C = \{C_1, C_2, ..., C_k\} C={C1​,C2​,...,Ck​}。

  高斯混合聚类采用了迭代优化的方式，通过不断更新均值向量、协方差矩阵和混合系数，使得模型对数据的拟合更好。EM算法的E步骤计算后验概率，M步骤更新模型参数，整个过程不断迭代直至满足停止条件。最后，将每个样本划分到概率最大的簇中。

2. 算法解释

  • 通过EM算法的E步骤，计算每个样本属于每个混合成分的后验概率。
  • 通过EM算法的M步骤，更新每个混合成分的均值向量、协方差矩阵和混合系数，优化模型对数据的拟合。
  • 算法通过迭代过程，不断调整模型参数，使得混合分布更好地刻画数据的分布。

3. 算法特点

  • 通过多个高斯分布的组合，适用于不同形状的聚类结构。
  • 采用EM算法进行迭代优化，灵活适应数据的复杂分布。

4. 应用场景

  • 适用于数据具有多个分布的情况，且每个分布可以用高斯分布来描述。
  • 在图像分割、语音识别等领域广泛应用。

5. 注意事项

  • 初始参数的选择可能影响最终聚类效果，因此需要进行多次运行选择最优结果。
  • 算法对异常值不敏感，但在特定场景下可能需要考虑异常值的处理。

二、实验环境

1. 配置虚拟环境

conda create -n ML python==3.9

conda activate ML

conda install scikit-learn matplotlib

2. 库版本介绍

软件包本实验版本
matplotlib3.5.2
numpy1.21.5
python3.9.13
scikit-learn1.0.2

三、实验内容

0. 导入必要的库

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import multivariate_normal
from sklearn.datasets import load_iris

1. 全局调试变量

DEBUG = True
  • 该变量控制是否在执行过程中打印调试信息。

2. 调试函数

def debug(*args, **kwargs):
    global DEBUG
    if DEBUG:
        print(*args, **kwargs)
  • 用于打印调试信息的函数。在整个代码中都使用了它以进行调试。

3. 高斯密度函数（phi）

def phi(Y, mu_k, cov_k):
    # Check for and handle infinite or NaN values in Y
    norm = multivariate_normal(mean=mu_k, cov=cov_k)
    return norm.pdf(Y)
  • 计算多元高斯分布的概率密度函数。

4. E步（getExpectation）

def getExpectation(Y, mu, cov, alpha):
    N = Y.shape[0]
    K = alpha.shape[0]

    assert N > 1, "There must be more than one sample!"
    assert K > 1, "There must be more than one gaussian model!"

    gamma = np.mat(np.zeros((N, K)))

    prob = np.zeros((N, K))
    for k in range(K):
        prob[:, k] = phi(Y, mu[k], cov[k]) * alpha[k]

    prob = np.mat(prob)

    for k in range(K):
        gamma[:, k] = prob[:, k] / np.sum(prob, axis=1)

    return gamma
  • EM算法的E步骤，计算每个数据点属于每个簇的概率。主要步骤包括：
    • 初始化一个零矩阵 gamma 用于存储响应度。
    • 对于每个簇，计算每个数据点属于该簇的概率（通过 phi 函数计算），然后乘以该簇的混合系数。
    • 归一化概率以得到响应度矩阵 gamma。

5. M步（maximize）

def maximize(Y, gamma):
    N, D = Y.shape
    K = gamma.shape[1]

    mu = np.zeros((K, D))
    cov = []
    alpha = np.zeros(K)

    for k in range(K):
        Nk = np.sum(gamma[:, k])
        mu[k, :] = np.sum(np.multiply(Y, gamma[:, k]), axis=0) / Nk

        diff = Y - mu[k]
        cov_k = np.dot(diff.T, np.multiply(diff, gamma[:, k])) / Nk
        cov_k += 1e-6 * np.identity(D)  # Adding a small value to the diagonal for stability
        cov.append(cov_k)

        alpha[k] = Nk / N

    cov = np.array(cov)
    return mu, cov, alpha
  • EM算法的M步骤，即更新模型参数，主要步骤包括：
    • 初始化均值 mu、协方差矩阵列表 cov 和混合系数 alpha。
    • 对于每个簇，计算新的均值、协方差矩阵和混合系数。均值的更新是通过加权平均计算的，协方差矩阵的更新考虑了数据的权重（响应度），混合系数的更新是每个簇中数据点的权重之和。

6. 数据缩放函数

def scale_data(Y):
    for i in range(Y.shape[1]):
        max_ = Y[:, i].max()
        min_ = Y[:, i].min()
        Y[:, i] = (Y[:, i] - min_) / (max_ - min_)
    debug("Data scaled.")
    return Y
  • 将数据集中的每个特征缩放到 [0, 1] 范围内。

7. 初始化参数

def init_params(shape, K):
    N, D = shape
    mu = np.random.rand(K, D)
    cov = np.array([np.eye(D)] * K)
    alpha = np.array([1.0 / K] * K)
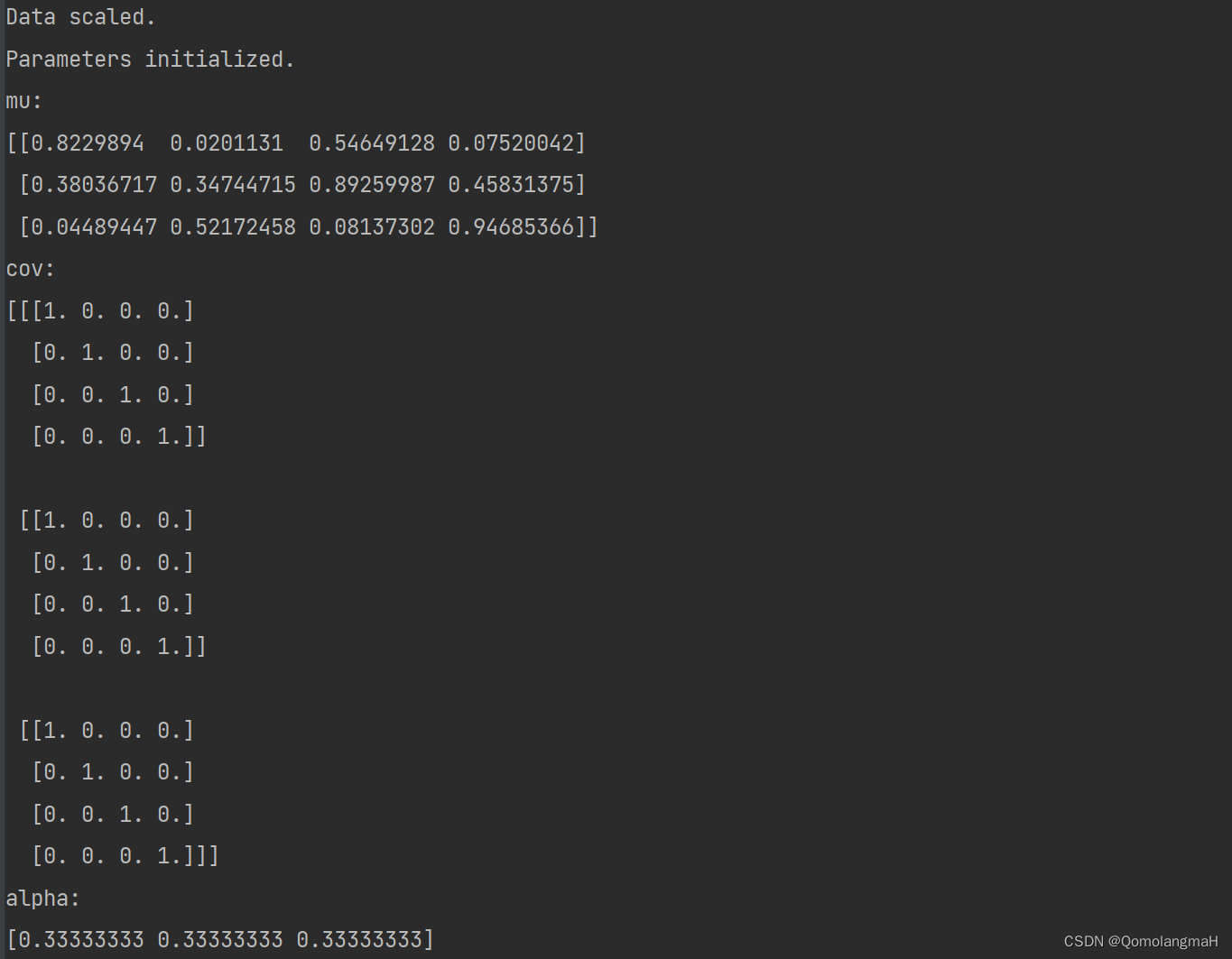
    debug("Parameters initialized.")
    debug("mu:", mu, "cov:", cov, "alpha:", alpha, sep="\n")
    return mu, cov, alpha
  • 初始化GMM的参数（均值、协方差和混合系数）。

在这里插入图片描述

8. GMM EM算法函数

def GMM_EM(Y, K, times):
    Y = scale_data(Y)
    mu, cov, alpha = init_params(Y.shape, K)
    for i in range(times):
        gamma = getExpectation(Y, mu, cov, alpha)
        mu, cov, alpha = maximize(Y, gamma)
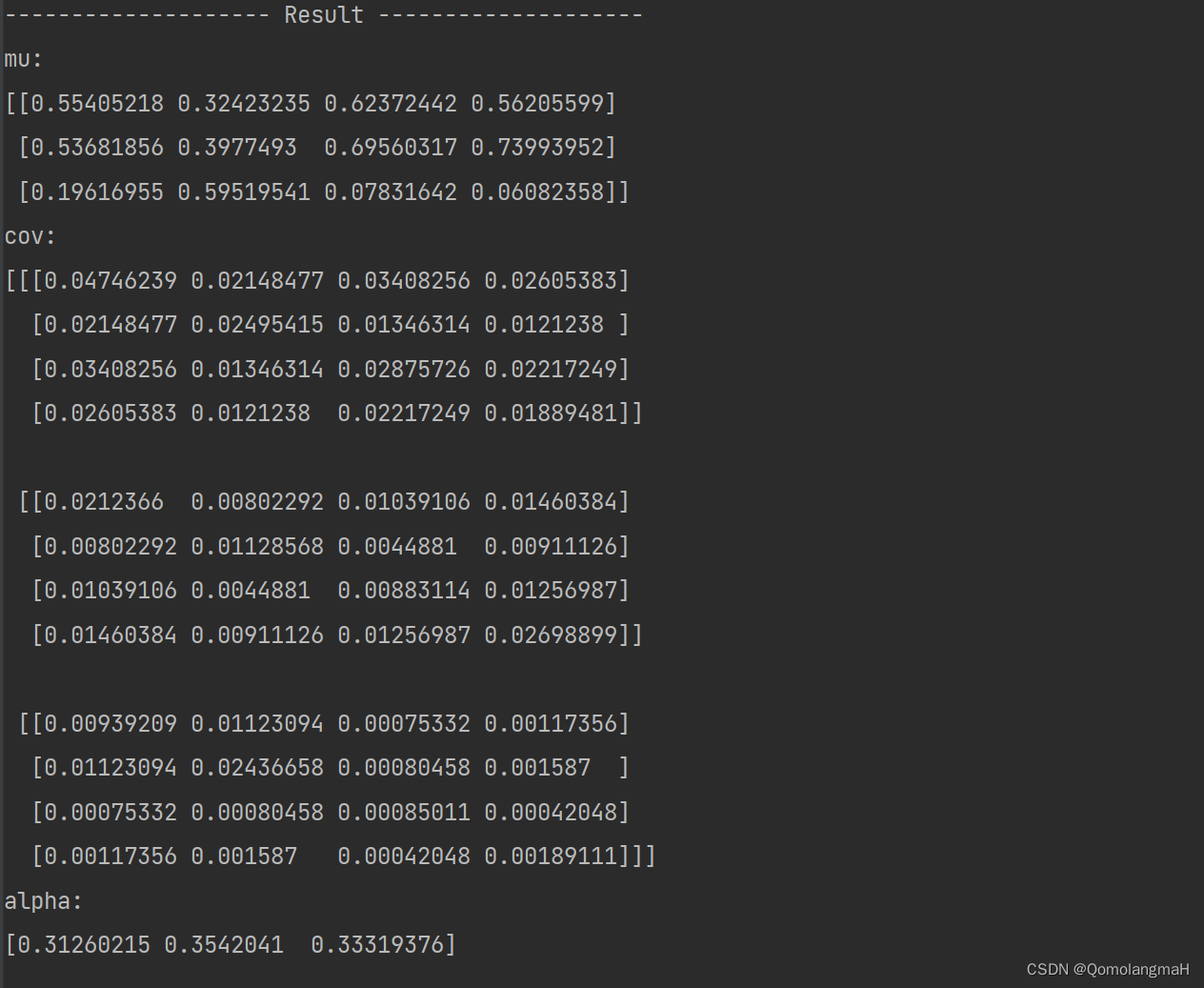
    debug("{sep} Result {sep}".format(sep="-" * 20))
    debug("mu:", mu, "cov:", cov, "alpha:", alpha, sep="\n")
    return mu, cov, alpha

在这里插入图片描述

9. 主函数

if __name__ == '__main__':
    # Load Iris dataset
    iris = load_iris()
    Y = iris.data

    # Model parameters
    K = 3  # number of clusters
    iterations = 100

    # Run GMM EM algorithm
    mu, cov, alpha = GMM_EM(Y, K, iterations)

    # Clustering based on the trained model
    N = Y.shape[0]
    gamma = getExpectation(Y, mu, cov, alpha)
    category = gamma.argmax(axis=1).flatten().tolist()[0]

    # Plotting the results
    for i in range(K):
        cluster_data = np.array([Y[j] for j in range(N) if category[j] == i])
        plt.scatter(cluster_data[:, 0], cluster_data[:, 1], label=f'Cluster {i + 1}')

    plt.legend()
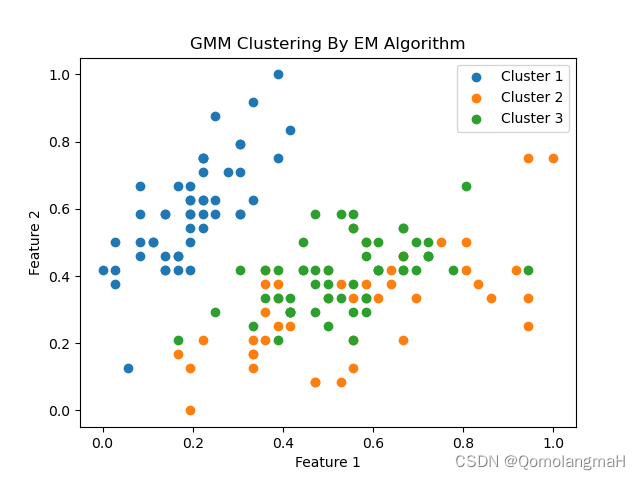
    plt.title("GMM Clustering By EM Algorithm")
    plt.xlabel("Feature 1")
    plt.ylabel("Feature 2")
    plt.show()

在这里插入图片描述

四、代码整合

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import multivariate_normal
from sklearn.datasets import load_iris

DEBUG = True


def debug(*args, **kwargs):
    global DEBUG
    if DEBUG:
        print(*args, **kwargs)


def phi(Y, mu_k, cov_k):
    # Check for and handle infinite or NaN values in Y
    norm = multivariate_normal(mean=mu_k, cov=cov_k)
    return norm.pdf(Y)


def getExpectation(Y, mu, cov, alpha):
    N = Y.shape[0]
    K = alpha.shape[0]

    assert N > 1, "There must be more than one sample!"
    assert K > 1, "There must be more than one gaussian model!"

    gamma = np.mat(np.zeros((N, K)))

    prob = np.zeros((N, K))
    for k in range(K):
        prob[:, k] = phi(Y, mu[k], cov[k]) * alpha[k]

    prob = np.mat(prob)

    for k in range(K):
        gamma[:, k] = prob[:, k] / np.sum(prob, axis=1)

    return gamma


def maximize(Y, gamma):
    N, D = Y.shape
    K = gamma.shape[1]

    mu = np.zeros((K, D))
    cov = []
    alpha = np.zeros(K)

    for k in range(K):
        Nk = np.sum(gamma[:, k])
        mu[k, :] = np.sum(np.multiply(Y, gamma[:, k]), axis=0) / Nk

        diff = Y - mu[k]
        cov_k = np.dot(diff.T, np.multiply(diff, gamma[:, k])) / Nk
        cov_k += 1e-6 * np.identity(D)  # Adding a small value to the diagonal for stability
        cov.append(cov_k)

        alpha[k] = Nk / N

    cov = np.array(cov)
    return mu, cov, alpha



def scale_data(Y):
    for i in range(Y.shape[1]):
        max_ = Y[:, i].max()
        min_ = Y[:, i].min()
        Y[:, i] = (Y[:, i] - min_) / (max_ - min_)
    debug("Data scaled.")
    return Y


def init_params(shape, K):
    N, D = shape
    mu = np.random.rand(K, D)
    cov = np.array([np.eye(D)] * K)
    alpha = np.array([1.0 / K] * K)
    debug("Parameters initialized.")
    debug("mu:", mu, "cov:", cov, "alpha:", alpha, sep="\n")
    return mu, cov, alpha


def GMM_EM(Y, K, times):
    Y = scale_data(Y)
    mu, cov, alpha = init_params(Y.shape, K)
    for i in range(times):
        gamma = getExpectation(Y, mu, cov, alpha)
        mu, cov, alpha = maximize(Y, gamma)
    debug("{sep} Result {sep}".format(sep="-" * 20))
    debug("mu:", mu, "cov:", cov, "alpha:", alpha, sep="\n")
    return mu, cov, alpha


if __name__ == '__main__':
    # Load Iris dataset
    iris = load_iris()
    Y = iris.data

    # Model parameters
    K = 3  # number of clusters
    iterations = 100

    # Run GMM EM algorithm
    mu, cov, alpha = GMM_EM(Y, K, iterations)

    # Clustering based on the trained model
    N = Y.shape[0]
    gamma = getExpectation(Y, mu, cov, alpha)
    category = gamma.argmax(axis=1).flatten().tolist()[0]

    # Plotting the results
    for i in range(K):
        cluster_data = np.array([Y[j] for j in range(N) if category[j] == i])
        plt.scatter(cluster_data[:, 0], cluster_data[:, 1], label=f'Cluster {i + 1}')

    plt.legend()
    plt.title("GMM Clustering By EM Algorithm")
    plt.xlabel("Feature 1")
    plt.ylabel("Feature 2")
    plt.show()

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1252276.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【开源组件】- 关于Jetcache的使用

【开源组件】- 关于Jetcache的使用

关于Jetcache的使用 😄生命不息，写作不止 🔥 继续踏上学习之路，学之分享笔记 👊 总有一天我也能像各位大佬一样 🌝分享学习心得，欢迎指正，大家一起学习成长！ JetCache是由…
阅读更多...
MobileNets发展与总结

MobileNets发展与总结

写在前面：本博客仅作记录学习之用，部分图片来自网络，如需引用请注明出处，同时如有侵犯您的权益，请联系删除！ 文章目录 引言MobileNetsMobileNet - V1思想代码实现 MobileNet - V2思想代码实现 MobileNet - …
阅读更多...
LeetCode Hot100 105.从前序与中序遍历序列构造二叉树

LeetCode Hot100 105.从前序与中序遍历序列构造二叉树

题目&#xff1a;给定两个整数数组 preorder 和 inorder &#xff0c;其中 preorder 是二叉树的先序遍历&#xff0c; inorder 是同一棵树的中序遍历&#xff0c;请构造二叉树并返回其根节点。 代码&#xff1a; class Solution {private Map<Integer, Integer> indexM…
阅读更多...
1.6 C语言之数组概述

1.6 C语言之数组概述

1.6 C语言之数组概述 一、数组二、练习 一、数组 所谓数组&#xff0c;就是内存中一片连续的空间&#xff0c;可以用来存储一组同类型的数据 数组有下标&#xff0c;从0开始&#xff0c;可以理解为是给数组中的元素编号&#xff0c;便于后续寻址访问 我们来编写一个程序&…
阅读更多...
杂货铺 | Windows系统上解压缩tgz文件

杂货铺 | Windows系统上解压缩tgz文件

文章目录 &#x1f4da;快速终端打开实现 & 解压缩实现步骤&#x1f4da;环境变量的一般配置步骤 & 问题解决思路 &#x1f4da;快速终端打开实现 & 解压缩实现步骤 将对应的tgz文件放入对应的文件夹。快速在指定文件夹下打开终端 打开对应的路径 双击地址栏 然后…
阅读更多...
4.28每日一题（二重积分比较大小：被积函数的大小、正负性、积分区间奇偶性）

4.28每日一题（二重积分比较大小：被积函数的大小、正负性、积分区间奇偶性）

一般比较大小的题目我们不需要把结果全部计算出来 &#xff0c;而是通过奇偶性或者被积函数的大小或大于0、等于0、小于0等方法判断比较
阅读更多...
1、Mysql架构与历史

1、Mysql架构与历史

Mysql逻辑架构 最上层是服务并不是Mysql所独有的&#xff0c;大多数基于网络的客户端/服务器的工具或者服务都有类似的架构&#xff0c;比如连接处理&#xff0c;授权认证&#xff0c;安全等。 第二层是Mysql比较有意思的部分。大多数Mysql的核心服务都在这一层&#xff0c;…
阅读更多...
antv/g6的学习总结

antv/g6的学习总结

新建一个简单实例 1、使用命令行在项目目录下执行以下命令 cnpm install --save antv/g6 2、创建容器 <div id"mountNode"></div> 3、在需要用的 G6 的 JS 文件中导入 import G6 from antv/g6; 4、 数据准备 引入 G6 的数据源为 JSON 格式的对象。…
阅读更多...
量化交易：因子风险暴露

量化交易：因子风险暴露

本文介绍了如何计算因子风险暴露的内容。 判断风险暴露的建模是否合理 通常&#xff0c;此分析是基于历史数据&#xff0c;而对历史风险暴露的估计可能会影响未来的风险暴露。 因此&#xff0c;计算因子风险暴露是不够的。 必须对风险暴露保持信心&#xff0c;并明白对风险暴…
阅读更多...
Compose入门

Compose入门

​ 本篇文章主要是为了对Compose有一个初步了解。知道Compose是做什么的&#xff0c;用Compose能干什么&#xff0c;在目前的各种UI框架下面有些优势&#xff0c;参考Google官网的解释加上一些自己的理解生成的一篇文章。本人也是Compose初学者&#xff0c;通过每一步学习遇到哪…
阅读更多...
带你用uniapp从零开发一个仿小米商场_2.创建空白项目及公共样式引入

带你用uniapp从零开发一个仿小米商场_2.创建空白项目及公共样式引入

创建空白项目 打开uniapp 点击新建->项目 如下, 是编辑你项目的名字的地方是你项目存放地址,可以点击浏览器去文件管理里面选地址是模板选择,这里选择默认模板就好是一些其他选择比如uvue能让你项目在编译成软件时运行更快,unicloud能让你用js写后端,且直接就是云开发,g…
阅读更多...
【WSA】无法打开 适用于 Android™ 的 Windows 子系统，因为它处于脱机状态。可能缺少存储设备，或者存储设备已断开连接。

【WSA】无法打开 适用于 Android™ 的 Windows 子系统，因为它处于脱机状态。可能缺少存储设备，或者存储设备已断开连接。

问题描述 之前可以正常使用适用于 Android™ 的 Windows 子系统&#xff08;WSA&#xff09;&#xff0c;但突然间无法启动了。 当尝试启动WSA中的软件时&#xff0c;都会出现以下错误提示&#xff1a; 无法打开 适用于 Android™ 的 Windows 子系统&#xff0c;因为它处于脱…
阅读更多...
基于springboot实现留守儿童爱心网站项目【项目源码+论文说明】计算机毕业设计

基于springboot实现留守儿童爱心网站项目【项目源码+论文说明】计算机毕业设计

基于springboot实现留守儿童爱心网站演示 摘要 随着留守儿童爱心管理的不断发展&#xff0c;留守儿童爱心网站在现实生活中的使用和普及&#xff0c;留守儿童爱心管理成为近年内出现的一个热门话题&#xff0c;并且能够成为大众广为认可和接受的行为和选择。设计留守儿童爱心网…
阅读更多...
数字逻辑电路基础-时序逻辑电路之移位寄存器

数字逻辑电路基础-时序逻辑电路之移位寄存器

文章目录 一、移位寄存器定义二、verilog源码三、仿真结果一、移位寄存器定义 移位寄存器定义 A shift register is a type of digital circuit using a cascade of flip flops where the output of one flip-flop is connected to the input of the next. 移位寄存器是一种将…
阅读更多...
js逆向-某敏感网站登录参数分析

js逆向-某敏感网站登录参数分析

声明 本文仅供学习参考&#xff0c;如有侵权可私信本人删除&#xff0c;请勿用于其他途径&#xff0c;违者后果自负&#xff01; 如果觉得文章对你有所帮助&#xff0c;可以给博主点击关注和收藏哦&#xff01; 前言 目标网站&#xff1a;aHR0cHM6Ly9tZGZnaGcuNXhwb2lqaHRm…
阅读更多...
LED面板显示屏驱动芯片

LED面板显示屏驱动芯片

一、基本概述 TM1638是一种带键盘扫描接口的LED&#xff08;发光二极管显示器&#xff09;驱动控制专用IC,内部集成有MCU数字接口、数据锁存器、LED驱动、键盘扫描等电路。本产品质量可靠、稳定性好、抗干扰能力强。 二、主要应用场合 主要适用于家电设备(智能热水器、微波炉…
阅读更多...
leetcode刷题：17.电话号码的字母组合

leetcode刷题：17.电话号码的字母组合

leetcode原题网页 题目描述&#xff1a;给定一个仅包含数字 2-9 的字符串&#xff0c;返回所有它能表示的字母组合。答案可以按 任意顺序 返回。 给出数字到字母的映射如下&#xff08;与电话按键相同&#xff09;。注意 1 不对应任何字母。 思路&#xff1a;使用vector&#x…
阅读更多...
基于51单片机超市快递寄存自动柜设计源程序

基于51单片机超市快递寄存自动柜设计源程序

一、系统方案 1、本设计采用这51单片机作为主控器。 2、存包&#xff0c;GSM短信取件码。 3、液晶1620显示。 4、矩阵键盘输入取件码&#xff0c;完成取包。 二、硬件设计 原理图如下&#xff1a; 三、单片机软件设计 1、首先是系统初始化 /******************************…
阅读更多...
#BUG SHOW# 深挖一个6年前的老“bug”

#BUG SHOW# 深挖一个6年前的老“bug”

引言 最近参与了一个业务迁移的项目&#xff0c;需要把站点A迁移到站点B。不同的站点拥有各自独立的服务和数据库&#xff0c;可以说是毫无关联。为了兼容迁移过程中的存在的一部分特殊交易数据&#xff08;正向[支付]交易在站点A&#xff0c;但逆向[退款]操作在站点B操作&…
阅读更多...
Oracle 最终抛弃了 Sun ！

Oracle 最终抛弃了 Sun ！

随着 Solaris 团队的彻底完蛋&#xff0c;看起来 Sun 微系统公司最终连块骨头都没剩下。 来自前 Sun 社区的消息表明&#xff0c;一月份的传闻&#xff08;Oracle 裁员 450 人&#xff09;成为了现实&#xff0c;上周五&#xff0c;Oracle 裁掉了 Solaris 和 SPARC 团队的核心员…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023