本文介绍了如何计算因子风险暴露的内容。
判断风险暴露的建模是否合理
通常,此分析是基于历史数据,而对历史风险暴露的估计可能会影响未来的风险暴露。 因此,计算因子风险暴露是不够的。 必须对风险暴露保持信心,并明白对风险暴露的建模是否合理。
运用多因子模型计算因子风险暴露,可以运用多因子模型分析一个组合中风险和收益的来源,多因子模型对收益的分解如下:
![]()
通过对历史收益率进行建模,可以分析出收益中有多少是来自因子收益率,有多少来自资产特质波动(epsilon)。 我们也可以研究投资组合所面临的风险来源,即投资组合的因子暴露。
在风险分析中,我们经常对主动回报(相对于基准的回报)和主动风险(主动回报的标准差,也称为跟踪误差或跟踪风险)进行建模。
例如,我们可计算到一个因子对主动风险的边际贡献——FMCAR。 对于因子j,表示为:
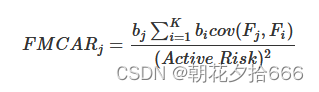
b_j表示组合对因子j的风险暴露,b_i表示组合对因子i的风险暴露,K表示一共K个因子。FMCAR_j这项指标这告诉我们,假设其他条件不变,暴露在因子j下我们增加了多少风险。
策略案例
附件:运用Fama-French三因子模型演示因子风险暴露
# 导入要用到的模块 import numpy as np import statsmodels.api as sm import scipy.stats as stats from statsmodels import regression import matplotlib.pyplot as plt import pandas as pd
获取总市值、总市值排序、市净率、市净率排序、日收益率
start_date = '2016-01-01'
end_date = '2017-05-10'
raw_data = D.features(D.instruments(),start_date,end_date,fields=
['market_cap_0','rank_market_cap_0','pb_lf_0','rank_pb_lf_0','daily_return_0'])
# 每日股票数量
stock_count = raw_data[['date','instrument']].groupby('date').count()
result=raw_data.merge(stock_count.reset_index('date'), on=['date'], how='outer')
result = result.rename(columns={'instrument_x':'instrument','instrument_y':'stock_count'})
我们将市值最小的600只股票记为smallest组,将市值最大的600只股票记为biggest组
我们将市净率最小的600股票记为lowpb组,将市净率最大的600只股票记为highpb组
def is_smallest(x):
if x.rank_market_cap_0 < 600/x.stock_count:
return True
else:
return False
result['smallest'] = result.apply(is_smallest,axis=1)
def is_biggest(x):
if x.rank_market_cap_0 > 1-600/x.stock_count:
return True
else:
return False
result['biggest'] = result.apply(is_biggest,axis=1)
def is_lowpb(x):
if x.rank_pb_lf_0 < 600/x.stock_count:
return True
else:
return False
result['lowpb'] = result.apply(is_lowpb,axis=1)
def is_highpb(x):
if x.rank_pb_lf_0 > 1-600/x.stock_count:
return True
else:
return False
result['highpb'] = result.apply(is_highpb,axis=1)
result = result.set_index('date')
计算每日因子收益率
# 因子收益的定义,以市值因子举例,市值因子收益率=biggest组的平均收益率-smallest组的平均收益率 R_biggest = result[result.biggest]['daily_return_0'].groupby(level=0).mean() R_smallest = result[result.smallest]['daily_return_0'].groupby(level=0).mean() R_highpb = result[result.highpb]['daily_return_0'].groupby(level=0).mean() R_lowpb = result[result.lowpb]['daily_return_0'].groupby(level=0).mean() # 市值因子和市净率因子收益率 SMB = R_smallest - R_biggest HML = R_lowpb - R_highpb
因子累计收益率并绘图
SMB_CUM = np.cumprod(SMB+1)
HML_CUM = np.cumprod(HML+1)
plt.plot(SMB_CUM.index, SMB_CUM.values,)
plt.plot(HML_CUM.index, HML_CUM.values)
plt.ylabel('Cumulative Return')
plt.legend(['SMB Portfolio Returns', 'HML Portfolio Returns']);
计算风险暴露程度
下面我们运用多因素模型和线性回归工具来计算某只股票的回报率相对于这些因子的风险暴露程度。我们以某个资产组合的主动收益作为被解释变量,对因子做回归,一个因子对主动收益贡献越大,那么这个资产组合的主动收益对于该因子的暴露程度也越高。
# 我们以5只股票的组合(portfolio)举例
instruments = D.instruments()[:5]
Stock_matrix = D.history_data(instruments,start_date,end_date,fields=['close'])
Stock_matrix = pd.pivot_table(Stock_matrix,values='close',index=['date'],columns=['instrument'])
portfolio = Stock_matrix.pct_change()[1:]
# 组合的每日收益率(等权重组合)
R = np.mean(portfolio, axis=1)
# 基准收益率
bench = D.history_data('000300.SHA',start_date, end_date, fields=['close']).set_index('date')['close'].pct_change()[1:]
# 主动收益率
active = R - bench
# 建立一个常数项,为下文回归做准备
constant = pd.TimeSeries(np.ones(len(active.index)), index=active.index)
df = pd.DataFrame({'R': active,
'F1': SMB,
'F2': HML,
'Constant': constant})
# 删除含有缺失值的行
df = df.dropna()
线性回归并获取回归系数
b1, b2 = regression.linear_model.OLS(df['R'], df[['F1', 'F2']]).fit().params
# 因子对于主动收益的敏感性(即因子暴露)
print('Sensitivities of active returns to factors:\nSMB: %f\nHML: %f' % (b1, b2))
边际贡献
利用前文中的公式,计算因子对主动收益风险平方的边际贡献(factors' marginal contributions to active risk squared,FMCAR )
# 计算因子风险贡献
F1 = df['F1']
F2 = df['F2']
cov = np.cov(F1, F2)
ar_squared = (active.std())**2
fmcar1 = (b1*(b2*cov[0,1] + b1*cov[0,0]))/ar_squared
fmcar2 = (b2*(b1*cov[0,1] + b2*cov[1,1]))/ar_squared
print('SMB Risk Contribution:', fmcar1)
print('HML Risk Contribution:', fmcar2)
余下的风险可以归结于一些特有的风险因素,即我们没有加入模型的因子或者资产组合本身独有的某种风险。 通常我们会关注一下对这些因子的风险暴露随时间如何变化。让我们rolling一下~
# 计算滚动的beta
model = pd.stats.ols.MovingOLS(y = df['R'], x=df[['F1', 'F2']],
window_type='rolling',
window=100)
rolling_parameter_estimates = model.beta
rolling_parameter_estimates.plot()
plt.title('Computed Betas');
plt.legend(['F1 Beta', 'F2 Beta', 'Intercept']);
现在我们来看看FMCAR是如何随时间变化的
# 计算方差协方差
# 去除有缺省值的日期,从有实际有效值的日期开始
covariances = pd.rolling_cov(df[['F1', 'F2']], window=100)[99:]
# 计算主动风险
active_risk_squared = pd.rolling_std(active, window = 100)[99:]**2
# 计算beta
betas = rolling_parameter_estimates[['F1', 'F2']]
# 新建一个空的dataframe
FMCAR = pd.DataFrame(index=betas.index, columns=betas.columns)
# 每个因子循环
for factor in betas.columns:
# 每一天循环
for t in betas.index:
# 求beta与协方差之积的和,见公式
s = np.sum(betas.loc[t] * covariances[t][factor])
# 获取beta
b = betas.loc[t][factor]
# 获取主动风险
AR = active_risk_squared.loc[t]
# 估计当天的FMCAR
FMCAR[factor][t] = b * s / AR
因子对于主动收益风险的边际贡献
plt.plot(FMCAR['F1'].index, FMCAR['F1'].values)
plt.plot(FMCAR['F2'].index, FMCAR['F2'].values)
plt.ylabel('Marginal Contribution to Active Risk Squared')
plt.legend(['F1 FMCAR', 'F2 FMCAR'])
存在的问题
了解历史数据中组合对各个因子的暴露程度是很有趣的,但只有将它用在对未来预测上时,它才有用武之地。但我们不是总能够放心地认为未来的情况与现在相同,由于随时间会变化,对风险暴露程度取平均值也很容易出现问题。我们可以给均值加上一个置信区间,但只有当其分布是正态分布或者表现很稳健才行。我们来看看Jarque-Bera测验的结果。
from statsmodels.stats.stattools import jarque_bera
_, pvalue1, _, _ = jarque_bera(FMCAR['F1'].dropna().values)
_, pvalue2, _, _ = jarque_bera(FMCAR['F2'].dropna().values)
print('p-value F1_FMCAR is normally distributed', pvalue1)
print('p-value F2_FMCAR is normally distributed', pvalue2)
p_value显示我们可以显著的拒绝其为正态分布,可见对于未来这些因素会导致多少风险暴露是很难估计的,所以在使用这些统计模型去估计风险暴露并以此为依据来对冲是需要万分小心的。





![Halcon [fill_up_shape],[close_circle],[dilation_circle]和[shape_trans]图像处理时填充区别](https://img-blog.csdnimg.cn/26b37f1895af4e3ebff0e9ed2031adaf.png)