文章目录
- 整体
- 文字提炼
- 图像绘画
- 考点
- 记忆/考点汇总——按大纲
本篇思路:根据各方的资料,比如名师的资料,按大纲或者其他方式,收集/汇总考点,即需记忆点,在通过整体的记忆法,比如整体信息很多,通常使用记忆宫殿法,绘图记忆法进行记忆,针对局部/细节/组成的部分,可通过多种方法,比如联想记忆法、理解记忆法等进行进一步记忆。
整体
整体使用记忆宫殿法和绘图记忆法等进行记忆
文字提炼
通过目录大纲法和重点归纳法等,进行重要考点的提炼串联
函数、方程、不等式:【函数核心在于图像,图像又涉及交点;方程核心在于根】
第一:从一元二次函数、方程、不等式出发(因为三者知识点最多且互有关联)
1.对于一元二次函数:
【固定做题法:
⟹
\Longrightarrow
⟹ 一看开口方向:(注意自然语言的表达以决定对二次项系数a是否等于0进行分类讨论)二次函数,二次方程,二次不等式,抛物线(默认a≠0);函数,方程,不等式(需要对a是否等于0进行分类讨论)
⟹
\Longrightarrow
⟹ 二看判别式:
△
=
b
2
−
4
a
c
△=b^2-4ac
△=b2−4ac
⟹
\Longrightarrow
⟹ 三看对称轴:
x
=
−
b
2
a
x=-\frac{b}{2a}
x=−2ab
⟹
\Longrightarrow
⟹ 四看交点值:顶点坐标:
(
−
b
2
a
,
4
a
c
−
b
2
4
a
)
(-\frac{b}{2a},\frac{4ac-b^2}{4a})
(−2ab,4a4ac−b2)。当
△
=
b
2
−
4
a
c
>
0
△=b^2-4ac>0
△=b2−4ac>0时,函数图象与x轴有两个不同的交点
M
1
(
x
1
,
0
)
,
M
2
(
x
2
,
0
)
M_1(x_1,0),M_2(x_2,0)
M1(x1,0),M2(x2,0),则
∣
M
1
M
2
∣
=
∣
x
1
−
x
2
∣
=
△
∣
a
∣
|M_1M_2|=|x_1-x_2|=\frac{\sqrt{△}}{|a|}
∣M1M2∣=∣x1−x2∣=∣a∣△。
】
图像绘画
记忆宫殿法的记忆桩来存放一二级目录,绘图记忆法记忆细节等。
床尾游泳池
U型泳池放置一元二次函数
泳池上部分:有颗苹果
泳池下部:有着顶点,一边是对称轴,一边是y最值。
考点
通过汇总各方大佬资料,作为收集考点/记忆点的信息输入:XX,收集汇总如下:
汇总考点的必要,或者说,汇总记忆的内容的必要,不言而喻,首先,你要记忆东西,得有东西,所以你要梳理出你需要记忆的全部东西,其次,在收集多个大佬的梳理的考点,又可以找出各条逻辑帮助记忆考点,所以,梳理考点是很有必要的,是记忆的基础,是记忆宫殿里面的物品,是我们最后考试需要去找到的解题物品。
记忆/考点汇总——按大纲
——一元二次函数——【图像→交点】
——【
a
x
2
+
b
x
+
c
=
y
ax^2+bx+c=y
ax2+bx+c=y二次函数核心在于“图像”:整体可以由: 图像(形状,上下,交点)
⟹
\Longrightarrow
⟹
△
△
△
⟹
\Longrightarrow
⟹ 抛物线与x轴交点
⟹
\Longrightarrow
⟹ 交点图形】
——【固定做题法:
⟹
\Longrightarrow
⟹ 一看开口方向:(注意自然语言的表达以决定对二次项系数a是否等于0进行分类讨论)二次函数,二次方程,二次不等式,抛物线(默认a≠0);函数,方程,不等式(需要对a是否等于0进行分类讨论)
⟹
\Longrightarrow
⟹ 二看判别式:
△
=
b
2
−
4
a
c
△=b^2-4ac
△=b2−4ac
⟹
\Longrightarrow
⟹ 三看对称轴:
x
=
−
b
2
a
x=-\frac{b}{2a}
x=−2ab
⟹
\Longrightarrow
⟹ 四看交点值:顶点坐标:
(
−
b
2
a
,
4
a
c
−
b
2
4
a
)
(-\frac{b}{2a},\frac{4ac-b^2}{4a})
(−2ab,4a4ac−b2)。当
△
=
b
2
−
4
a
c
>
0
△=b^2-4ac>0
△=b2−4ac>0时,函数图象与x轴有两个不同的交点
M
1
(
x
1
,
0
)
,
M
2
(
x
2
,
0
)
M_1(x_1,0),M_2(x_2,0)
M1(x1,0),M2(x2,0),则
∣
M
1
M
2
∣
=
∣
x
1
−
x
2
∣
=
△
∣
a
∣
|M_1M_2|=|x_1-x_2|=\frac{\sqrt{△}}{|a|}
∣M1M2∣=∣x1−x2∣=∣a∣△。】
1.三种函数形式:
一般式:
y
=
a
x
2
+
b
x
+
c
(
a
≠
0
)
y=ax^2+bx+c(a≠0)
y=ax2+bx+c(a=0)
配方式/顶点式:
y
=
a
(
x
+
b
2
a
)
2
+
4
a
c
−
b
2
4
a
y=a(x+\frac{b}{2a})^2+\frac{4ac-b^2}{4a}
y=a(x+2ab)2+4a4ac−b2,对称轴为
x
=
−
b
2
a
x=-\frac{b}{2a}
x=−2ab,顶点坐标为
(
−
b
2
a
,
4
a
c
−
b
2
4
a
)
(-\frac{b}{2a},\frac{4ac-b^2}{4a})
(−2ab,4a4ac−b2)
两根/零点式:
y
=
a
(
x
−
x
1
)
(
x
−
x
2
)
y=a(x-x_1)(x-x_2)
y=a(x−x1)(x−x2),
x
1
,
x
2
x_1,x_2
x1,x2是函数的两个根,对称轴为
x
=
x
1
+
x
2
2
x=\frac{x_1+x_2}{2}
x=2x1+x2
2.图像特点:
图像形状:二次函数
y
=
a
x
2
+
b
x
+
c
(
a
≠
0
)
y=ax^2+bx+c(a≠0)
y=ax2+bx+c(a=0)的图像是一条抛物线。——【图像的全身】
开口方向:由a决定,当a>0时,抛物线开口向上;当a<0时,抛物线开口向下。——【图像的嘴巴】
对称轴:以
x
=
−
b
2
a
x=-\frac{b}{2a}
x=−2ab为对称轴。——【图像的比例】
顶点坐标:
(
−
b
2
a
,
4
a
c
−
b
2
4
a
)
(-\frac{b}{2a},\frac{4ac-b^2}{4a})
(−2ab,4a4ac−b2)。——【图像的头部】
y轴截距:c,c决定抛物线与y轴交点的位置,影响顶点高度。
定义域:一般隐藏在判别式大于等于零中。
最值:当a>0(a<0)时,有最小(大)值
4
a
c
−
b
2
4
a
\frac{4ac-b^2}{4a}
4a4ac−b2,无最大(小)值。——【需验证对称轴是否在定义域内,在则可套用顶点坐标求最值】
单调性:当a>0时,抛物线开口向上,函数在
(
−
∞
,
−
b
2
a
]
(-∞,-\frac{b}{2a}]
(−∞,−2ab]上递减,在
[
−
b
2
a
,
+
∞
)
[-\frac{b}{2a},+∞)
[−2ab,+∞)上递增,当
x
=
−
b
2
a
x=-\frac{b}{2a}
x=−2ab时,
f
(
x
)
m
i
n
=
4
a
c
−
b
2
4
a
f(x)_{min}=\frac{4ac-b^2}{4a}
f(x)min=4a4ac−b2;当
a
<
0
a<0
a<0时,抛物线开口向下,函数在
(
−
∞
,
−
b
2
a
]
(-∞,-\frac{b}{2a}]
(−∞,−2ab]上递增,在
[
−
b
2
a
,
+
∞
)
[-\frac{b}{2a},+∞)
[−2ab,+∞)上递减,当
x
=
−
b
2
a
x=-\frac{b}{2a}
x=−2ab时,
f
(
x
)
m
a
x
=
4
a
c
−
b
2
4
a
f(x)_{max}=\frac{4ac-b^2}{4a}
f(x)max=4a4ac−b2。——【】
交点图像:当
△
=
b
2
−
4
a
c
>
0
△=b^2-4ac>0
△=b2−4ac>0时,函数图象与x轴有两个不同的交点
M
1
(
x
1
,
0
)
,
M
2
(
x
2
,
0
)
M_1(x_1,0),M_2(x_2,0)
M1(x1,0),M2(x2,0),则
∣
M
1
M
2
∣
=
∣
x
1
−
x
2
∣
=
△
∣
a
∣
|M_1M_2|=|x_1-x_2|=\frac{\sqrt{△}}{|a|}
∣M1M2∣=∣x1−x2∣=∣a∣△。——【图像的内部】
3.参数含义:二次函数
y
=
a
x
2
+
b
x
+
c
(
a
≠
0
)
y=ax^2+bx+c(a≠0)
y=ax2+bx+c(a=0)
a:当a>0(a<0)时,有最小(大)值
4
a
c
−
b
2
4
a
\frac{4ac-b^2}{4a}
4a4ac−b2,无最大(小)值。
b:影响对称轴位置,因以
x
=
−
b
2
a
x=-\frac{b}{2a}
x=−2ab为对称轴。——【a,b决定对称轴的位置】
c:代表图像在y轴上的截距(纵截距),影响顶点高度,因顶点坐标为
(
−
b
2
a
,
4
a
c
−
b
2
4
a
)
(-\frac{b}{2a},\frac{4ac-b^2}{4a})
(−2ab,4a4ac−b2)。
4.图像与x轴的位置:
已知函数
y
=
a
x
2
+
b
x
+
c
y=ax^2+bx+c
y=ax2+bx+c与x轴交点的个数,可知
(1)若函数与x轴有2个交点,则
a
≠
0
和△
=
b
2
−
4
a
c
>
0
a≠0和△=b^2-4ac>0
a=0和△=b2−4ac>0;——【【易错点】此类题易忘掉一元二次函数(方程、不等式)的二次项系数不能为0。要使用
△
=
b
2
−
4
a
c
△=b^2-4ac
△=b2−4ac,必先看二次项系数是否为0。】
(2)若函数与x轴有1个交点,即抛物线与x轴相切或图像是一条直线,则
a
≠
0
和△
=
b
2
−
4
a
c
=
0
a≠0和△=b^2-4ac=0
a=0和△=b2−4ac=0;或
a
=
0
和
b
≠
0
a=0和b≠0
a=0和b=0;
(3)若函数与轴没有交点,则
a
≠
0
和△
=
b
2
−
4
a
c
<
0
a≠0和△=b^2-4ac<0
a=0和△=b2−4ac<0或
a
=
b
=
0
和
c
≠
0
a=b=0和c≠0
a=b=0和c=0。
(4)图像始终位于x轴上方,则
a
>
0
和△
=
b
2
−
4
a
c
<
0
a>0和△=b^2-4ac<0
a>0和△=b2−4ac<0
(5)图像始终位于x轴下方,则
a
<
0
和△
=
b
2
−
4
a
c
<
0
a<0和△=b^2-4ac<0
a<0和△=b2−4ac<0
5.图像与一次函数的交点:
二次函数
y
=
a
x
2
+
b
x
+
c
y=ax^2+bx+c
y=ax2+bx+c与一次函数
y
=
k
x
+
m
y=kx+m
y=kx+m的交点情况有三种,利用数形结合思想,令两函数值相等,得到新的一元二次方程
a
x
2
+
b
x
+
c
−
(
k
x
+
m
)
=
0
ax^2+bx+c-(kx+m)=0
ax2+bx+c−(kx+m)=0。
(1)2个交点:新的一元二次方程
△>
0
△>0
△>0。
(2)1个交点:①一次函数与二次函致相切,新的一元二次方程
△
=
0
△=0
△=0。特别地,在顶点处相切时,
k
=
0
k=0
k=0,一次函数为
y
=
4
a
c
−
b
2
4
a
y=\frac{4ac-b^2}{4a}
y=4a4ac−b2。②一次函数垂直于x轴,k不存在。
(3)0个交点:新的一元二次方程
△<
0
△<0
△<0。
6.特殊的抛物线
y
=
a
x
2
+
b
x
+
c
(
a
≠
0
)
y=ax^2+bx+c(a≠0)
y=ax2+bx+c(a=0)
(1)若
b
=
0
b= 0
b=0,则
y
=
a
x
2
+
c
y=ax^2+c
y=ax2+c,抛物线的对称轴为y轴。
(2)若c = 0,则
y
=
a
x
2
+
b
x
y=ax^2+bx
y=ax2+bx,抛物线过原点。
(3)若
b
=
c
=
0
b=c=0
b=c=0,则
y
=
a
x
2
y= ax^2
y=ax2,抛物线的对称轴为y轴且过原点。
——其他函数——【记图像可辅助记忆性质】
正比例函数:
y
=
k
x
(
k
≠
0
)
y=kx(k≠0)
y=kx(k=0),定义域为
R
R
R,值域为
R
R
R,单调性为
k
>
0
k>0
k>0时,单调递增;
k
<
0
k<0
k<0时,单调递减,图像是“一条直线”。
反比例函数:
y
=
k
x
(
k
为常数,
k
≠
0
)
y=\frac{k}{x}(k为常数,k≠0)
y=xk(k为常数,k=0),定义域为{
x
∣
x
≠
0
x|x≠0
x∣x=0},单调性为k>0时,在区间
(
−
∞
,
0
)
,
(
0
,
+
∞
)
(-∞,0),(0,+∞)
(−∞,0),(0,+∞)上单调递减;k<0时,在区间
(
−
∞
,
0
)
,
(
0
,
+
∞
)
(-∞,0),(0,+∞)
(−∞,0),(0,+∞)上单调递增,值域为{
y
∣
y
≠
0
y|y≠0
y∣y=0},图像是“两条圆心对称的圆弧”。
对勾函数:
y
=
x
+
1
x
y=x+\frac{1}{x}
y=x+x1,定义域为{
x
∣
x
≠
0
x|x≠0
x∣x=0},值域为
(
−
∞
,
−
2
)
∪
(
2
,
+
∞
)
(-∞,-2)∪(2,+∞)
(−∞,−2)∪(2,+∞),单调性为在区间
(
−
∞
,
−
1
)
,
(
1
,
+
∞
)
(-∞,-1),(1,+∞)
(−∞,−1),(1,+∞)上单调递增;在区间
(
−
1
,
0
)
,
(
0
,
1
)
(-1,0),(0,1)
(−1,0),(0,1)上单调递减,图像是“两条圆心对称的耐特勾”。
指数函数:
y
=
a
x
(
a
>
0
,
a
≠
1
)
y=a^x(a>0,a≠1)
y=ax(a>0,a=1),定义域为
(
−
∞
,
+
∞
)
(-∞,+∞)
(−∞,+∞),值域
(
0
,
+
∞
)
(0,+∞)
(0,+∞),单调性为当
a
>
1
a>1
a>1时,是增函数;当
0
<
a
<
1
0<a<1
0<a<1时,是减函数。图像恒过点
(
0
,
1
)
,是“一条弧线”
(0,1),是“一条弧线”
(0,1),是“一条弧线”。——【
a
>
0
a>0
a>0和
0
<
a
<
1
0<a<1
0<a<1两图像形成交叉于
(
0
,
1
)
(0,1)
(0,1)的文字yi乂】——【指数函数的重点有两部分,一部分是图像性质,往往会涉及利用单调性比大小。另一部分是运算性质,考生需要牢记指数函数的运算公式。】
对数函数:
y
=
l
o
g
a
x
(
a
>
0
且
a
≠
1
)
y=log_ax(a>0且a≠1)
y=logax(a>0且a=1),定义域为
(
0
,
+
∞
)
(0,+∞)
(0,+∞),值域
全体实数
R
全体实数R
全体实数R,单调性为当
a
>
1
a>1
a>1时,是增函数;当
0
<
a
<
1
0<a<1
0<a<1时,是减函数。图像恒过点
(
1
,
0
)
,是“一条弧线”
(1,0),是“一条弧线”
(1,0),是“一条弧线”。它与
y
=
a
x
y=a^x
y=ax互为反函数。——【
a
>
0
a>0
a>0和
0
<
a
<
1
0<a<1
0<a<1两图像形成交叉于
(
1
,
0
)
(1,0)
(1,0)的躺着的文字yi乂】——【对数函数的重点有两部分,一部分是图像性质,往往会涉及利用单调性比大小。另一部分是运算性质,考生需要牢记对数函数的运算公式。此外,对数函数有一个最容易设置陷阱的地方就是在对数函数中要求真数部分恒大于0。】
反函数:同底的指数函数
y
=
a
x
y=a^x
y=ax与对数函数
y
=
l
o
g
a
x
y=log_ax
y=logax互为反函数。
指数运算:
a
m
⋅
a
n
=
a
m
+
n
a^m·a^n=a^{m+n}
am⋅an=am+n;
a
m
÷
a
n
=
a
m
−
n
a^m÷a^n=a^{m-n}
am÷an=am−n;
(
a
m
)
n
=
a
m
n
(a^m)n=a^{mn}
(am)n=amn;
a
0
=
1
a^0=1
a0=1;
a
−
n
=
1
a
n
a^{-n}=\frac{1}{a^n}
a−n=an1;
a
m
n
=
a
m
n
a^{\frac{m}{n}}=\sqrt[n]{a^m}
anm=nam——【指数函数重点=图像+运算】
对数运算:当
a
>
0
a>0
a>0且
a
≠
1
a≠1
a=1时,
m
>
0
m>0
m>0,
n
>
0
n>0
n>0,则
l
o
g
底
真
log_底真
log底真:——【乘除变加减,指数提到前】
指对互换:
a
b
=
N
a^b=N
ab=N
⟺
\Longleftrightarrow
⟺
l
o
g
a
N
=
b
(
a
>
0
,
a
≠
1
,
N
>
0
)
log_aN=b(a>0,a≠1,N>0)
logaN=b(a>0,a=1,N>0)
同底对数:
l
o
g
a
M
+
l
o
g
a
N
=
l
o
g
a
(
M
N
)
log_aM+log_aN=log_a(MN)
logaM+logaN=loga(MN);
同底对数:
l
o
g
a
M
−
l
o
g
a
N
=
l
o
g
a
(
M
N
)
log_aM-log_aN=log_a(\frac{M}{N})
logaM−logaN=loga(NM);
幂运算:
l
o
g
a
m
b
n
=
n
m
l
o
g
a
b
log_{a^m}b^n=\frac{n}{m}log_ab
logambn=mnlogab;
m
=
1
m=1
m=1时,
l
o
g
a
b
n
=
n
l
o
g
a
b
log_ab^n=nlog_ab
logabn=nlogab;
m
=
n
m=n
m=n时,
l
o
g
a
m
b
n
=
l
o
g
a
b
log_{a^m}b^n=log_ab
logambn=logab;
l
o
g
a
M
n
=
1
n
l
o
g
a
M
log_a\sqrt[n]{M}=\frac{1}{n}log_aM
loganM=n1logaM;
换底公式:
l
o
g
a
b
=
l
o
g
c
b
l
o
g
c
a
=
l
g
b
l
g
a
=
l
n
b
l
n
a
log_ab=\frac{log_cb}{log_ca}=\frac{lgb}{lga}=\frac{lnb}{lna}
logab=logcalogcb=lgalgb=lnalnb,
l
o
g
a
b
=
1
l
o
g
b
a
log_ab=\frac{1}{log_ba}
logab=logba1,
l
o
g
a
M
=
l
o
g
b
M
÷
l
o
g
b
a
(
b
>
0
且
b
≠
1
)
log_aM=log_bM÷log_ba(b>0且b≠1)
logaM=logbM÷logba(b>0且b=1),一般c取10或e。——【换底公式,真数在上,底数在下】
常用对数:以10为底的对数,
l
o
g
10
N
log_{10}N
log10N,简记为
l
g
N
lgN
lgN;
自然对数:以无理数e(e=2.71828…)为底的对数,
l
o
g
e
N
log_eN
logeN,简记为
l
n
N
lnN
lnN。
特殊对数:
l
o
g
a
1
=
0
log_a1=0
loga1=0,
l
o
g
a
a
=
1
log_aa=1
logaa=1,
l
o
g
a
b
⋅
l
o
g
b
a
=
1
log_ab·log_ba=1
logab⋅logba=1,负数和零没有对数,
a
l
o
g
a
b
=
b
a^{log_ab}=b
alogab=b,
l
o
g
a
a
s
=
s
log_aa^s=s
logaas=s——【
a
l
o
g
a
b
=
b
a^{log_ab}=b
alogab=b】
最值函数:
最大值函数:
m
a
x
max
max{
x
,
y
,
z
x,y,z
x,y,z}表示
x
,
y
,
z
x,y,z
x,y,z中最大的数;本质为:
m
a
x
max
max{
a
,
b
,
c
a,b,c
a,b,c}
≥
a
≥a
≥a且
m
a
x
max
max{
a
,
b
,
c
a,b,c
a,b,c}
≥
b
≥b
≥b且
m
a
x
max
max{
a
,
b
,
c
a,b,c
a,b,c}
≥
c
≥c
≥c。对于函数而言,
m
a
x
max
max{
f
(
x
)
,
g
(
x
)
f(x),g(x)
f(x),g(x)}表示各函数图像中最高的部分。
最小值函数:
m
i
n
min
min{
x
,
y
,
z
x,y,z
x,y,z}表示
x
,
y
,
z
x,y,z
x,y,z中最小的数。本质为:
m
i
n
min
min{
a
,
b
,
c
a,b,c
a,b,c}
≤
a
≤a
≤a且
m
i
n
min
min{
a
,
b
,
c
a,b,c
a,b,c}
≤
b
≤b
≤b且
m
i
n
min
min{
a
,
b
,
c
a,b,c
a,b,c}
≤
c
≤c
≤c。对于函数而言,
m
i
n
min
min{
f
(
x
)
,
g
(
x
)
f(x),g(x)
f(x),g(x)}表示各函数图像中最低的部分。
对于max函数图像,先画出各函数图像,然后取图像位于上方部分;对于min函数图像,先画出各函数图像,然后取图像位于下方部分。
绝对值函数:
y
=
∣
a
x
+
b
∣
y=|ax+b|
y=∣ax+b∣先画
y
=
a
x
+
b
y=ax+b
y=ax+b的图像,再将x轴下方的图像翻到x轴上方。
y
=
∣
a
x
2
+
b
x
+
c
∣
y=|ax^2+bx+c|
y=∣ax2+bx+c∣的图像,再将x轴下方的图像翻到x轴上方。
y
=
a
x
2
+
b
∣
x
∣
+
c
y=ax^2+b|x|+c
y=ax2+b∣x∣+c先画
y
=
a
x
2
+
b
x
+
c
y=ax^2+bx+c
y=ax2+bx+c的图像,再将y轴左侧图像删掉,替换成y轴右侧对称过来的图像。
∣
a
x
+
b
y
∣
=
c
b
|ax+by|=cb
∣ax+by∣=cb表示两条平行的直线
a
x
+
b
y
=
±
c
ax+by=±c
ax+by=±c,且两者关于原点对称。
∣
a
x
∣
+
∣
b
y
∣
=
c
|ax|+|by|=c
∣ax∣+∣by∣=c,当
a
=
b
a=b
a=b时,表示正方形,当
a
≠
b
a≠b
a=b时,表示菱形。
∣
x
y
∣
+
a
b
=
a
∣
x
∣
+
b
∣
y
∣
|xy|+ab=a|x|+b|y|
∣xy∣+ab=a∣x∣+b∣y∣,
∣
x
y
∣
+
a
b
=
a
∣
x
∣
+
b
∣
y
∣
|xy|+ab=a|x|+b|y|
∣xy∣+ab=a∣x∣+b∣y∣
⟹
\Longrightarrow
⟹
∣
x
y
∣
−
a
∣
x
∣
−
b
∣
y
∣
+
a
b
=
0
|xy|-a|x|-b|y|+ab=0
∣xy∣−a∣x∣−b∣y∣+ab=0
⟹
\Longrightarrow
⟹
∣
x
∣
(
∣
y
∣
−
a
)
−
b
(
∣
y
∣
−
a
)
=
0
|x|(|y|-a)-b(|y|-a)=0
∣x∣(∣y∣−a)−b(∣y∣−a)=0
⟹
\Longrightarrow
⟹
(
∣
x
∣
−
b
)
(
∣
y
∣
−
a
)
=
0
(|x|-b)(|y|-a)=0
(∣x∣−b)(∣y∣−a)=0
⟹
\Longrightarrow
⟹
∣
x
∣
=
b
|x|=b
∣x∣=b或
∣
y
∣
=
a
|y|=a
∣y∣=a, 故表示由
x
=
±
b
,
y
=
±
a
x=±b,y=±a
x=±b,y=±a围成的图形,当
a
=
b
a=b
a=b时,表示正方形,当
a
≠
b
a≠b
a=b时,表示矩形。
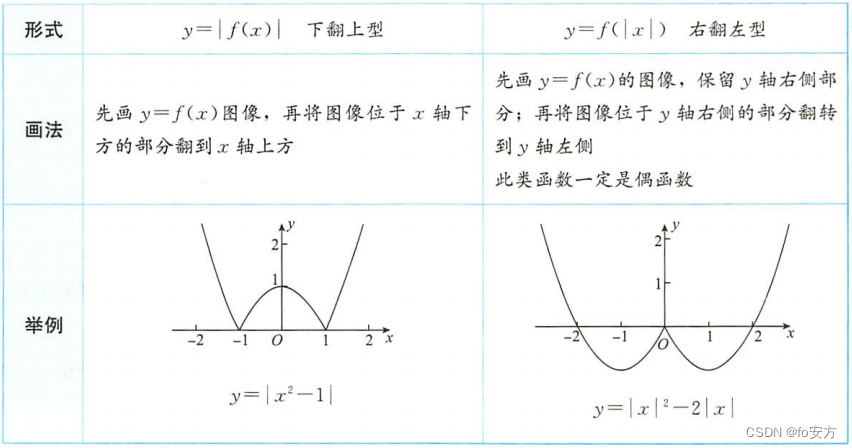
y
=
∣
f
(
x
)
∣
y=|f(x)|
y=∣f(x)∣上翻下型:先画
y
=
f
(
x
)
y=f(x)
y=f(x)图像,再将图像位于x轴下方的部分翻到x轴上方。
y
=
f
(
∣
x
∣
)
y=f(|x|)
y=f(∣x∣)右翻左型:先画
y
=
f
(
x
)
y=f(x)
y=f(x)的图像,保留y轴右侧部分;再将右侧的部分翻转到y轴左侧。
分段函数:
分段函数:对于其定义域内的自变量x的不同值,不能用一个统一的解析式表示,而是要用两个或两个以上的式子表示。分段函数表示不同的取值范围对应不同的表达式。对于分段函数,根据不同取值区间,选择不同的表达式代入求解。
模型识别:自变量在不同取值范围内有不同的对应法则。
解题方法:求分段函数的函数值
f
(
x
0
)
f(x_0)
f(x0)时,应该首先判断
x
0
x_0
x0所属的取值范围,然后把
x
0
x_0
x0代入到相应的解析式中进行计算。
思路:分段函数是指自变量在两个或两个以上不同的范围内,有不同的对应法则的函数。它是一个函数,是一类表达形式特殊的函数,却又常常被学生误认为是几个函数。它的定义城是各段函数定义域的并集,其值域也是各段函数值城的并集。分段函数有关问题蕴含着分类讨论、数形结合等思想方法。分段函数应用较广,做题时要根据范围来确定对应的表达式。
复合函数:
(1)定义:已知函数
y
=
f
(
u
)
y=f(u)
y=f(u),又
u
=
g
(
x
)
u=g(x)
u=g(x),则称函数
y
=
f
(
g
(
x
)
)
y=f(g(x))
y=f(g(x))为函数
y
=
f
(
u
)
y =f(u)
y=f(u)与
u
=
g
(
x
)
u =g(x)
u=g(x)的复合函数。其中y称为因变量,x称为自变量,u称为中间变量。
(2)求复合函数的定义域
①复合函数的定义域,是函数
y
=
f
[
g
(
x
)
]
y=f[g(x)]
y=f[g(x)]中x的取值范围;
②若函数
f
(
x
)
f(x)
f(x)的定义域为
(
a
,
b
)
(a,b)
(a,b),则复合函数
y
=
f
[
g
(
x
)
]
y=f[g(x)]
y=f[g(x)]的定义域由
a
<
g
(
x
)
<
b
a<g(x)<b
a<g(x)<b求出;
③若函数
y
=
f
[
g
(
x
)
]
y=f[g(x)]
y=f[g(x)]的定义域为
(
a
,
b
)
(a,b)
(a,b),则
f
(
x
)
f(x)
f(x)的定义域为
g
(
x
)
g(x)
g(x)在
a
<
x
<
b
a<x<b
a<x<b上的值域。
注意:
g
(
x
)
g(x)
g(x)的值域对应
y
=
f
(
u
)
y=f(u)
y=f(u)的定义域。对于复合函数,可以将内部的函数看成一个整体进行分析。此外,内部函数的值域对应外部函数的定义域。
(3)复合函数的单调性——【同增异减】
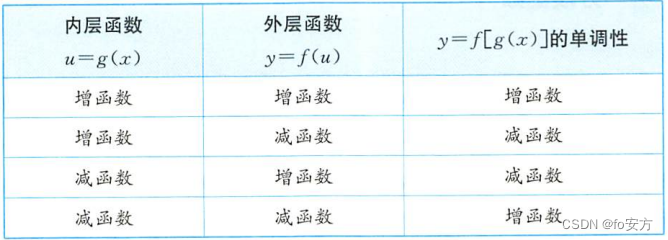
奇偶函数:
① 奇函数的性质
定义域关于原点对称,图像关于原点对称:
f
(
−
x
)
=
−
f
(
x
)
f(-x)=-f(x)
f(−x)=−f(x)
② 偶函数的性质
定义域关于原点对称,图像关于y轴对称:
f
(
−
x
)
=
f
(
x
)
f(-x)=f(x)
f(−x)=f(x)
反比例函数:
y
=
k
x
(
k
≠
0
)
y=\frac{k}{x}(k≠0)
y=xk(k=0)
在一个反比例函数图像上任取一点,过该点分别作x轴,y轴的平行线,与坐标轴围成的矩形面积为
∣
k
∣
|k|
∣k∣。