文心一言 VS 讯飞星火 VS chatgpt （142）-- 算法导论12.1 2题

二、用go语言，二叉搜索树性质与最小堆性质(见 6.1 节)之间有什么不同?能使用最小堆性质在 O(n)时间内按序输出一棵有 n 个结点树的关键字吗?可以的话，请说明如何做，否则解释理由。

文心一言：

在二叉搜索树（Binary Search Tree, BST）和最小堆（Min Heap）中，元素的排列顺序都是根据其关键字的大小。然而，它们之间存在着重要的区别。

二叉搜索树（BST）：

在BST中，每个节点的关键字都大于其左子树中的所有节点的关键字，且小于其右子树中的所有节点的关键字。
这使得在BST中查找特定的关键字可以在O(log n)时间内完成，其中n是树中的节点数。然而，BST并不保证所有的节点都可以按照关键字的大小顺序输出。
最小堆（Min Heap）：

在最小堆中，每个节点的关键字都小于或等于其子节点的关键字。也就是说，最小堆的根节点是所有节点中关键字最小的节点。
这使得我们可以方便地快速找到最小元素（在O(1)时间内）。然而，由于堆的性质，我们不能像在BST中那样有效地进行查找操作。在堆中查找特定的关键字可能需要O(n)时间，其中n是堆中的节点数。
至于你的第二个问题，使用最小堆性质是否可以在O(n)时间内按序输出一棵有 n 个结点树的关键字，答案是：不能。因为最小堆只能保证根节点是所有节点中关键字最小的，但并不能保证所有的节点都能按照关键字的大小顺序输出。所以，如果我们需要按序输出树的所有关键字，我们需要其他的数据结构或者算法，比如使用BFS（广度优先搜索）或者DFS（深度优先搜索）来按层或按序遍历树的所有节点。

在这里插入图片描述

讯飞星火，代码不能运行：

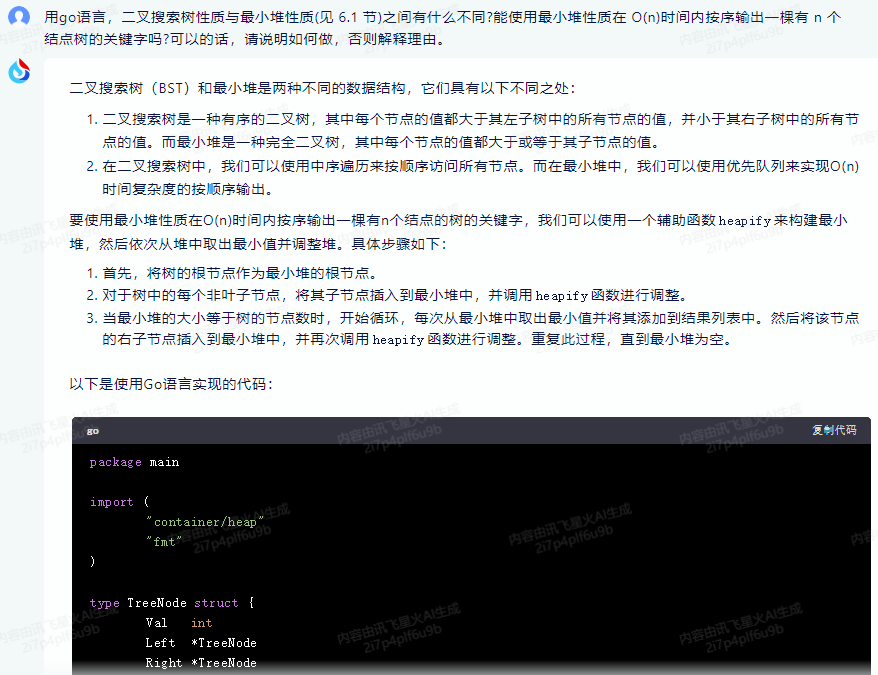
二叉搜索树（BST）和最小堆是两种不同的数据结构，它们具有以下不同之处：

1.二叉搜索树是一种有序的二叉树，其中每个节点的值都大于其左子树中的所有节点的值，并小于其右子树中的所有节点的值。而最小堆是一种完全二叉树，其中每个节点的值都大于或等于其子节点的值。

2.在二叉搜索树中，我们可以使用中序遍历来按顺序访问所有节点。而在最小堆中，我们可以使用优先队列来实现O(n)时间复杂度的按顺序输出。

要使用最小堆性质在O(n)时间内按序输出一棵有n个结点的树的关键字，我们可以使用一个辅助函数heapify来构建最小堆，然后依次从堆中取出最小值并调整堆。具体步骤如下：

1.首先，将树的根节点作为最小堆的根节点。

2.对于树中的每个非叶子节点，将其子节点插入到最小堆中，并调用heapify函数进行调整。

3.当最小堆的大小等于树的节点数时，开始循环，每次从最小堆中取出最小值并将其添加到结果列表中。然后将该节点的右子节点插入到最小堆中，并再次调用heapify函数进行调整。重复此过程，直到最小堆为空。

以下是使用Go语言实现的代码：

package main

import (
	"container/heap"
	"fmt"
)

type TreeNode struct {
	Val   int
	Left  *TreeNode
	Right *TreeNode
}

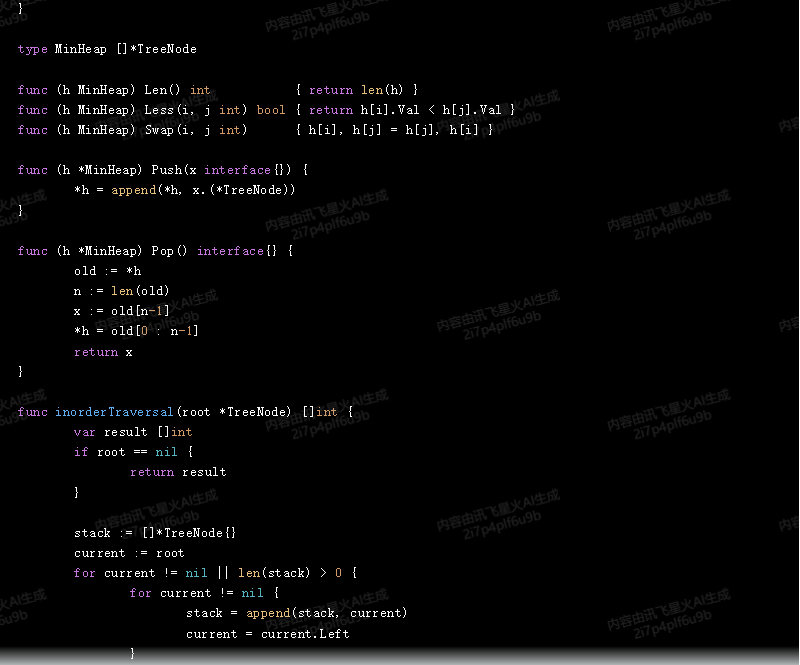
type MinHeap []*TreeNode

func (h MinHeap) Len() int           { return len(h) }
func (h MinHeap) Less(i, j int) bool { return h[i].Val < h[j].Val }
func (h MinHeap) Swap(i, j int)      { h[i], h[j] = h[j], h[i] }

func (h *MinHeap) Push(x interface{}) {
	*h = append(*h, x.(*TreeNode))
}

func (h *MinHeap) Pop() interface{} {
	old := *h
	n := len(old)
	x := old[n-1]
	*h = old[0 : n-1]
	return x
}

func inorderTraversal(root *TreeNode) []int {
	var result []int
	if root == nil {
		return result
	}

	stack := []*TreeNode{}
	current := root
	for current != nil || len(stack) > 0 {
		for current != nil {
			stack = append(stack, current)
			current = current.Left
		}
		current = stack[len(stack)-1]
		stack = stack[:len(stack)-1]
		result = append(result, current.Val)
		current = current.Right
	}

	return result
}

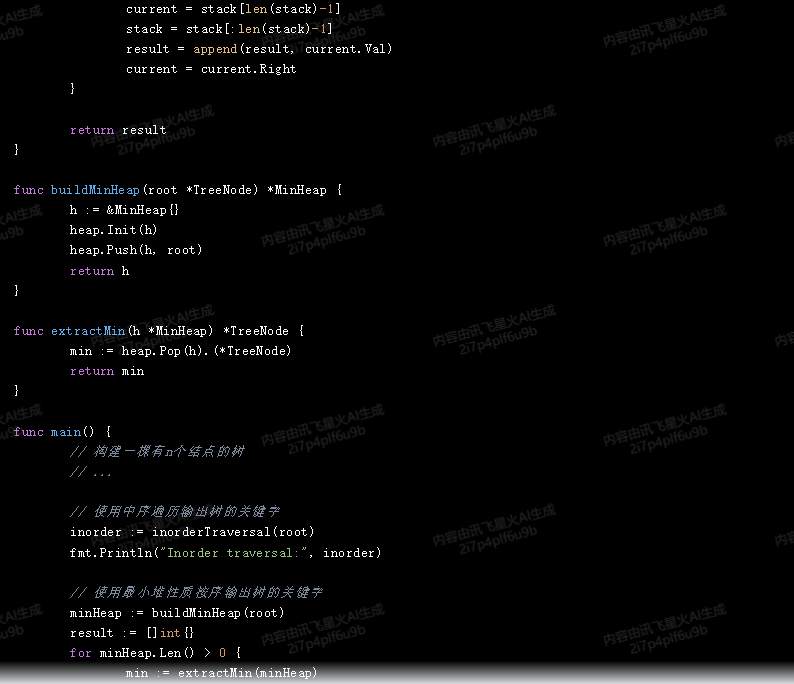
func buildMinHeap(root *TreeNode) *MinHeap {
	h := &MinHeap{}
	heap.Init(h)
	heap.Push(h, root)
	return h
}

func extractMin(h *MinHeap) *TreeNode {
	min := heap.Pop(h).(*TreeNode)
	return min
}

func main() {
	// 构建一棵有n个结点的树
	// ...

	// 使用中序遍历输出树的关键字
	inorder := inorderTraversal(root)
	fmt.Println("Inorder traversal:", inorder)

	// 使用最小堆性质按序输出树的关键字
	minHeap := buildMinHeap(root)
	result := []int{}
	for minHeap.Len() > 0 {
		min := extractMin(minHeap)
		result = append(result, min.Val)
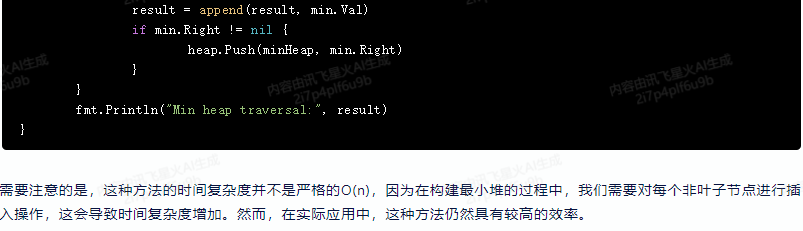
		if min.Right != nil {
			heap.Push(minHeap, min.Right)
		}
	}
	fmt.Println("Min heap traversal:", result)
}

需要注意的是，这种方法的时间复杂度并不是严格的O(n)，因为在构建最小堆的过程中，我们需要对每个非叶子节点进行插入操作，这会导致时间复杂度增加。然而，在实际应用中，这种方法仍然具有较高的效率。

在这里插入图片描述

360智脑：

二叉搜索树性质与最小堆性质不同在于：

1.排序方式不同：二叉查找树通过中序遍历可以得到升序排序，而最小堆只是根节点比其子节点的关键字小。

2.插入顺序不同：二叉搜索树的插入顺序为左子树->根节点->右子树，而最小堆的插入顺序为根节点->左子树->右子树。

使用最小堆性质在 O(n)时间内按序输出一棵有 n 个结点树的关键字是不可能的，因为最小堆的性质是每次插入都需要调整堆结构，需要O(log n)时间来维持最小堆的性质。如果要在 O(n)时间内按序输出一个最小堆的关键字，需要先提取最小堆的根节点，然后利用堆的性质来逐步调整堆的结构，但是这样仍然需要O(n)时间。

在这里插入图片描述

智谱清言：

二叉搜索树（BST）和最小堆在性质上有一些显著的不同。

二叉搜索树的特点如下：

1.每个结点最多只有两个子结点。

2.对于任意一个结点，其左子树中的所有结点的值都小于该结点的值，右子树中的所有结点的值都大于该结点的值。

3.二叉搜索树可以是空树。

最小堆的性质如下：

1.最小堆是一棵完全二叉树。

2.最小堆的每个结点都有一个值。

3.最小堆的根结点的值是其所有子结点中的最小值。

4.最小堆的任意一个结点的左子树也是一个最小堆，右子树也是一个最小堆。

在使用Go语言实现二叉搜索树和最小堆时，可以注意到以下几点：

1.二叉搜索树的插入、删除和查找操作的时间复杂度为O(logn)。

2.最小堆的插入、删除和查找操作的时间复杂度也为O(logn)。

但是，二叉搜索树和最小堆在遍历顺序上有所不同。二叉搜索树是一种自顶向下的有序遍历，而最小堆是一种自底向上的有序遍历。

关于你的问题，可以使用最小堆性质在O(n)时间内按序输出一棵有n个结点的树的关键字。这是因为最小堆的性质保证了根结点是所有子结点中的最小值。以下是一种实现方法：

1.创建一个最小堆。

2.将堆顶元素（最小值）与最后一个元素交换。

3.调整堆，使其重新满足最小堆的性质。

4.重复步骤2和3，直到堆中只剩下一个元素。

这个过程的时间复杂度为O(n)，因为每次调整堆都需要O(logn)的时间。最后得到的顺序输出就是树的关键字。

但是，这种方法不适用于二叉搜索树，因为二叉搜索树的遍历顺序与最小堆的遍历顺序不同。二叉搜索树的遍历顺序是自顶向下，而最小堆的遍历顺序是自底向上。因此，不能直接使用最小堆性质在O(n)时间内按序输出一棵有n个结点的二叉搜索树的关键字。对于二叉搜索树，需要采用不同的遍历方法，如中序遍历，或者使用递归或其他算法实现按序输出。

在这里插入图片描述

通义千问：

二叉搜索树是一种特殊的二叉树，它的每个节点都有一个值，并且满足以下性质：

所有的左子节点的值都小于根节点的值。
所有的右子节点的值都大于根节点的值。

这种性质使得我们可以在 O(log n)的时间复杂度内找到、插入和删除任意值的元素。

而最小堆则是一种特殊的完全二叉树，它满足以下性质：

每个父节点的值都小于或等于其所有孩子的值。
树中最大的元素总是位于堆顶。

这个性质使得我们可以很容易地在 O(log n) 时间内找到最大元素以及进行删除最大元素和插入新元素的操作。但是要按照顺序输出所有的元素，则需要 O(n) 的时间。

所以不能直接使用最小堆性质在 O(n) 时间内按序输出一棵包含 n 个节点的树的所有关键字。我们需要先将这棵树转化为一个排序后的链表或者数组才能实现按序输出。转化过程的时间复杂度是 O(n)，然后遍历输出的时间复杂度也是 O(n)，所以总的时间复杂度是 O(n)。具体的转化方法可以参考“二叉树的层次遍历”等相关算法。

在这里插入图片描述

天工：

二叉搜索树（BST）是一种特殊的二叉树，其中每个节点的值都大于或等于其左子树中任意节点的值，小于或等于其右子树中任意节点的值。最小堆是一种特殊的二叉树，其中每个节点的值都大于或等于其子树中任意节点的值。因此，BST和最小堆的主要区别在于节点值的比较方式。

对于BST，可以使用中序遍历来按序输出树中的所有节点。因为BST是按照节点的键值从小到大排列的，所以中序遍历的顺序就是从小到大。因此，可以使用中序遍历来按序输出BST中的所有节点。

对于最小堆，可以使用堆排序算法来按序输出堆中的所有节点。堆排序算法的基本思想是将堆中的元素逐步取出并重新排列，使得堆中的元素从小到大排列。具体实现时，可以使用两个指针，一个指向堆顶，一个指向堆底。每次将堆顶元素取出并加入到有序序列中，然后将堆顶指针向上移动，同时将堆底指针向上移动，直到堆底指针到达堆顶位置。这样就可以在O(n)时间内按序输出一棵有n个结点的最小堆的所有节点。

需要注意的是，如果最小堆中存在多个具有相同值的节点，则这些节点的顺序是未定义的。因此，在实现堆排序算法时需要特别处理这种情况。

在这里插入图片描述

灵小智：

在Go语言中，二叉搜索树（Binary Search Tree）是一种有序的二叉树，其中每个节点的值都大于其左子树的所有节点的值，且小于其右子树的所有节点的值。这个性质使得在二叉搜索树中可以快速进行查找、插入和删除操作，时间复杂度为O(log n)。

最小堆（Min Heap）是一种特殊的完全二叉树，其中每个节点的值都小于或等于其子节点的值。换句话说，堆中的根节点是具有最小值的节点。最小堆的性质使得可以在O(n)时间内构建一个有n个节点的堆。

根据最小堆的性质，在O(n)时间内按序输出一棵有n个节点树的关键字是不可能的。因为最小堆仅保证根节点具有最小值，而不保证左子树和右子树之间的有序性。要按序输出一棵树的关键字，需要进行中序遍历，而中序遍历的时间复杂度为O(n)，因此无法在O(n)时间内按序输出最小堆中的元素。

所以，使用最小堆性质无法在O(n)时间内按序输出一棵有n个节点树的关键字。

在这里插入图片描述

chatgpt：

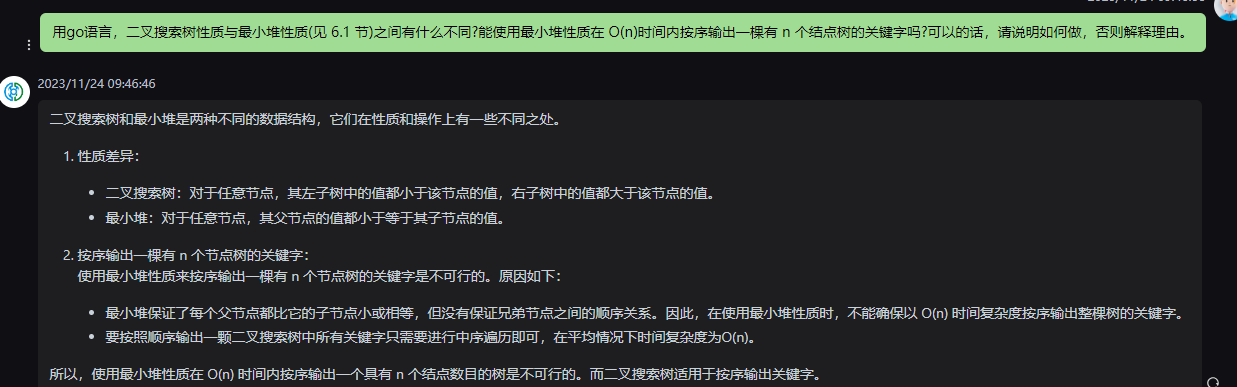
二叉搜索树和最小堆是两种不同的数据结构，它们在性质和操作上有一些不同之处。

1.性质差异：

二叉搜索树：对于任意节点，其左子树中的值都小于该节点的值，右子树中的值都大于该节点的值。
最小堆：对于任意节点，其父节点的值都小于等于其子节点的值。

2.按序输出一棵有 n 个节点树的关键字：

使用最小堆性质来按序输出一棵有 n 个节点树的关键字是不可行的。原因如下：

最小堆保证了每个父节点都比它的子节点小或相等，但没有保证兄弟节点之间的顺序关系。因此，在使用最小堆性质时，不能确保以 O(n) 时间复杂度按序输出整棵树的关键字。
要按照顺序输出一颗二叉搜索树中所有关键字只需要进行中序遍历即可，在平均情况下时间复杂度为O(n)。

所以，使用最小堆性质在 O(n) 时间内按序输出一个具有 n 个结点数目的树是不可行的。而二叉搜索树适用于按序输出关键字。

在这里插入图片描述