【数据结构】二叉树概念 | 满二叉树

【数据结构】二叉树概念 | 满二叉树 | 完全二叉树

news2024/9/24 18:52:59

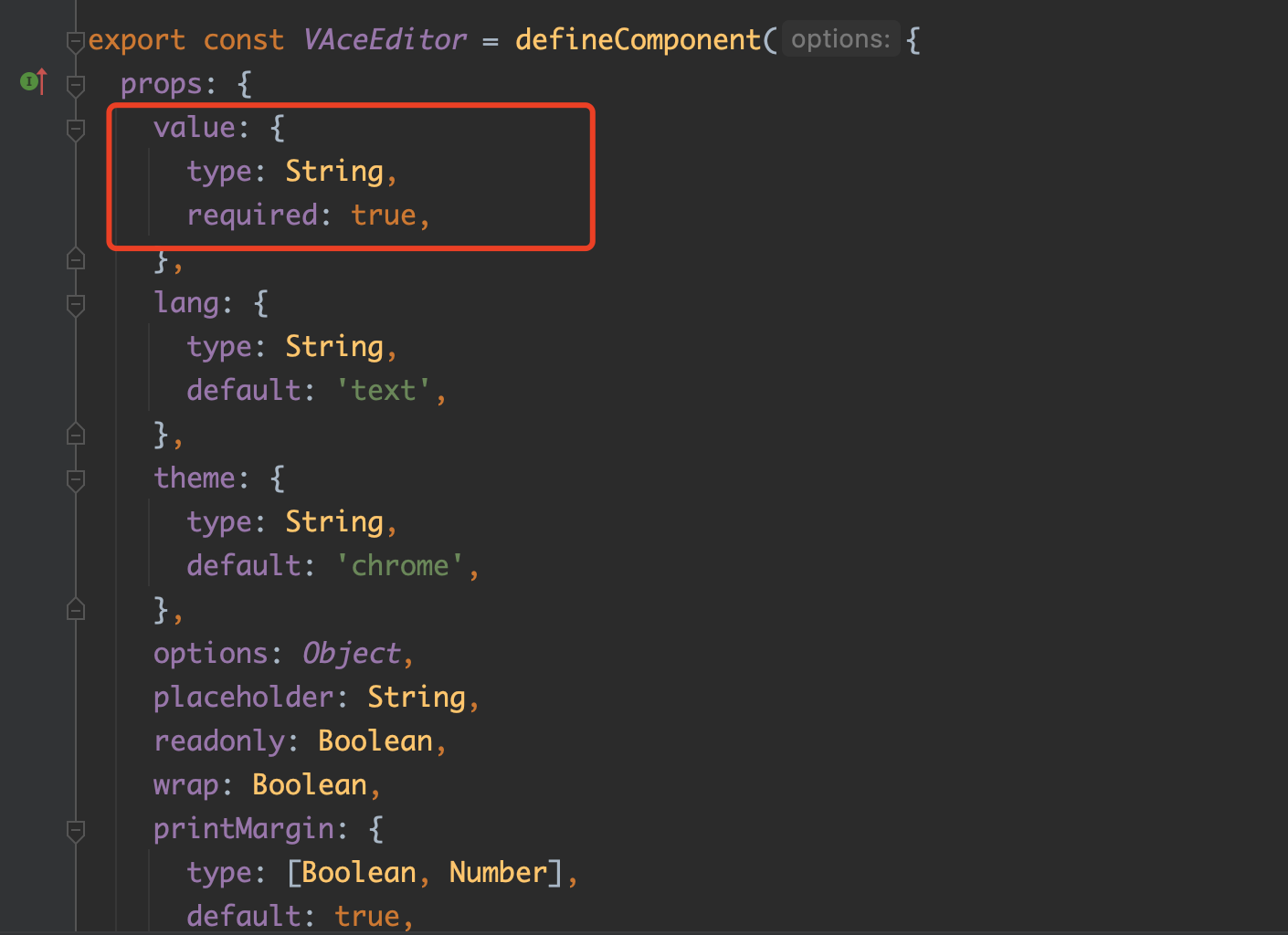
二叉树的概念

二叉树在实践中用的很多。

一棵二叉树是结点的一个有限集合，该集合：

或者为空；
由一个根结点加上两棵别称为左子树和右子树的二叉树组成。
二叉树最多两个孩子。

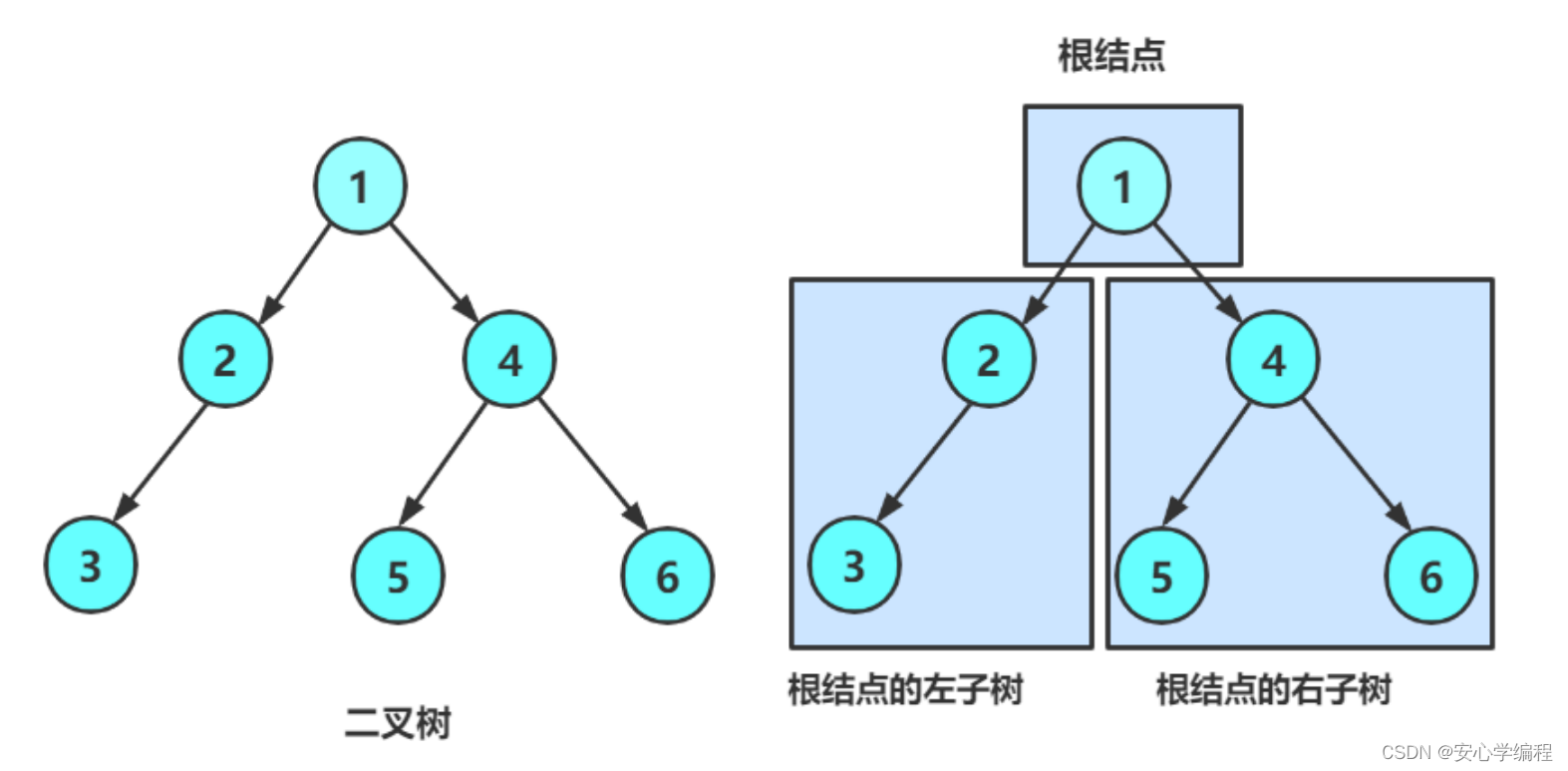
这里注意：二叉树并不是度为2的树。

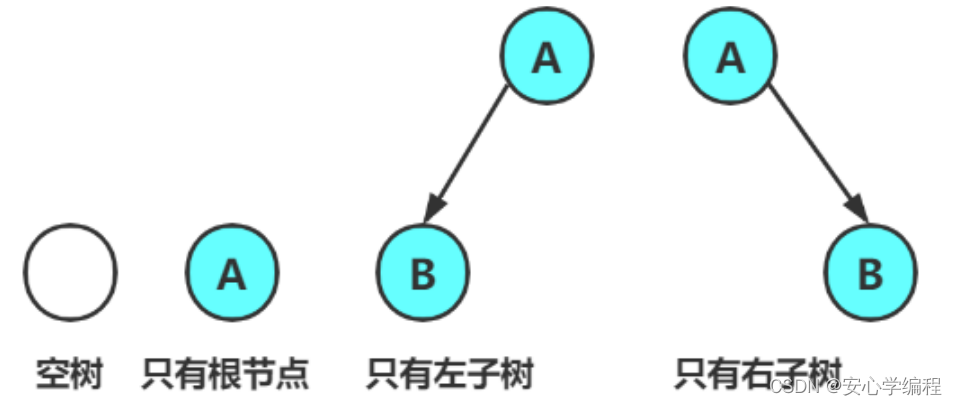
二叉树的度最大值是2，并不是说它的度一定为2。所以一下这四种情况也均是二叉树：

空树
只有根节点
只有左子树
只有右子树
左右子树均存在

二叉树不存在度大于2的节点；

二叉树的子树有左右之分，次序是不能颠倒的，因此二叉树是有序树。

二叉树通俗也可以理解为对树进行了“计划生育”。 “计划生育”也就是生两个小孩，但是是每一家来说都是生两个吗？

那么度为2的一定是二叉树吗？

度为2一定是二叉树。度为2的话，那么所有节点的最大的度就是2，而二叉树的概念是不存在度大于2的节点。
二叉树是一个特殊的树，它的度最大为2，但是并没有说一定为2。

特殊的二叉树

满二叉树

一个二叉树，如果每一个层的结点数都达到最大值，那么这个二叉树就是满二叉树。也就是说，如果一个二叉树的成熟为K，那么结点总数就是 $2^{K}-1$ ，那么它就是满二叉树。

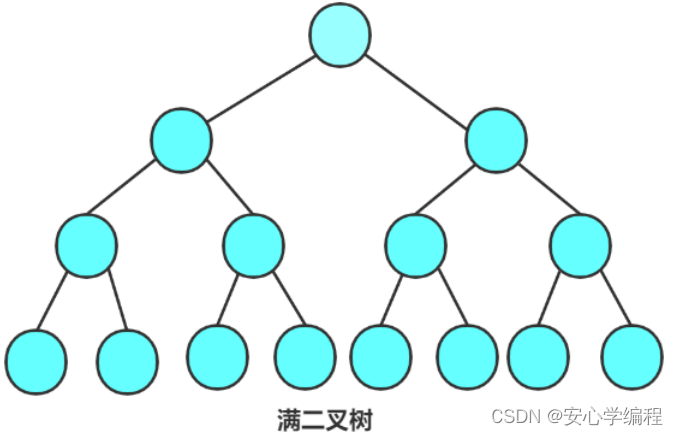
根据上图：

假设高度为h，那么就会有 $2^{h}-1$ 的节点；
那么假设树有N个节点的话，那就是 $2^{h}-1=N$ ；那么高度就为 $h=\log _{2}(N+1)$ 。

完全二叉树

完全二叉树，前h-1层都是满的，最后一层不一定满，但是从左到右必须连续。

完全二叉树是效率很高的数据结构，完全二叉树是由满二叉树而引出来的。对于深入为K的，有n个节点的二叉树，当且仅当其每一个节点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。要注意的是满二叉树是一种特殊的完全二叉树。

这里注意二叉树顺序是固定的，必须是连续的。

假设完全二叉树的高度为h，那么它的结点数量是多少呢？

完全二叉树的最后一层的范围： $\left [ 2^{h-1},2^{h}-1 \right ]$

思路：

这里我们想在满二叉树中，结点数为 $2^{h}-1$ ；
那么满二叉树中的上一层就是有 $2^{h-1}-1$ ；
因为完全二叉树就是满二叉树的基础上，最后一层不满，也就是最后一层的结点数最多有 $2^{h-1}$ ，最少有1个；
所以根据等比公式可以求得出完全二叉树最后一层的范围为： $\left [ 2^{h-1} , 2^{h}-1 \right ]$ 。