朴素贝叶斯 概述
贝叶斯分类是一类分类算法的总称,这类算法均以贝叶斯定理为基础,故统称为贝叶斯分类。本章首先介绍贝叶斯分类算法的基础——贝叶斯定理。最后,我们通过实例来讨论贝叶斯分类的中最简单的一种: 朴素贝叶斯分类。
贝叶斯理论 & 条件概率
贝叶斯理论
我们现在有一个数据集,它由两类数据组成,数据分布如下图所示:
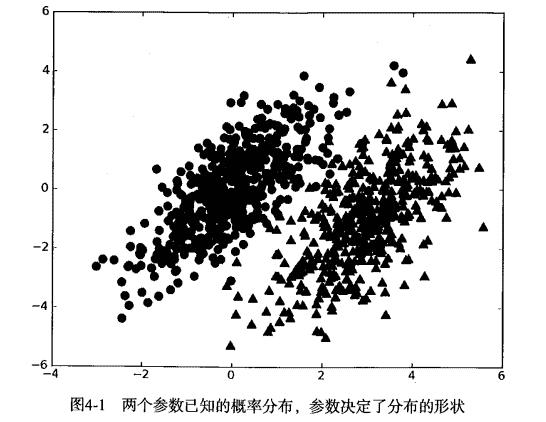
我们现在用 p1(x,y) 表示数据点 (x,y) 属于类别 1(图中用圆点表示的类别)的概率,用 p2(x,y) 表示数据点 (x,y) 属于类别 2(图中三角形表示的类别)的概率,那么对于一个新数据点 (x,y),可以用下面的规则来判断它的类别:
- 如果 p1(x,y) > p2(x,y) ,那么类别为1
- 如果 p2(x,y) > p1(x,y) ,那么类别为2
也就是说,我们会选择高概率对应的类别。这就是贝叶斯决策理论的核心思想,即选择具有最高概率的决策。
条件概率
如果你对 p(x,y|c1)