5.1 PBR基础 BRDF介绍

基于物理的渲染（Physically Based Rendering，PBR）是指使用基于物理原理和微平面理论建模的着色/光照模型，以及使用从现实中测量的表面参数来准确表示真实世界材质的渲染理念。

一、反射率方程

理论基础放在参考链接里。

直接开始分析公式里各项含义。

二、BRDF项

1. F(i,h）：菲涅尔方程（Fresnel Equation）

描述不同的表面角下表面所反射的光线所占的比率。

对于菲涅尔（Fresnel）项，业界方案一般都采用Schlick的Fresnel近似，因为计算成本低廉，而且精度足够：

菲涅尔项的常见模型可以总结如下：

Cook-Torrance [1982]
Schlick [1994]
Gotanta [2014]

2. G(i,o,h）：几何函数（Geometry Function）

描述微平面自成阴影的属性，即m = h的未被遮蔽的表面点的百分比。

目前较为常用的是其中最为简单的形式，分离遮蔽阴影（Separable Masking and Shadowing Function）。

该形式将几何项G分为两个独立的部分：光线方向（light）和视线方向（view），并对两者用相同的分布函数来描述。根据这种思想，结合法线分布函数（NDF）与Smith几何阴影函数，于是有了以下新的Smith几何项：

Smith-GGX
Smith-Beckmann
Smith-Schlick
Schlick-Beckmann
Schlick-GGX

其中UE4的方案是上面列举中的“Schlick-GGX”，即基于Schlick近似，将k映射为

,去匹配GGX Smith方程：

3. D(h)：法线分布函数（Normal Distribution Function）

描述微面元法线分布的概率，即正确朝向的法线的浓度。即具有正确朝向，能够将来自l的光反射到v的表面点的相对于表面面积的浓度。

法线分布函数（Normal Distribution Function, NDF）D的常见模型可以总结如下：

Beckmann[1963]
Blinn-Phong[1977]
GGX [2007] / Trowbridge-Reitz[1975]
Generalized-Trowbridge-Reitz(GTR) [2012]
Anisotropic Beckmann[2012]
Anisotropic GGX [2015]

其中，业界较为主流的法线分布函数是GGX（Trowbridge-Reitz），因为具有更好的高光长尾：

4.分母 4(n·l)(n·v）：校正因子（correctionfactor）

作为微观几何的局部空间和整个宏观表面的局部空间之间变换的微平面量的校正。

三、Disney Principled BRDF的着色模型

核心BRDF 模型

核心BRDF模型方面，Disney采用了通用的microfacet Cook-Torrance BRDF着色模型：

漫反射项（Diffuse）：Disney Diffuse

Disney使用了Schlick Fresnel近似，并修改掠射逆反射（grazing retroreflection response）以达到其特定值由粗糙度值确定，而不是简单为0。

Disney Diffuse漫反射模型的公式为：

其中，

以下为上述Disney Diffuse的Shader实现代码：

// [Burley 2012, "Physically-Based Shading at Disney"]
float3 Diffuse_Burley_Disney( float3 DiffuseColor, float Roughness, float NoV, float NoL, float VoH )
{
	float FD90 = 0.5 + 2 * VoH * VoH * Roughness;
	float FdV = 1 + (FD90 - 1) * Pow5( 1 - NoV );
	float FdL = 1 + (FD90 - 1) * Pow5( 1 - NoL );
	return DiffuseColor * ( (1 / PI) * FdV * FdL );
}

菲涅尔项（Specular F）：Schlick Fresnel

菲涅尔项（Specular F）方面，Disney表示Schlick Fresnel近似已经足够精确，且比完整的菲涅尔方程简单得多; 而由于其他因素，Schlick Fresne近似引入的误差明显小于其他因素产生的误差。Schlick Fresnel 近似公式如下：

其中：

常数F0表示垂直入射时的镜面反射率。
θd为半矢量h和视线矢量v之间的夹角

以下为Schlick Fresnel的Shader实现代码：

// [Schlick 1994, "An Inexpensive BRDF Model for Physically-Based Rendering"]
float3 F_Schlick(float HdotV, float3 F0)
{
    return F0 + (1 - F0) * pow(1 - HdotV , 5.0);
}

另外，Disney在SIGGRAPH 2015上对此项进行了修订，提出在介质间相对IOR接近1时，Schlick近似误差较大，这时可以直接用精确的菲涅尔方程：

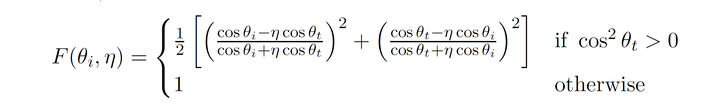
几何项（Specular G）：Smith-GGX

几何项（Specular G）方面，对于主镜面波瓣（primary specular lobe），Disney参考了 Walter的近似方法，使用Smith GGX导出的G项，并将粗糙度参数进行重映射以减少光泽表面的极端增益，即将α 从[0, 1]重映射到[0.5, 1]，α的值为(0.5 + roughness/2)^2。从而使几何项的粗糙度变化更加平滑，更便于美术人员的使用。

以下为Smith GGX的几何项的表达式：

另外，对于对清漆层进行处理的次级波瓣（secondary lobe），Disney没有使用Smith G推导，而是直接使用固定粗糙度为0.25的GGX的 G项，便可以得到合理且很好的视觉效果。

几何项的Shader实现代码如下：

/法线分布项（Specular D）：GTR

可以发现，上式中：
● γ=1时，GTR即Berry分布
● γ=2时，GTR即Trowbridge-Reitz分布
以下为各种γ值的GTR分布曲线与θh的关系图示：
另外，Disney Principled BRDF中使用了两个固定的镜面反射波瓣（specular lobe），且都使用GTR模型，可以总结如下：
● 主波瓣（primary lobe）
  ○ 使用γ= 2的GTR（即GGX分布）
  ○ 代表基础底层材质（Base Material）的反射
  ○ 可为各项异性（anisotropic） 或各项同性（isotropic）的金属或非金属
● 次级波瓣（secondary lobe）
  ○ 使用γ= 1的GTR（即Berry分布）
  ○ 代表基础材质上的清漆层（ClearCoat Layer）的反射
  ○ 一般为各项同性（isotropic）的非金属材质，即清漆层（ClearCoat Layer）
以下是γ= 1和γ= 2时GTR分布的Shader实现代码：
// Generalized-Trowbridge-Reitz distribution
float D_GTR1(float alpha, float dotNH)
{
    float a2 = alpha * alpha;
    float cos2th = dotNH * dotNH;
    float den = (1.0 + (a2 - 1.0) * cos2th);

    return (a2 - 1.0) / (PI * log(a2) * den);
}

float D_GTR2(float alpha, float dotNH)
{
    float a2 = alpha * alpha;
    float cos2th = dotNH * dotNH;
    float den = (1.0 + (a2 - 1.0) * cos2th);

    return a2 / (PI * den * den);
}
以及各项异性的版本：
float D_GTR2_aniso(float dotHX, float dotHY, float dotNH, float ax, float ay)
{
    float deno = dotHX * dotHX / (ax * ax) + dotHY * dotHY / (ay * ay) + dotNH * dotNH;
    return 1.0 / (PI * ax * ay * deno * deno);
}/ Geometric Shadowing function 
float G_SchlickSmithGGX(float NdotL, float NdotV, float roughness)
{
    float r = (roughness + 1.0);
    float k = (r*r) / 8.0;
    float GL = NdotL / (NdotL * (1.0 - k) + k);
    float GV = NdotV / (NdotV * (1.0 - k) + k);
    return GL * GV;
}

// Smith GGX G项，各项同性版本
float smithG_GGX(float NdotV, float alphaG)
{
    float a = alphaG * alphaG;
    float b = NdotV * NdotV;
    return 1 / (NdotV + sqrt(a + b - a * b));
}

// Smith GGX G项，各项异性版本
// Derived G function for GGX
float smithG_GGX_aniso(float dotVN, float dotVX, float dotVY, float ax, float ay)
{
	return 1.0 / (dotVN + sqrt(pow(dotVX * ax, 2.0) + pow(dotVY * ay, 2.0) + pow(dotVN, 2.0)));
}

法线分布项（Specular D）：GTR

可以发现，上式中：

γ=1时，GTR即Berry分布
γ=2时，GTR即Trowbridge-Reitz分布

以下为各种γ值的GTR分布曲线与θh的关系图示：

另外，Disney Principled BRDF中使用了两个固定的镜面反射波瓣（specular lobe），且都使用GTR模型，可以总结如下：

主波瓣（primary lobe）

- 使用γ= 2的GTR（即GGX分布）
- 代表基础底层材质（Base Material）的反射
- 可为各项异性（anisotropic）或各项同性（isotropic）的金属或非金属

次级波瓣（secondary lobe）

- 使用γ= 1的GTR（即Berry分布）
- 代表基础材质上的清漆层（ClearCoat Layer）的反射
- 一般为各项同性（isotropic）的非金属材质，即清漆层（ClearCoat Layer）

以下是γ= 1和γ= 2时GTR分布的Shader实现代码：

// Generalized-Trowbridge-Reitz distribution
float D_GTR1(float alpha, float dotNH)
{
    float a2 = alpha * alpha;
    float cos2th = dotNH * dotNH;
    float den = (1.0 + (a2 - 1.0) * cos2th);

    return (a2 - 1.0) / (PI * log(a2) * den);
}

float D_GTR2(float alpha, float dotNH)
{
    float a2 = alpha * alpha;
    float cos2th = dotNH * dotNH;
    float den = (1.0 + (a2 - 1.0) * cos2th);

    return a2 / (PI * den * den);
}

以及各项异性的版本：

float D_GTR2_aniso(float dotHX, float dotHY, float dotNH, float ax, float ay)
{
    float deno = dotHX * dotHX / (ax * ax) + dotHY * dotHY / (ay * ay) + dotNH * dotNH;
    return 1.0 / (PI * ax * ay * deno * deno);
}