【算法】经典算法题

news2024/9/27 5:56:59

文章目录

  • 专题一：双指针
    • 1. 移动零
    • 2. 复写零
    • 3. 快乐数
    • 4. 盛最多水的容器
    • 5. 有效三角形的个数
    • 6. 查找总价格为目标值的两个商品
    • 7. 三数之和
    • 8. 四数之和
  • 专题二：滑动窗口
    • 1. 长度最小的子数组
    • 2. 无重复字符的最长字串
    • 3. 最大连续1的个数 III
    • 4. 将 x 减到 0 的最小操作数

专题一：双指针

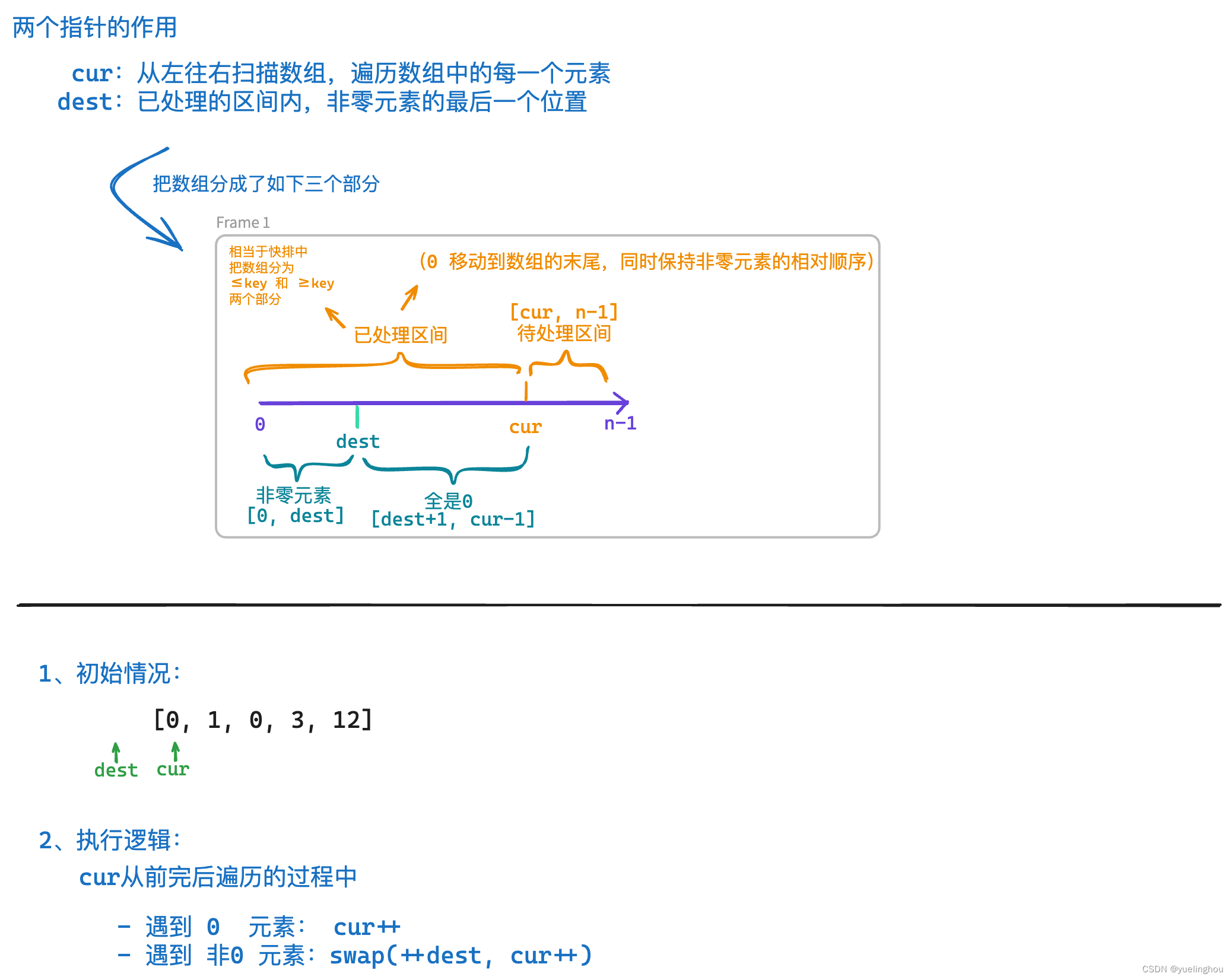
1. 移动零

在这里插入图片描述

题目解析
在这里插入图片描述

算法原理
在这里插入图片描述

代码编写

// 写法一
class Solution 
{
public:
    void moveZeroes(vector<int>& nums) 
    {
        // 1、下标初始化
        int dest = -1, cur = 0;
        // 2、数组划分
        while(cur < nums.size())
        {
            if(nums[cur]) 
                swap(nums[++dest], nums[cur++]);
            else 
                ++cur;
        }
    }
};

// 写法二
class Solution 
{
public:
    void moveZeroes(vector<int>& nums) 
    {
       for(int dest = -1, cur = 0; cur < nums.size(); ++cur)
            if(nums[cur]) // 处理 非0 元素
                swap(nums[++dest], nums[cur]);
    }
};

/*
- 时间复杂度：O(n)
- 空间复杂度：O(1)
*/

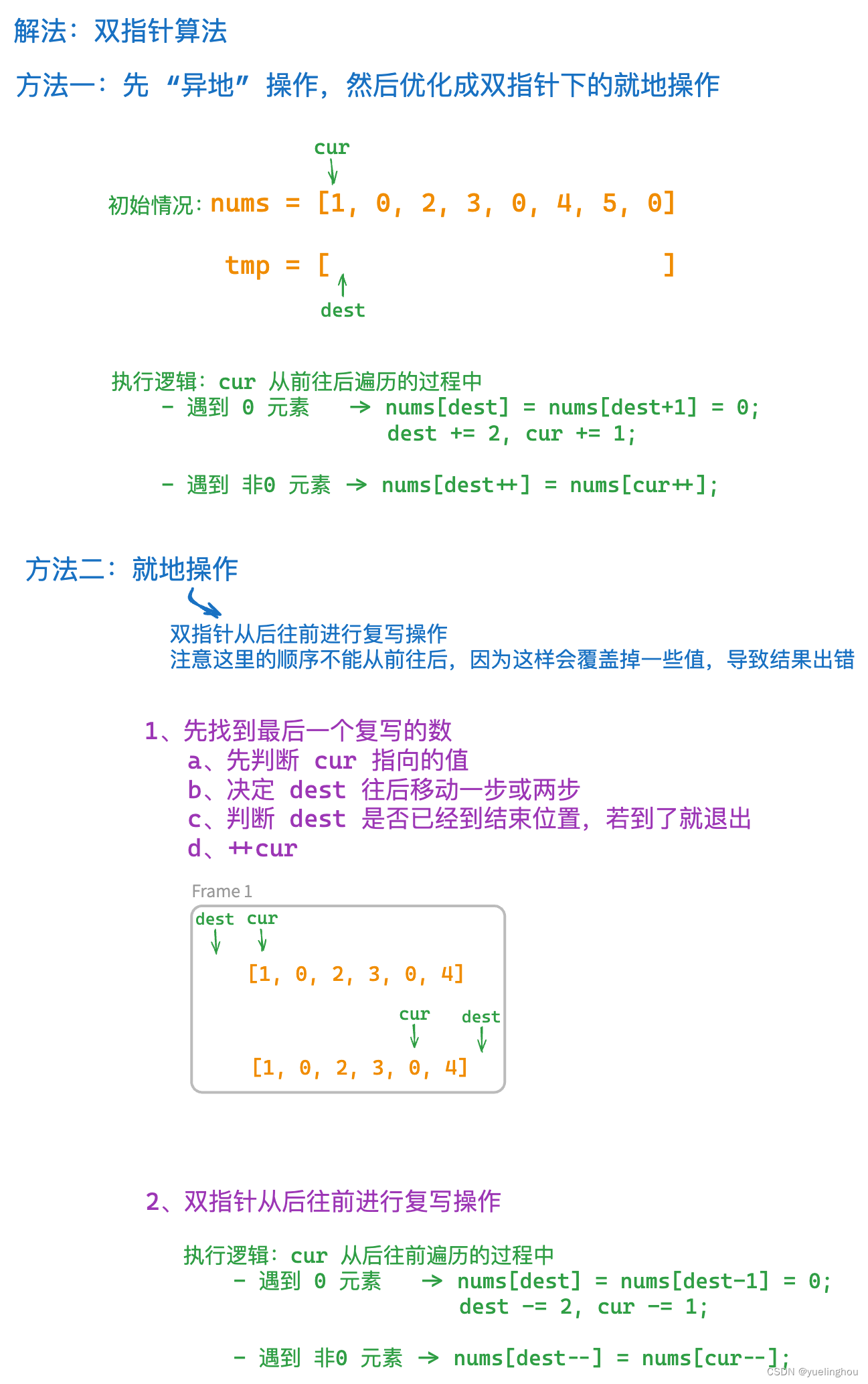
2. 复写零

在这里插入图片描述

算法原理
在这里插入图片描述

代码编写

class Solution 
{
public:
    void duplicateZeros(vector<int>& nums) 
    {
        // 1、初始化
        int dest = -1, cur = 0, n = nums.size();
        // 2、找到最后一个复写的数
        while(true)
        {
            if(nums[cur]) dest += 1;
            else dest += 2;
            if(dest >= n - 1) break;
            ++cur;
        }
        cout << nums[cur] << endl;
        // 1.5、预处理 -> 让 dest 的下标有效
        if(dest == n)
        {
            if(nums[cur]) --cur, --dest;
            else 
            {
                nums[n - 1] = 0;
                dest -= 2;
                cur -= 1;
            }
        }
        // 2、双指针从后往前进行复写操作
        while(cur >= 0)
        {
            if(nums[cur]) nums[dest--] = nums[cur--];
            else
            {
                nums[dest--] = 0;
                nums[dest--] = 0;
                cur--;
            } 
        }
    }
};
/*
- 时间复杂度：O(n)
- 空间复杂度：O(1)
*/

3. 快乐数

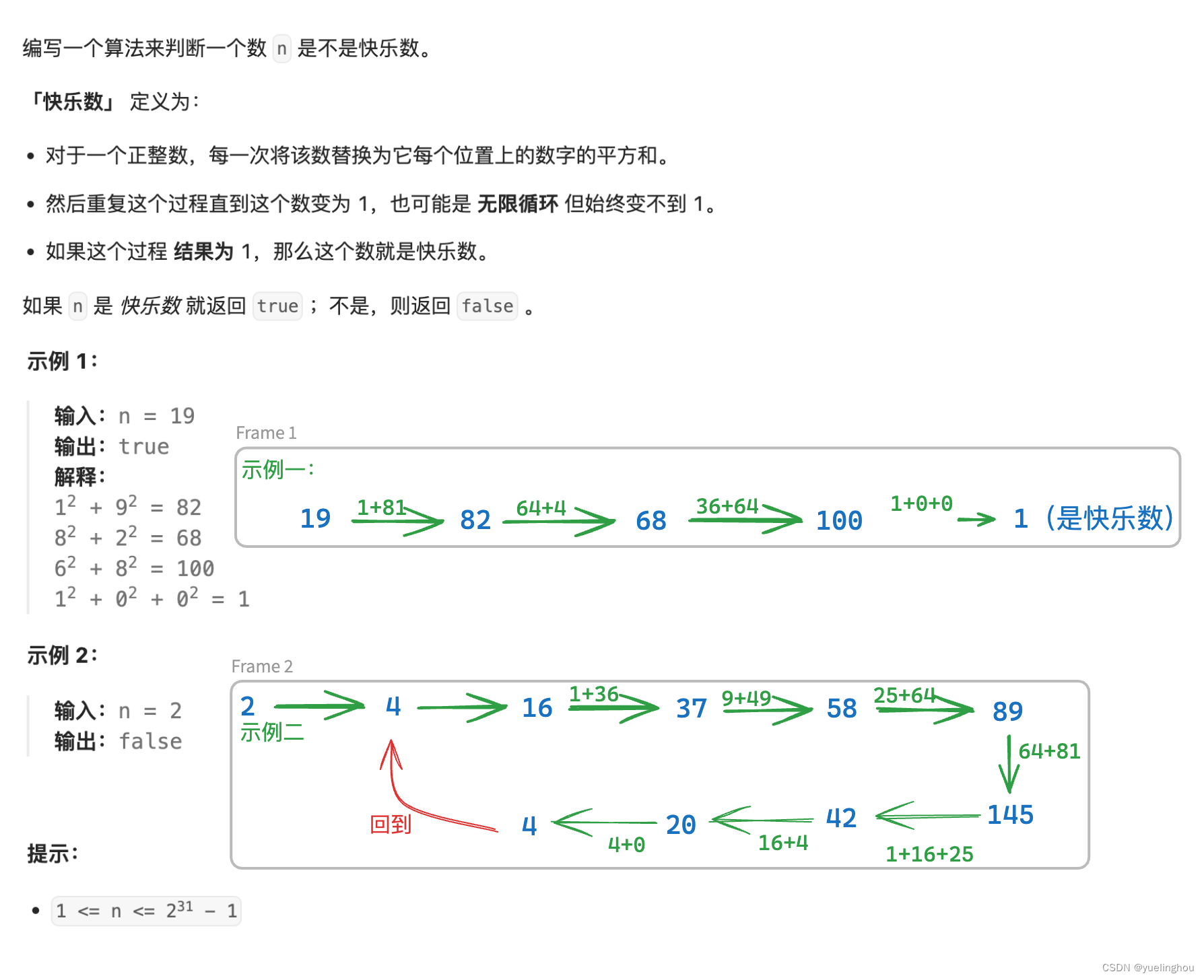
在这里插入图片描述

算法原理
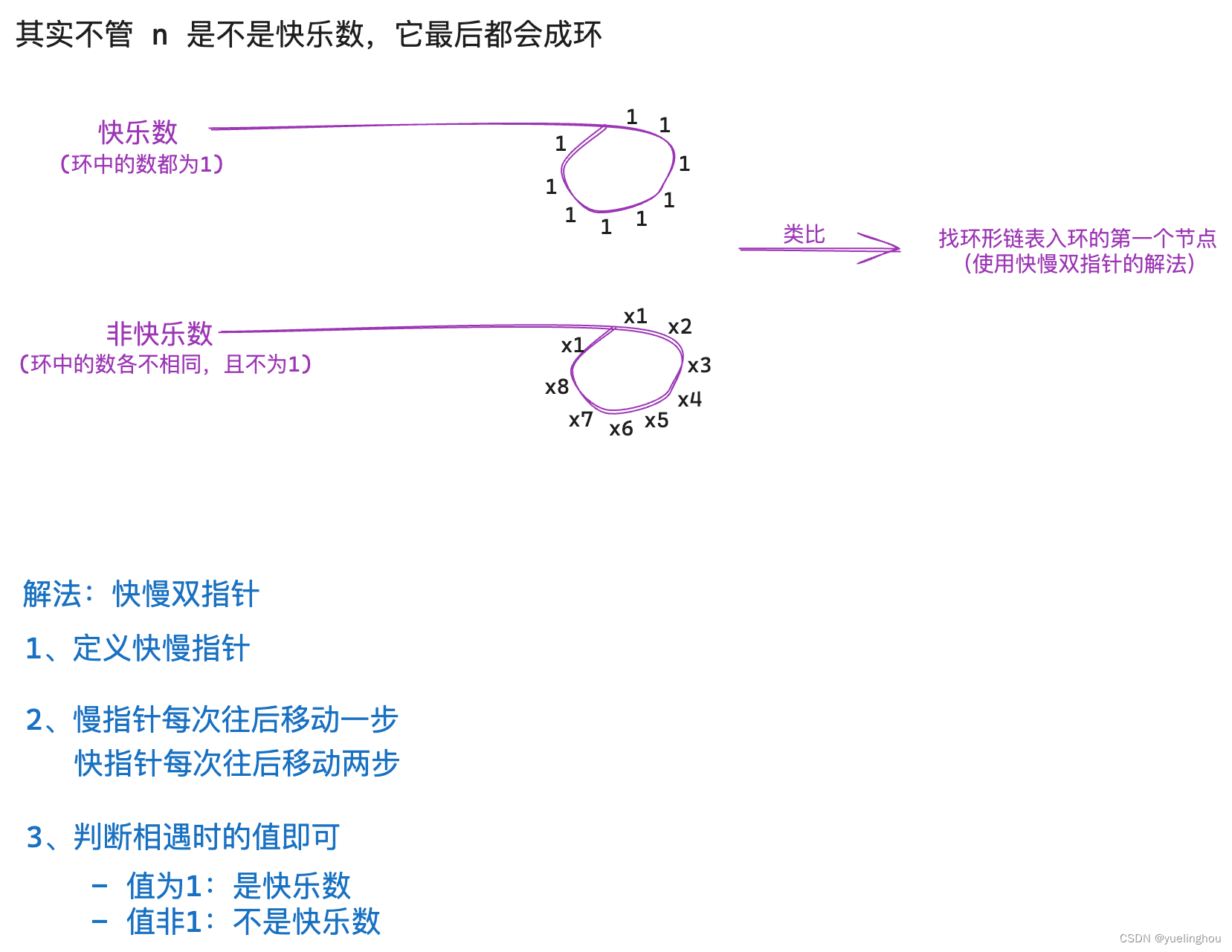
在这里插入图片描述

代码编写

class Solution 
{
private:
    // 计算每个位置上的数字的平方和
    inline static int BitSum(int num)
    {
        int ret = 0;
        while(num)
        {
            int t = num % 10;
            ret += t * t;
            num /= 10;
        }
        return ret;
    }

public:
    bool isHappy(int n) 
    {
        int slow = n, fast = BitSum(n);
        while(slow != fast)
        {
            slow = BitSum(slow);
            fast = BitSum(BitSum(fast));
        }
        return slow == 1;
    }
};

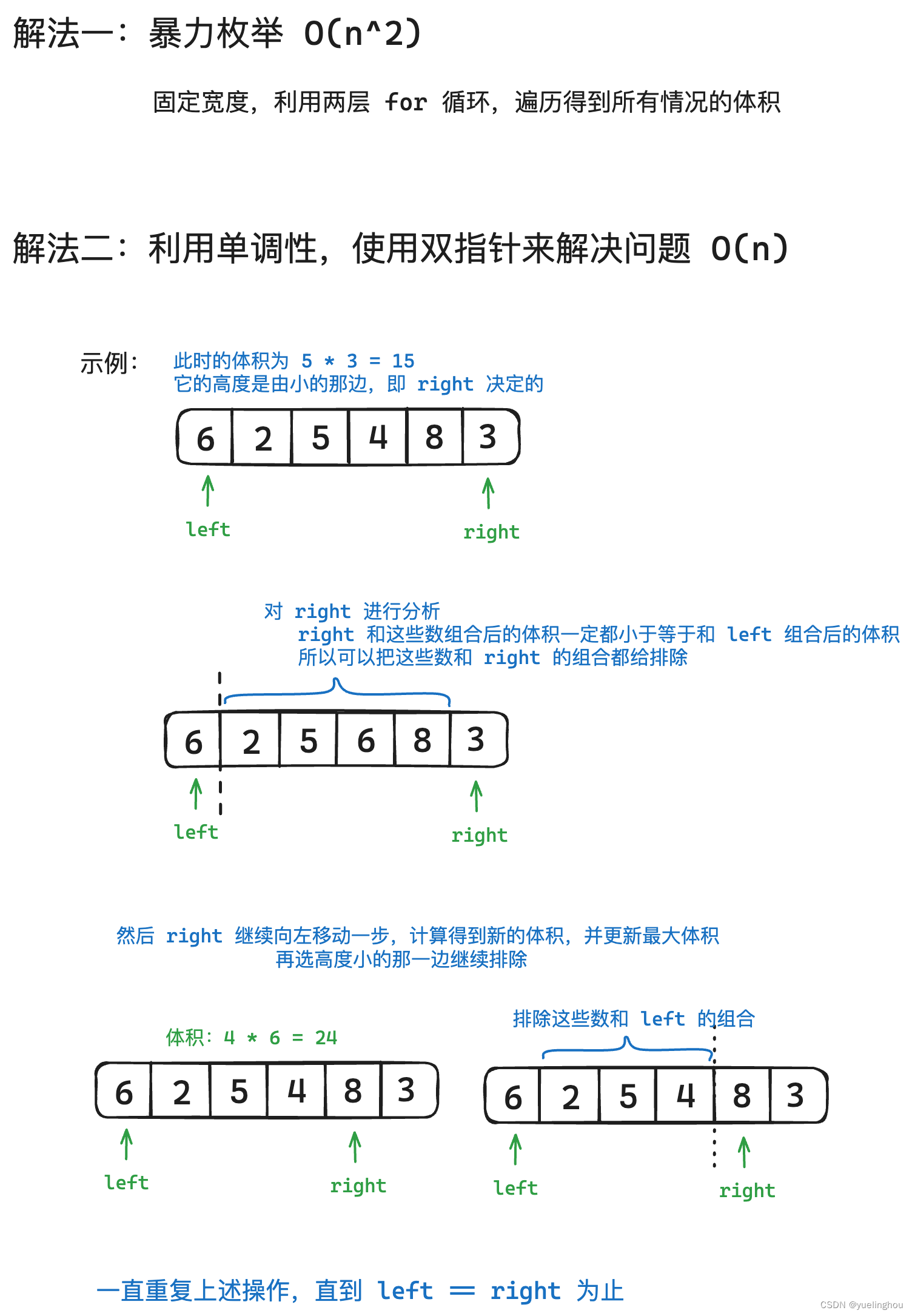
4. 盛最多水的容器

在这里插入图片描述

算法原理
在这里插入图片描述

代码编写

class Solution 
{
public:
    int maxArea(vector<int>& height) 
    {
        int left = 0, right = height.size() - 1;
        int ret = INT_MIN;
        while(left != right)
        {
            // 容积 = 长度 * 高度
            int v = (right - left) * min(height[left], height[right]);
            ret = max(ret, v);
            // 移动指针 - 谁小移动谁
            height[left] < height[right] ? ++left : --right;
        }
        return ret;
    }
};
/*
- 时间复杂度：O(n)
- 空间复杂度：O(1)
*/

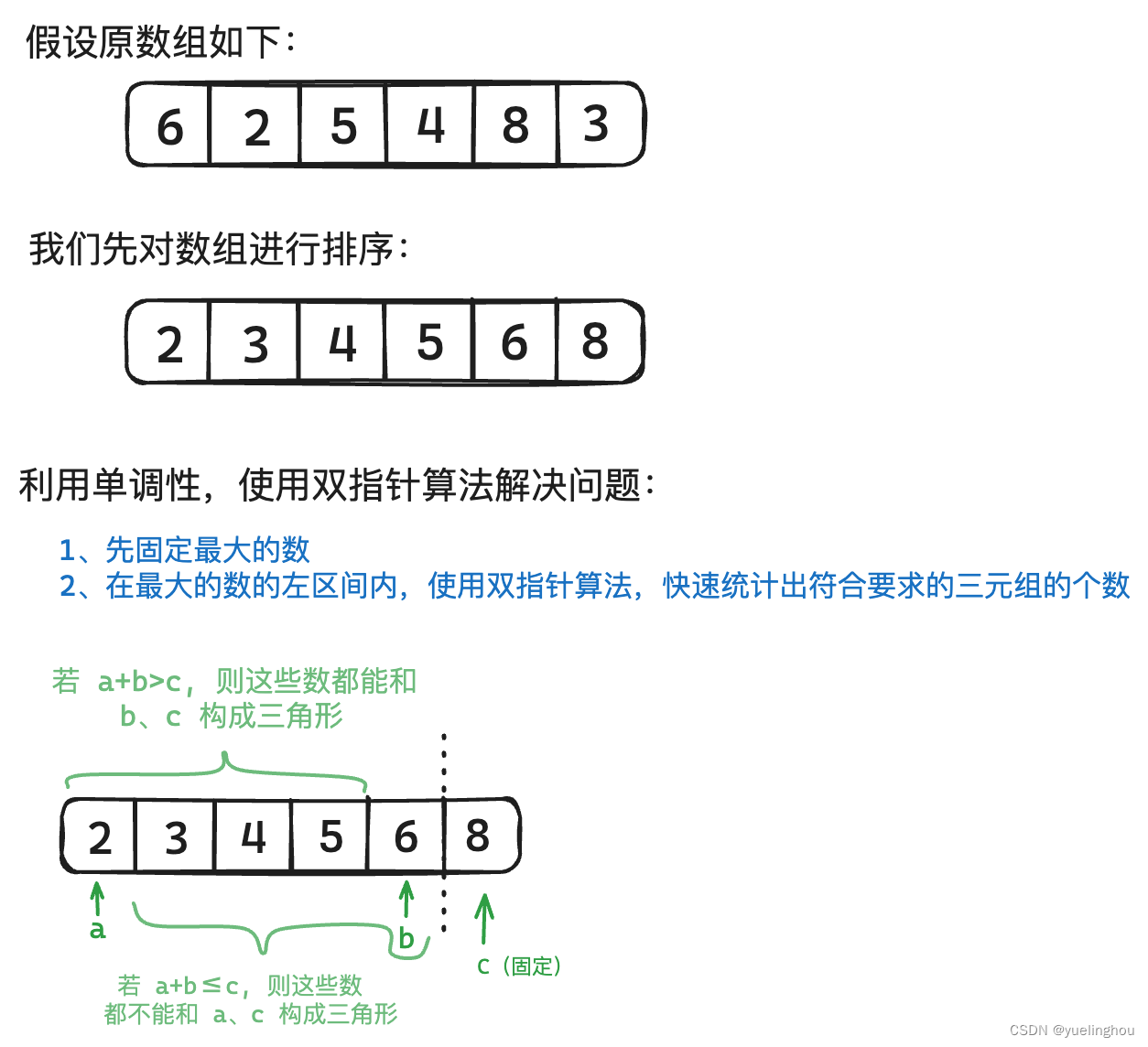
5. 有效三角形的个数

在这里插入图片描述

算法原理
在这里插入图片描述

代码编写

class Solution 
{
public:
    int triangleNumber(vector<int>& nums) 
    {
        // 1、优化
        sort(nums.begin(), nums.end());
        // 2、利用双指针解决问题
        int ret = 0, n = nums.size();
        for(int i = n - 1; i >= 2; --i)
        {
            int left = 0, right = i - 1;
            while(left < right)
            {
                // 当 a+b>c ，a下标属于 [left, right-1]时，都能和 b、c 构成三角形
                // 当 a+b<=c ，b下标属于[left-1, right]时，都不能和 a、c 构成三角形
                if(nums[left] + nums[right] > nums[i])
                {
                    ret += right - left;
                    --right;
                }
                else ++left;
            }
        }
        // 返回值
        return ret;
    }
};

/*
- 时间复杂度：O(n^2)
- 空间复杂度：O(1)
*/

6. 查找总价格为目标值的两个商品

在这里插入图片描述

算法原理
在这里插入图片描述

代码编写

class Solution 
{
public:
    vector<int> twoSum(vector<int>& price, int target) 
    {
        // 1、数据初始化
        int left = 0, right = price.size() - 1;
        // 2、利用双指针解决问题
        while(left < right)
        {
            int sum = price[left] + price[right];
            if(sum < target) ++left;
            else if(sum > target) --right;
            else return {price[left], price[right]};
        }
        // 题目没有明确说明没有结果的话会怎么样，那么该题的测试用例应该都是有结果的
        // 为了照顾编译器要求一定要返回一个结果，所以我们最后返回一个空数组即可
        return {};
    }
};
/*
- 时间复杂度：O(n)
- 空间复杂度：O(1)
*/

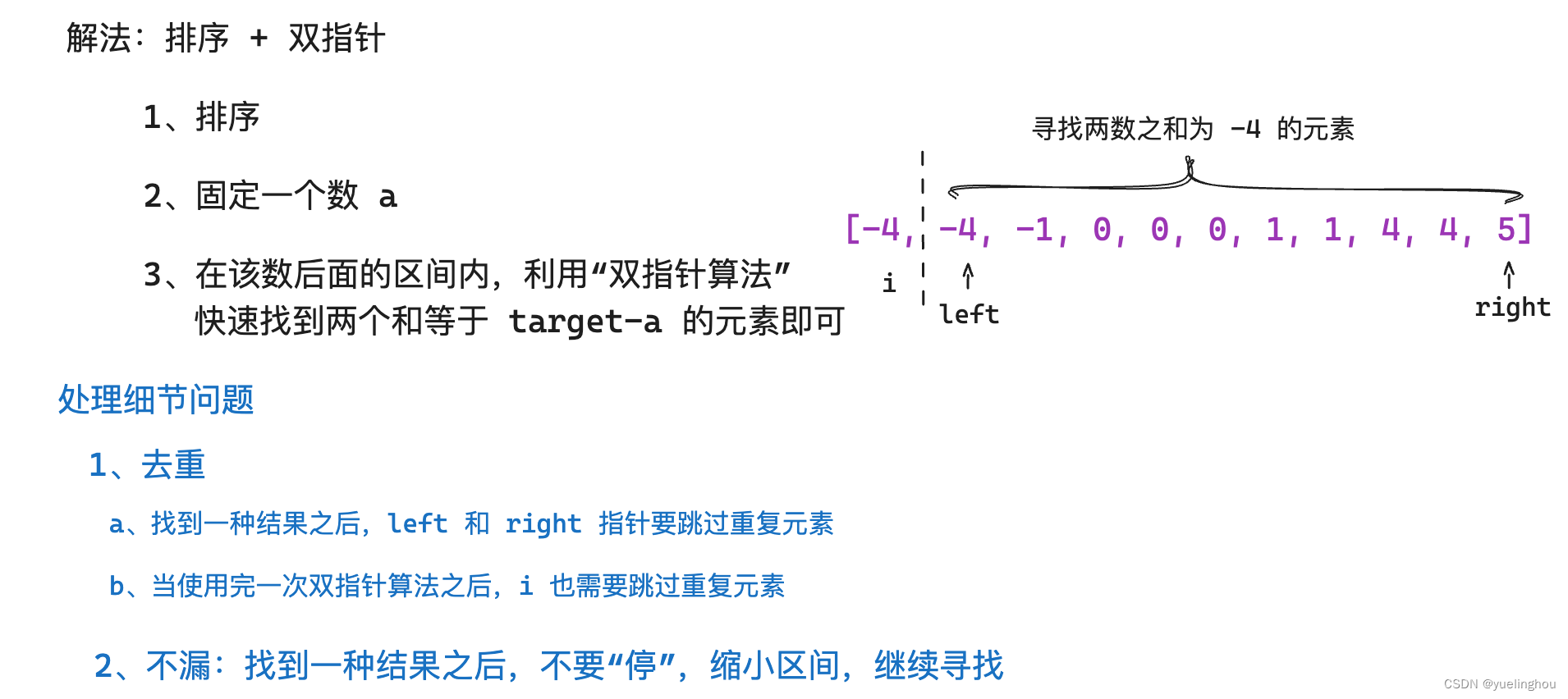
7. 三数之和

在这里插入图片描述

算法原理
在这里插入图片描述

代码编写

class Solution 
{
public:
    vector<vector<int>> threeSum(vector<int>& nums) 
    {
        // 1、初始化
        int n = nums.size();
        vector<vector<int>> ret;
        // 2、排序
        sort(nums.begin(), nums.end());
        // 3、依次固定一个数
        for(int i = 0; i < n - 2;)
        {
            // 4、双指针算法找到两数之和等于 aim 的元素
            int left = i + 1, right = n - 1, aim = -nums[i];
            while(left < right)
            {
                int sum = nums[left] + nums[right];
                if(sum < aim) ++left;
                else if(sum > aim) --right;
                else 
                {
                    ret.push_back( {nums[i], nums[left], nums[right]} );
                    ++left, --right; // 保证 left、right 选择的元素不漏
                    // 对 left、right 已经选择过的元素去重
                    while(left < right && nums[left] == nums[left - 1]) ++left;
                    while(left < right && nums[right] == nums[right + 1]) --right;
                }
            }
            // 保证 i 选择的元素不漏
            ++i; 
            // 对 i 已经选择过的元素去重
            while(i < n - 2 && nums[i] == nums[i - 1]) ++i;
        }
        // 5、返回最终结果
        return ret;
    }
};
/*
- 时间复杂度：O(n^2)
- 空间复杂度：O(1)
*/

8. 四数之和

在这里插入图片描述

算法原理
在这里插入图片描述

代码编写

class Solution 
{
public:
    vector<vector<int>> fourSum(vector<int>& nums, int target) 
    {
        // 1、初始化
        int n = nums.size();
        vector< vector<int> > ret;
        // 2、排序
        sort(nums.begin(), nums.end());
        // 3、依次固定一个数，然后使用“三数之和”解决问题
        for(int i = 0; i < n - 3;) 
        {
            // 4、再依次固定一个数，然后使用“双指针”解决问题
            for(int j = i + 1; j < n - 2;) 
            {
                int left = j + 1, right = n - 1;
                double aim = (double)target - nums[i] - nums[j];
                // 5、双指针算法找到两数之和等于 aim 的元素
                while(left < right)
                {
                    double sum = nums[left] + nums[right];
                    if(sum < aim) ++left;
                    else if(sum > aim) --right;
                    else
                    {
                        ret.push_back( {nums[i], nums[j], nums[left], nums[right]} );
                        ++left, --right; // 保证 left、right 选择的元素不漏
                        // 对 left、right 已经选择过的元素去重
                        while(left < right && nums[left] == nums[left - 1]) ++left;
                        while(left < right && nums[right] == nums[right + 1]) --right;
                    }
                }
                // 保证 j 选择的元素不漏
                ++j;
                // 对 j 已经选择过的元素去重
                while(j < n - 2 && nums[j] == nums[j - 1]) ++j;
            }
            // 保证 i 选择的元素不漏
            ++i;
            // 对 i 已经选择过的元素去重
            while(i < n - 3 && nums[i] == nums[i - 1]) ++i;
        }
        // 6、返回最终结果
        return ret;
    }
};
/*
- 时间复杂度：O(n^3)
- 空间复杂度：O(1)
*/

专题二：滑动窗口

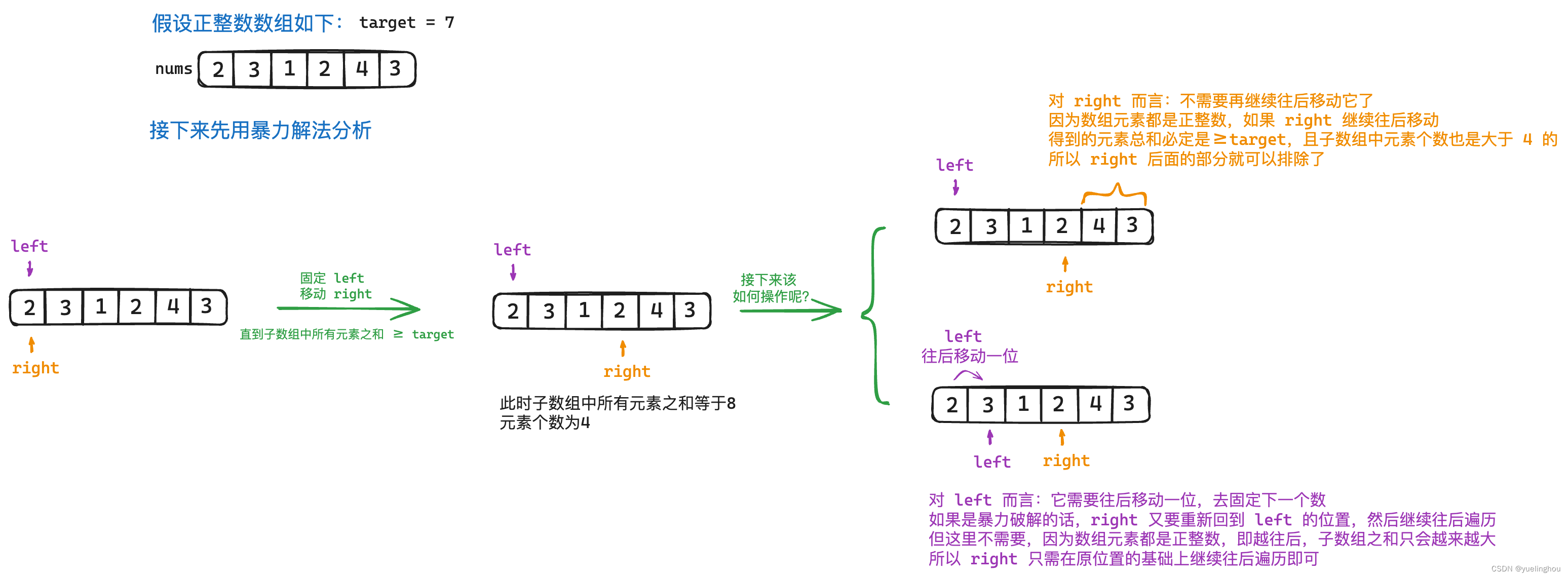
1. 长度最小的子数组

在这里插入图片描述

算法原理
在这里插入图片描述

代码编写

class Solution 
{
public:
    int minSubArrayLen(int target, vector<int>& nums) 
    {
        // 1、初始化
        int n = nums.size();
        int minLength = INT_MAX;
        // 2、使用滑动窗口解决问题
        for(int left = 0, right = 0, sum = nums[0]; right < n;)
        {
            if(sum >= target) 
            {
                minLength = min(minLength, right - left + 1);
                sum -= nums[left++];
            }
            else 
            {
                if(++right < n)
                    sum += nums[right];
            }
        }
        // 3、返回值
        return minLength == INT_MAX ? 0 : minLength;
    }
};
/*
- 时间复杂度：O(n)
- 空间复杂度：O(1)
*/

2. 无重复字符的最长字串

在这里插入图片描述

算法原理
在这里插入图片描述

代码编写

class Solution 
{
public:
    int lengthOfLongestSubstring(string s) 
    {
        // 1、初始化
        int n = s.size();
        vector<int> count(256);
        int left = 0, right = 0, ret = 0;
        // 2、滑动窗口
        int length = 0; //用来记录窗口长度
        while(right < n)
        {
            if(!count[s[right]]) //进窗口
            {
                ++count[s[right]];
                ++length;
                ++right;
                ret = max(ret, length); //更新结果
            }
            else //出窗口
            {
                --count[s[left]];
                --length;
                ++left;
            }
        }
        // 3、返回值
        return ret;
    }
};
/*
- 时间复杂度：O(n)
- 空间复杂度：O(1)
*/

3. 最大连续1的个数 III

在这里插入图片描述

算法原理
在这里插入图片描述

代码编写

class Solution 
{
public:
    int longestOnes(vector<int>& nums, int k) 
    {
        // 1、初始化
        int n = nums.size();
        int ret = INT_MIN;
        // 2、滑动窗口
        int left = 0, right = 0;
        int length = 0; // 当前子数组中最长连续 1 的长度
        int zero = 0;  // 当前子数组中 0 出现的次数
        while(right < n)
        {
            if(nums[right] != 0) // nums[right] 非 0，此时 right 一定入窗口
            {
                ret = max(ret, ++length);
                ++right;
            }
            else
            {
                if(zero + 1 <= k) 
                {
                    ret = max(ret, ++length);
                    ++zero;
                    ++right;
                }
                else
                {
                    if(nums[left++] == 0)  --zero;
                    --length;
                }
            }
        }
        // 3、返回值
        return ret;
    }
};
/*
- 时间复杂度：O(n)
- 空间复杂度：O(1)
*/

4. 将 x 减到 0 的最小操作数

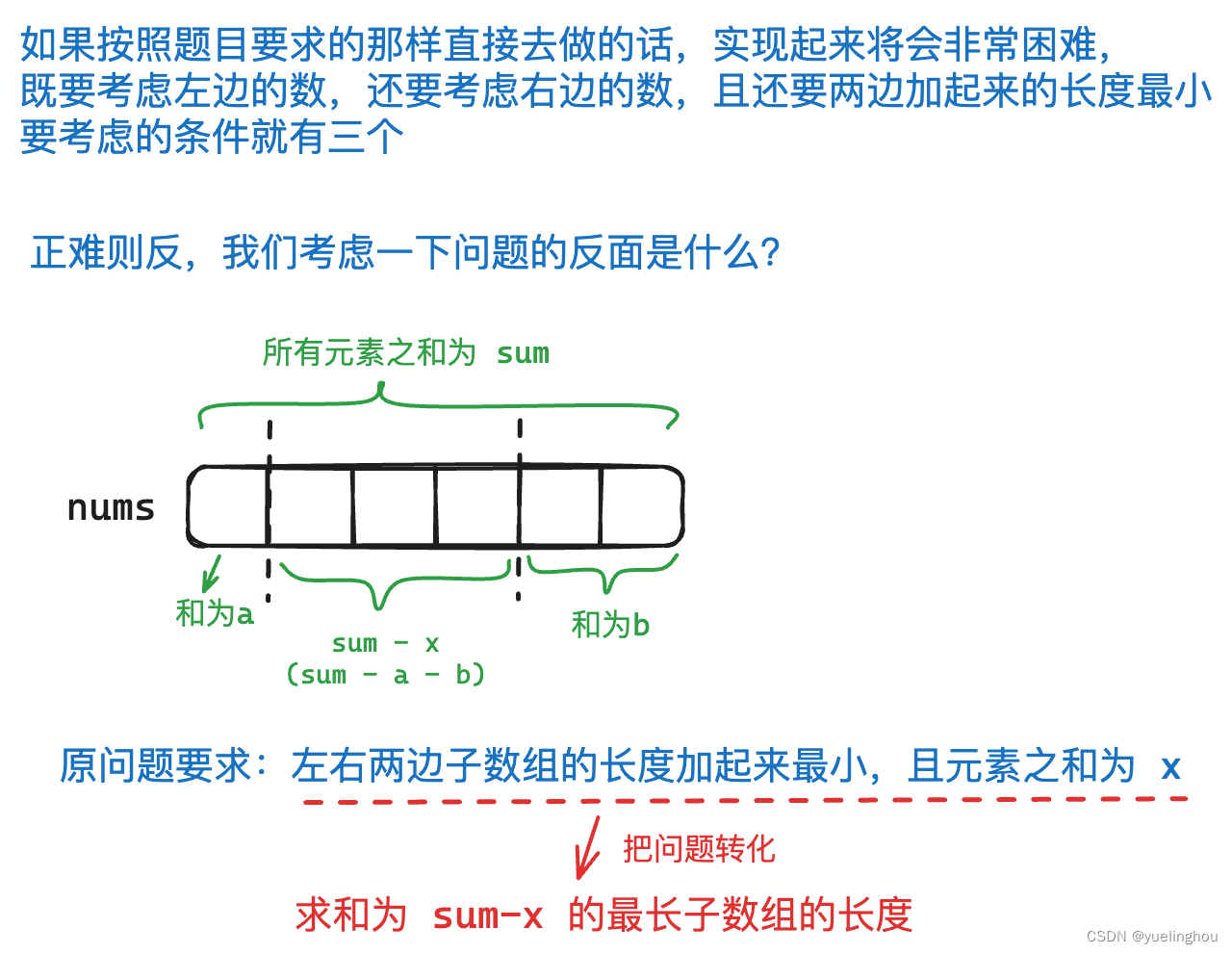
在这里插入图片描述

题目解析
在这里插入图片描述

算法原理
在这里插入图片描述

代码编写

class Solution 
{
public:
    int minOperations(vector<int>& nums, int x) 
    {
        // 1、初始化
        int sum = 0;
        for(const auto e : nums) sum += e;
        int target = sum - x;
        // 2、细节处理(数组中所有元素都大于0，所以 target 小于 0 是不存在的)
        if(target < 0) return -1;
        // 3、滑动窗口
        int ret = -1;
        for(int left = 0, right = 0, tmp = 0; right < nums.size();)
        {
            // 进窗口
            tmp += nums[right++];
            // 出窗口
            while(tmp > target) tmp -= nums[left++];
            // 更新结果
            if(tmp == target) ret = max(ret, right - left);
        }
        // 4、返回结果
        return ret == -1 ? ret : nums.size() - ret;
    }
};
/*
- 时间复杂度：O(n)
- 空间复杂度：O(1)
*/

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1243327.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【尚跑】2023泾阳半程马拉松144 PB完赛

【尚跑】2023泾阳半程马拉松144 PB完赛

1、赛事背景 来到泾阳&#xff0c;就来到了中国大地原点&#xff1b; 来到泾阳&#xff0c;就来到了陕西的“白菜心心”&#xff1b; 来到泾阳&#xff0c;就来到了具有2000多年的历史长河&#xff1b; 泾河水缓缓流&#xff0c;流过郑国渠&#xff1b; 泾河水缓缓流&…
阅读更多...
线程提交线程到线程池，有几种方式，哪一种方式是工作中不能使用的，无法捕捉异常，线程池的拒绝策略，线程池的提交方式

线程提交线程到线程池，有几种方式，哪一种方式是工作中不能使用的，无法捕捉异常，线程池的拒绝策略，线程池的提交方式

线程池的工作原理 JDK中提交线程到线程池&#xff0c;有几种方式&#xff0c;哪一种方式是工作中不能使用的&#xff0c;无法捕捉异常 两种提交任务的方法 ExecutorService 提供了两种提交任务的方法&#xff1a; execute()&#xff1a;提交不需要返回值的任务 submit()&a…
阅读更多...
gRPC之gRPC负载均衡(客户端负载均衡)(etcd)

gRPC之gRPC负载均衡(客户端负载均衡)(etcd)

1、gRPC负载均衡(客户端负载均衡)(etcd) 本篇将基于etcd的服务发现前提下&#xff0c;介绍如何实现gRPC客户端负载均衡。 1.1 gRPC负载均衡 gRPC官方文档提供了关于gRPC负载均衡方案Load Balancing in gRPC https://github.com/grpc/grpc/blob/master/doc/load-balancing.m…
阅读更多...
二十一、文档操作

二十一、文档操作

目录 一、添加文档 1、编写代码 2、运行并查看 二、查询文档 1、编写代码 2、运行并查看 三、删除文档 1、编写代码 2、运行并查看 四、修改文档 方式一&#xff1a;全量修改&#xff0c;会删除旧文档&#xff0c;添加新文档 方式二&#xff1a;局部修改。增量修改&…
阅读更多...
TCP /UDP协议的 socket 调用的过程

TCP /UDP协议的 socket 调用的过程

在传输层有两个主流的协议 TCP 和 UDP&#xff0c;socket 程序设计也是主要操作这两个协议。这两个协议的区别是什么呢&#xff1f;通常的答案是下面这样的。 TCP 是面向连接的&#xff0c;UDP 是面向无连接的。TCP 提供可靠交付&#xff0c;无差错、不丢失、不重复、并且按序…
阅读更多...
mybatis 语法使用各种踩坑（持续更新中。。。）

mybatis 语法使用各种踩坑（持续更新中。。。）

1、大小写命名&#xff1a;这个别说了&#xff0c;都是泪。 2、联表查询查询&#xff0c;多条合成一条&#xff0c;不生效的原因 博主各种检查关联关系和字段大小写&#xff0c;本来是4条数据最后合成一条数据&#xff0c;死活给你直接返回了4条数据&#xff0c;而且每个类似p…
阅读更多...
Llama 2 70B nvidia model learning tranformer

Llama 2 70B nvidia model learning tranformer

website
阅读更多...
实现二叉搜索树的查找、插入和删除功能（思路+图文+代码详解）

实现二叉搜索树的查找、插入和删除功能（思路+图文+代码详解）

文章目录 二叉搜索树一、搜索树1.二叉搜索树的查找2.二叉搜索树的插入3.二叉搜索树的删除4.性能分析 二叉搜索树 HashMap和HashSet的底层是一个哈希表 TreeMap 和TreeSet底层是一棵搜索树&#xff08;红黑树&#xff09; 涉及到一些搜索查找的场景可以调用Map和Set接口 一、…
阅读更多...
SPSS多元对应分析

SPSS多元对应分析

前言&#xff1a; 本专栏参考教材为《SPSS22.0从入门到精通》&#xff0c;由于软件版本原因&#xff0c;部分内容有所改变&#xff0c;为适应软件版本的变化&#xff0c;特此创作此专栏便于大家学习。本专栏使用软件为&#xff1a;SPSS25.0 本专栏所有的数据文件请点击此链接下…
阅读更多...
IDEA、PHPSTORM 在命令行中进行 PHP debug

IDEA、PHPSTORM 在命令行中进行 PHP debug

然在终端执行控制器的方法php yii test/ab 即可看到触发debug 调试
阅读更多...
管理类联考——英语二——备考 100 句涵盖所有词汇

管理类联考——英语二——备考 100 句涵盖所有词汇

全中 在海里的这个地区&#xff0c;熊猫们喜欢就着苏打碗豆喝茶。而大洋州的民兵则喜欢经过半岛&#xff0c;带着编剧本的公式上餐厅去。附件的电影院里有额外的歌剧和香蕉&#xff0c;这一时代的斑马们被外面的天线所吸引。实验室里的蟹想用它的肋骨去戳四肢象灯炮的小羊。但…
阅读更多...
虚拟机VMware上安装Ubuntu系统（详细图文教程）

虚拟机VMware上安装Ubuntu系统（详细图文教程）

关于虚拟机VMware的安装教程&#xff0c;学者看我另外一篇博客&#xff1a;VMware详细安装教程 目录 一、Ubuntn系统准备二、VMware上安装Ubuntn系统2.1 答疑 三、导入Ubuntu系统四、总结 一、Ubuntn系统准备 先下载好Ubuntn系统&#xff0c;这里我提供一个&#xff0c;下载链…
阅读更多...
基于51单片机设计的人体温度检测与存储系统

基于51单片机设计的人体温度检测与存储系统

一、前言 随着科技的快速发展和人们对健康生活的追求，准确、便捷的体温检测成为日常生活中的重要需求。在当前全球健康环境下，特别是在一些公共场合和家庭中，快速筛查体温以预防疾病传播变得至关重要。基于这一需求，当前设计了基于51单片机的温度检测与存储系统。 传统体…
阅读更多...
外部 prometheus监控k8s集群资源（pod、CPU、service、namespace、deployment等）

外部 prometheus监控k8s集群资源（pod、CPU、service、namespace、deployment等）

prometheus监控k8s集群资源 一&#xff0c;通过CADvisior 监控pod的资源状态1.1 授权外边用户可以访问prometheus接口。1.2 获取token保存1.3 配置prometheus.yml 启动并查看状态1.4 Grafana 导入仪表盘 二&#xff0c;通过kube-state-metrics 监控k8s资源状态2.1 部署 kube-st…
阅读更多...
电子学会C/C++编程等级考试2023年03月（一级）真题解析

电子学会C/C++编程等级考试2023年03月（一级）真题解析

C/C++等级考试（1~8级）全部真题・点这里 第1题：字符长方形 给定一个字符，用它构造一个长为4个字符，宽为3个字符的长方形，可以参考样例输出。 时间限制：1000 内存限制：65536输入 输入只有一行， 包含一个字符。输出 该字符构成的长方形，长4个字符，宽3个字符。样例输入…
阅读更多...
物联网AI MicroPython学习之语法 I2S音频总线接口

物联网AI MicroPython学习之语法 I2S音频总线接口

学物联网&#xff0c;来万物简单IoT物联网&#xff01;&#xff01; I2S 介绍 模块功能: I2S音频总线驱动模块 接口说明 I2S - 构建I2S对象 函数原型&#xff1a;I2S(id, sck, ws, sd, mode, bits, format, rate, ibuf)参数说明&#xff1a; 参数类型必选参数&#xff1f…
阅读更多...
linux centos上安装python3.11.x详细完整教程

linux centos上安装python3.11.x详细完整教程

一. 安装步骤 注意&#xff1a; 1、安装python3.11的其他版本替换下面的版本信息即可。(如想安装3.11.5将案例中的3.11.0替换成3.11.5即可) #下载最新的软件安装包 wget https://www.python.org/ftp/python/3.11.0/Python-3.11.0.tgz#解压缩安装包 tar -xzf Python-3.11.0.tg…
阅读更多...
【OpenCV实现图像：制作酷炫的动画效果】

【OpenCV实现图像：制作酷炫的动画效果】

文章目录 概要生成背景图添加点动画添加文本显示小结 概要 首先&#xff0c;通过导入必要的库&#xff0c;包括NumPy用于数学运算和Matplotlib库用于数据可视化。随后&#xff0c;创建图形和轴&#xff0c;初始化点的位置&#xff0c;以及编写初始化函数和更新函数。 初始化函…
阅读更多...
轻松搞定HTTP接口测试，JMeter让你事半功倍！

轻松搞定HTTP接口测试，JMeter让你事半功倍！

jmeter-http接口测试脚本 jmeter进行http接口测试的主要步骤&#xff08;1.添加线程组 2.添加http请求 3.在http请求中写入接口的URL&#xff0c;路径&#xff0c;请求方式&#xff0c;参数 4.添加查看结果树 5.调用接口&#xff0c;查看返回值&#xff09; 针对接口添加heade…
阅读更多...
2024东北师范大学计算机考研分析

2024东北师范大学计算机考研分析

24计算机考研|上岸指南 东北师范大学 信息科学与技术学院位于长春净月国家高新技术产业开发区&#xff0c;毗邻风光秀美的净月潭国家森林公园。 信息科学与技术学院由原“计算机科学与信息技术学院”和“信息与软件工程学院”于2017年根据学校事业发展需要整合形成。学院设有…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023