文章目录
- 二叉搜索树
- 一、搜索树
- 1.二叉搜索树的查找
- 2.二叉搜索树的插入
- 3.二叉搜索树的删除
- 4.性能分析
二叉搜索树
-
HashMap和HashSet的底层是一个哈希表
-
TreeMap 和TreeSet底层是一棵搜索树(红黑树)
-
涉及到一些搜索查找的场景可以调用Map和Set接口
一、搜索树
二叉搜素树 又叫 二叉排序树
1.要么是空树
2.如果左子树不为空,则左子树上所有节点的值都小于根节点的值
3.如果右子树不为空,则右子树上所有节点的值都大于根节点的值
4.它的左右子树也是二叉搜索树
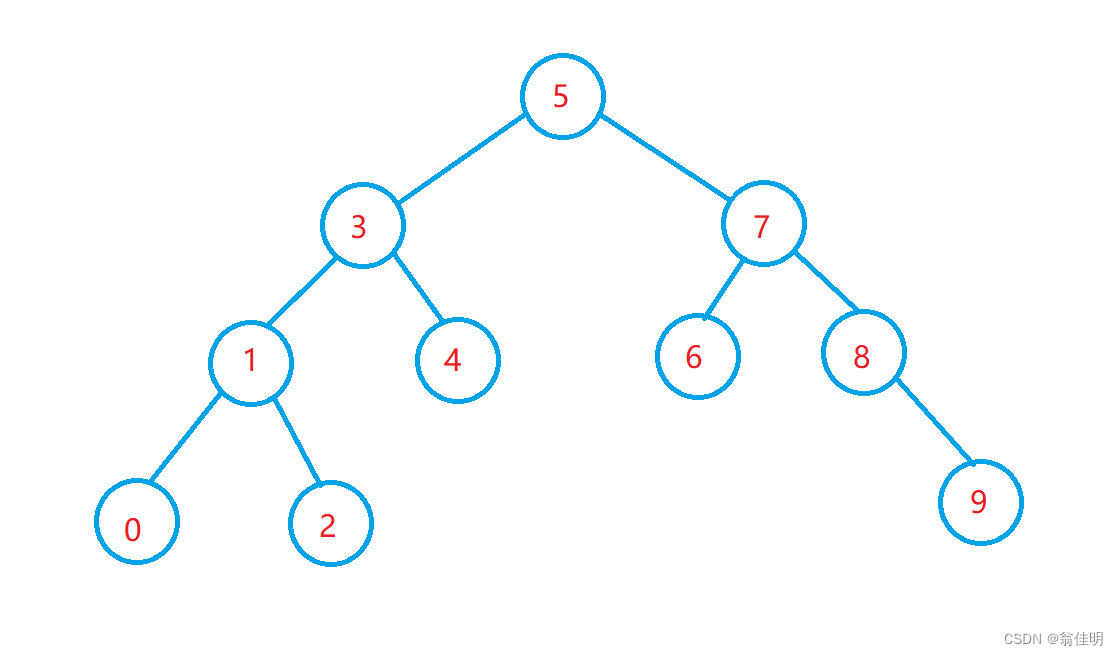
1.二叉搜索树的查找
-
将要查找的值,和根节点比较
-
比根节点小的在左树找,比根节点大的在右树找
最坏情况:按单分支树找, 为树的高度 N
最好情况:完全二叉树、满二叉树,树的高度为log2N,效率最高
为了解决单分支树的问题,采用AVL树解决。
- AVL树:高度平衡的二叉搜索树,保证高度一直平衡(左右高度差不超过1),需要不断进行旋转,来保持平衡
- 红黑树:加入了颜色,减少了旋转
public class BinarySearchTree {
static class TreeNode {//静态内部类
public int val;
public TreeNode left;
public TreeNode right;
public TreeNode(int val) {
this.val = val;
}
}
public TreeNode root = null;
/**
* 查找二叉搜索树中指定的val值
*
* @param val
* @return
*/
public TreeNode find(int val) {
TreeNode cur = root;
while (cur != null) {
if (cur.val == val) {
return cur;
} else if (cur.val < val) {
cur = cur.left;
} else {
cur = cur.right;
}
}
return null;
}
- 1.设cur结点为root位置
- 2.cur的val如果小于目标val,cur移动到左子树
- 3.cur 的val如果大于目标val,cur移动到右子树
2.二叉搜索树的插入
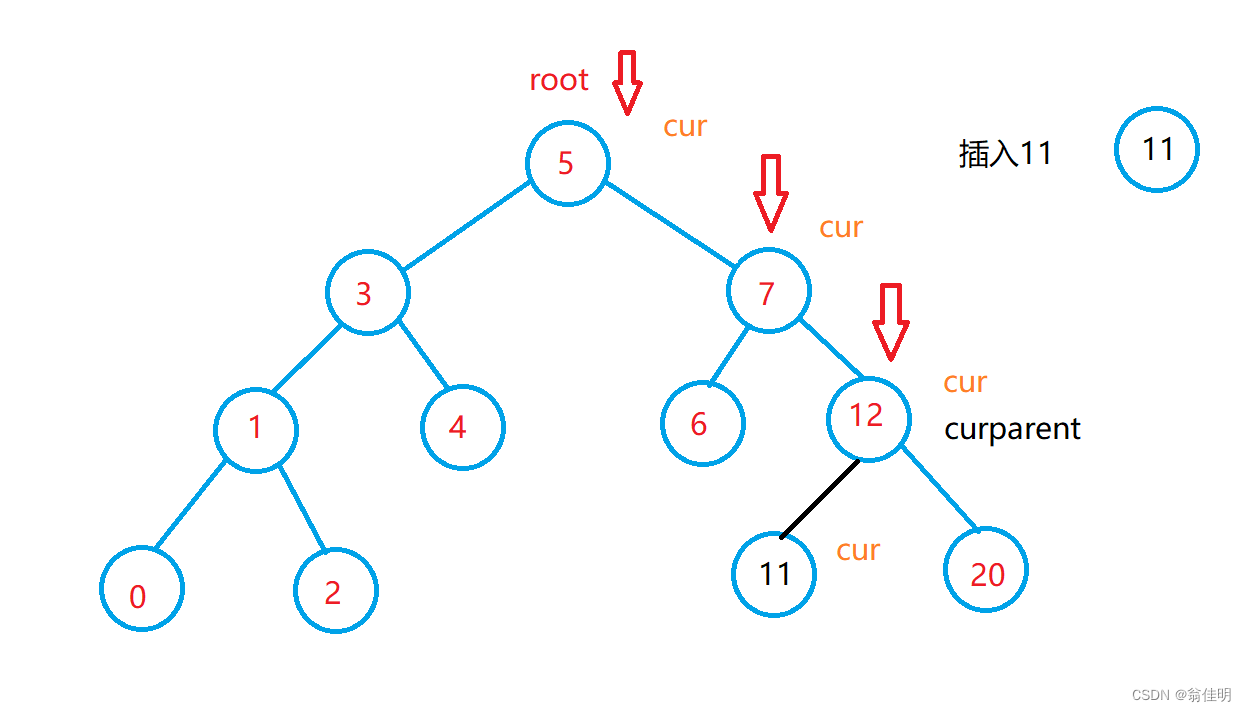
- 1.如果是空树(root==null),直接插入根的位置
- 2.如果不是空树,按照查找的逻辑找到要插入的位置,插入新结点
- 3.都插入到了叶子结点,也就是cur为空时的位置
- 4.所以要记录一个cur的双亲结点,方便cur插入数据
/**
* 插入一个数据
*
* @param val
*/
public void insert(int val) {
//root为空
if (root == null) {
root = new TreeNode(val);
return;
}
//root不为空
TreeNode cur = root;
TreeNode parent = null;
//找到cur为空的位置
while (cur != null) {
if (cur.val < val) {
parent = cur;
cur = cur.right;
} else if (cur.val > val) {
parent = cur;
cur = cur.left;
} else {
return;
}
}
//根据判断双亲结点的值来决定插入那个叶子结点
TreeNode node = new TreeNode(val);
if (val < parent.val) {
parent.left = node;
} else {
parent.right = node;
}
}
public void inorder(TreeNode root) {
if (root == null) {
return;
}
inorder(root.left);
System.out.print(root.val + " ");
inorder(root.right);
}
3.二叉搜索树的删除
要删除的位置为cur,它的双亲结点为parent
-
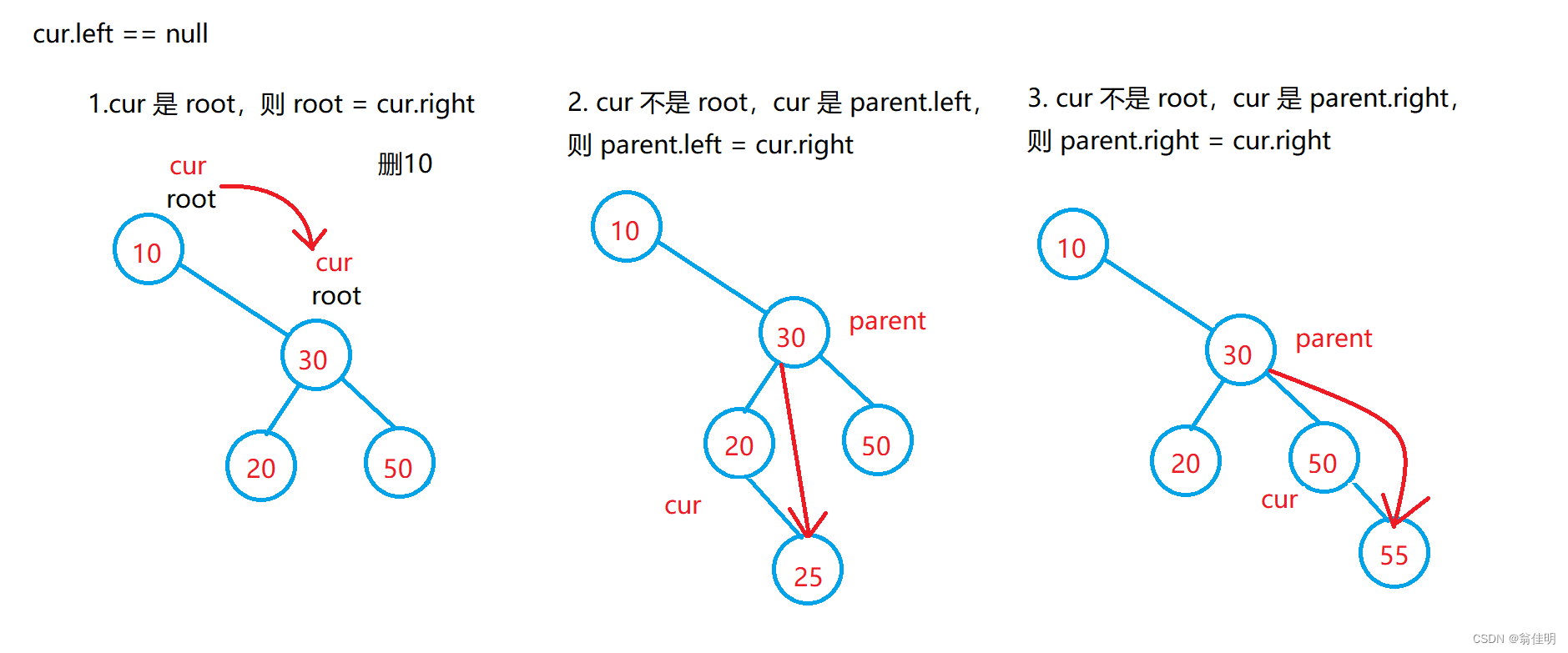
1.cur左结点为空:cur.left == null
1.cur为根节点,cur没有左树,根节点移动到它的右树上
2.cur不是根节点,此时cur为双亲结点的左结点,cur没有左树,双亲结点的左结点连上cur的右结点 parent.left = cur.right
3.cur不是根节点,此时cur为双亲结点的右结点,cur没有左树,双亲结点的右结点连上cur的右结点 parent.right = cur.right
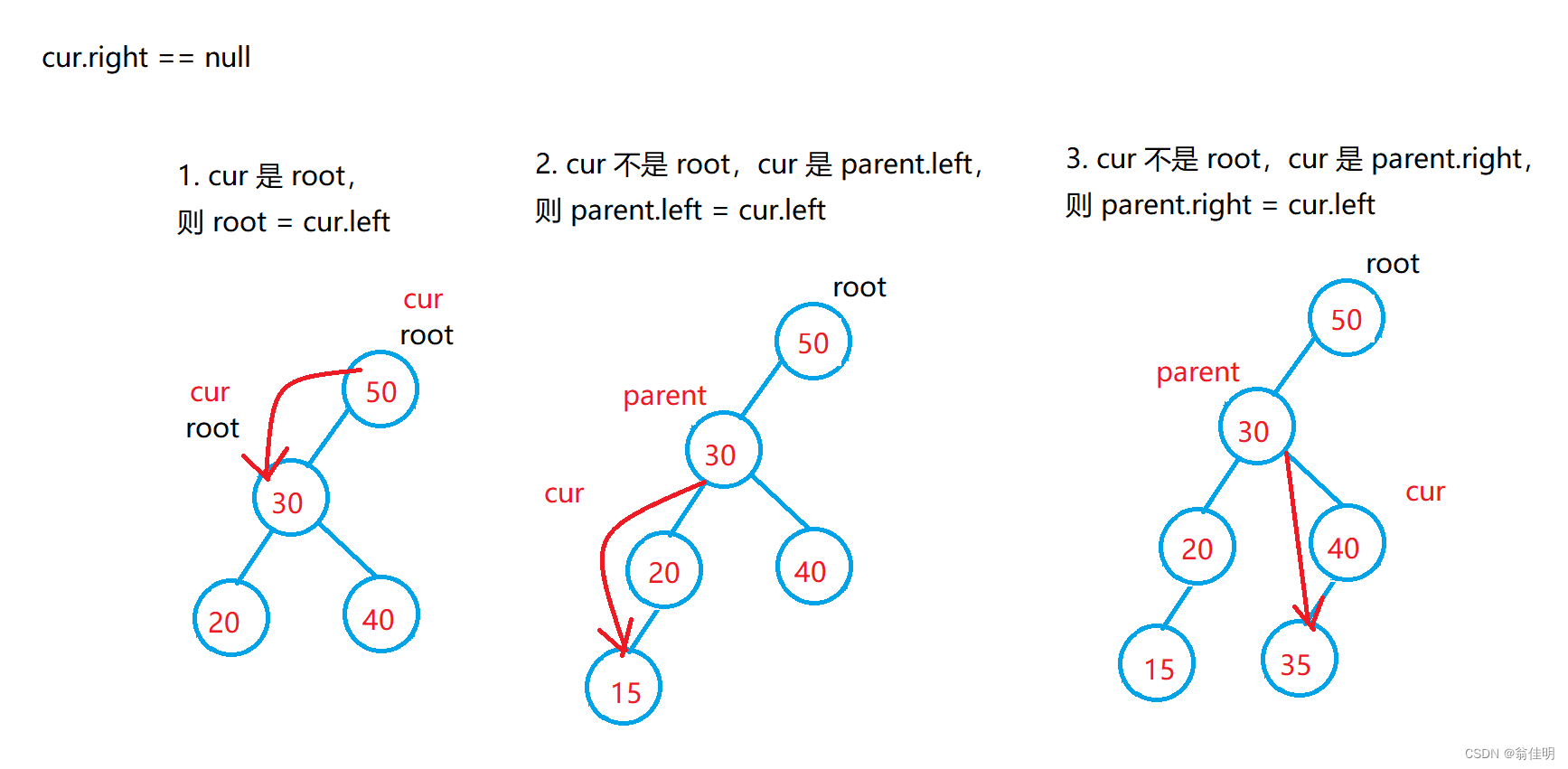
- 2.cur右结点为空:cur.right == null
1.cur为根节点,cur没有右子树,根节点移动到cur的左子树上
2.cur不是根节点,cur是双亲结点的左结点,cur没有右结点,双亲结点的左结点连上cur的左结点
3.cur不是根节点,cur是双亲结点的右结点,cur没有右结点,双亲结点的右结点连上cur的左结点
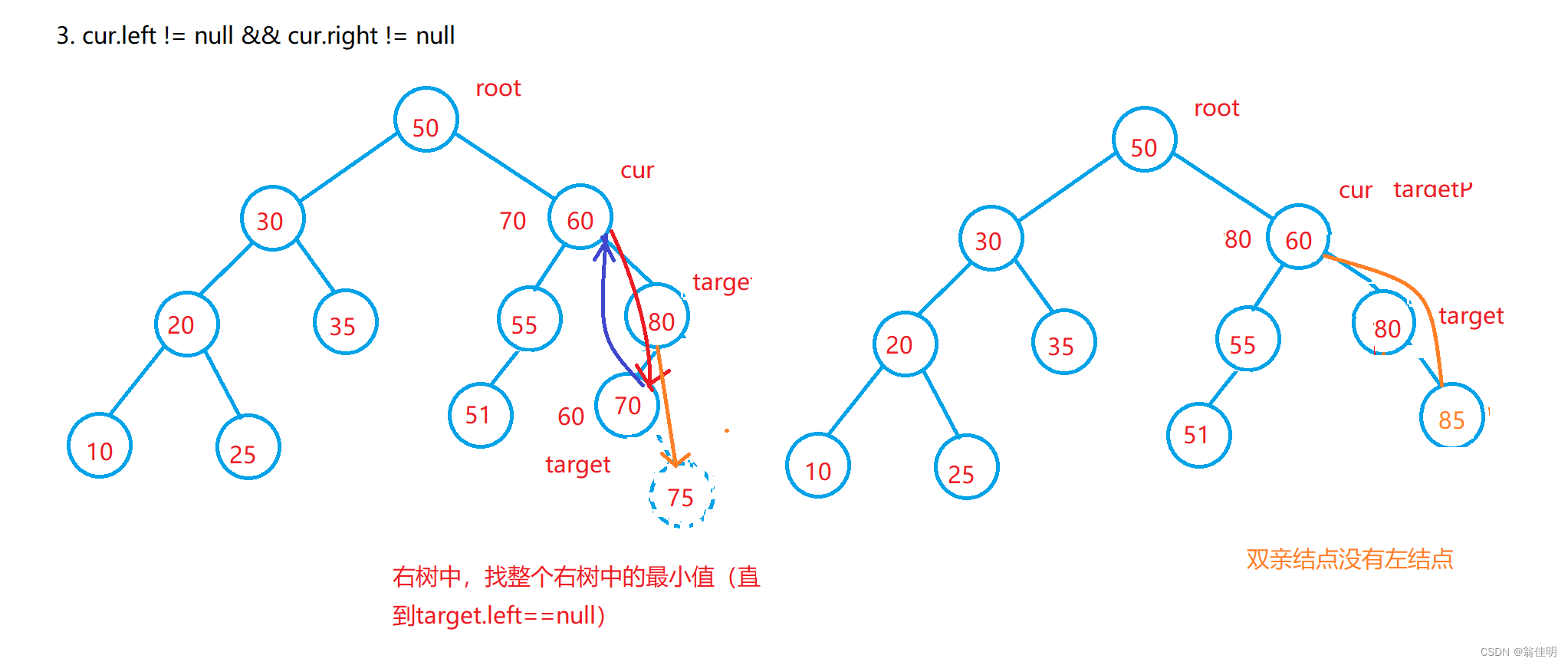
3.左右结点都不为空:cur.left != null && cur.right != null
1.替换法进行删除,在cur的右子树中,找到该子树的最小值,和要删除的值交换
2.最后删除那个替换的结点,维护了二叉搜索树
3.替换的结点在它双亲结点的左边,没有左子树,target.left==nulll,如果有右子树,target双亲结点的左结点连接target的右结点(target的右结点都比target大),没有右子树,连接的是空值
4.替换的结点在它双亲结点的右边(双亲结点没有左结点),target双亲结点的右结点连接target的右结点
/**
* 删除值为val的结点
*
* @param val
* @return
*/
public void remove(int val) {
TreeNode cur = root;
TreeNode parent = null;
//找到cur结点的位置
while (cur != null) {
if (cur.val == val) {
removeNode(cur, parent);
return;
} else if (val < cur.val) {
parent = cur;
cur = cur.left;
} else {
parent = cur;
cur = cur.right;
}
}
}
/**
* 删除结点的分类情况
*
* @param cur
* @param parent
*/
private void removeNode(TreeNode cur, TreeNode parent) {
if (cur.left == null) {
//cur的左结点为空
if (cur == root) {
root = cur.right;
} else if (cur == parent.left) {
parent.left = cur.right;
} else {
parent.right = cur.right;
}
} else if (cur.right == null) {
//cur的右结点为空
if (cur == root) {
root = cur.left;
} else if (cur == parent.left) {
parent.left = cur.left;
} else {
parent.right = cur.left;
}
} else {
//cur的左右结点都不为空
TreeNode target = cur.right;//在右树中找最小值
TreeNode targetParent = cur;
while (target.left != null) {
targetParent = target;
target = target.left;
}//找最小值
cur.val = target.val;//替换
if (target == targetParent.left) {
targetParent.left = target.right;
//目标值在双亲结点的左边
} else {
targetParent.right = target.right;
//目标值在双亲结点的右边
}
}
}
4.性能分析
插入和删除操作都必须先查找,查找效率代表了二叉搜索树中各个操作的性能
- 即结点越深,则比较次数越多
- 插入的次序不同,可能得到不同结构的二叉搜索树
最好情况:二叉搜索树为完全二叉树,平均计较次数:log2N
最坏情况:二叉树退化成单分支树,平均比较次数为 N/2
点击移步博客主页,欢迎光临~