🏆作者提出了一个单目相机的视频序列进行深度估计与运动估计,作者的方法是完全无监督的,端到端的学习,作者使用了单视角深度网络和多姿态网络,提出了一个图像(predict)与真实的下一帧(goundturth)计算loss,作为无监督的依据,实现无监督学习。使用KITTI数据集证明了他们的有效性:1.合成的深度图与监督学习的方法是可比的;2. 在可比较的输入设置下,姿势估计与已建立的SLAM系统相比性能优越
文章目录
- 原理分析
- 实施细节
- 限制条件

会议/期刊:CVPR2017
论文题目:《Unsupervised Learning of Depth and Ego-Motion from Video》
论文链接:Unsupervised Learning of Depth and Ego-Motion from Video (arxiv.org)
开源代码:tinghuiz/SfMLearner: An unsupervised learning framework for depth and ego-motion estimation from monocular videos (github.com)
原理分析
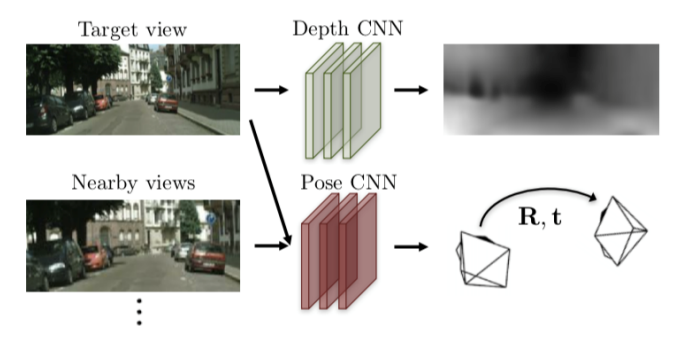
SfMLearner算法的原理:
-
利用Depth CNN对当前图像进行深度估计,得到当前图像的深度图
-
将相邻帧(包括当前帧、上一帧、下一帧)输入Pose CNN,得到旋转矩阵R和平移矩阵T,预测相机的位姿变化
-
将1、2得到的当前深度图和相邻帧对的R、T矩阵,计算出当前帧和下一帧的映射关系,然后将当前帧warp到下一帧
深度学习论文中的warp是指什么?
warp就是将一个图像上的点变换到另一张图像上 -
最后将warp出来的图像(predict)与真实的下一帧(goundturth)计算loss,作为无监督的依据,实现无监督学习
实施细节
-
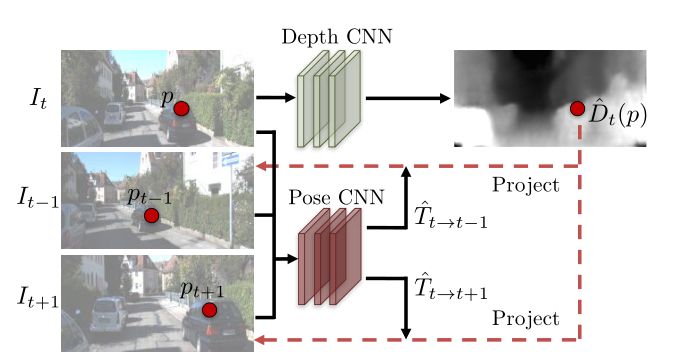
将当前帧 𝐼 𝑡 𝐼_𝑡 It 输入到 Depth CNN 并预测出当前帧的深度图 D t D_t Dt
-
将其与邻近帧 𝐼 𝑡 − 1 𝐼_{𝑡−1} It−1 和 𝐼 𝑡 + 1 𝐼_{𝑡+1} It+1 组成邻近帧对 { 𝐼 𝑡 , 𝐼 𝑡 − 1 𝐼_𝑡 , 𝐼_{𝑡−1} It,It−1} 和 { 𝐼 𝑡 , 𝐼 𝑡 + 1 𝐼_𝑡 , 𝐼_{𝑡+1} It,It+1} 分别输入到 Pose CNN,预测出六个自由度的帧间位姿变化( r x , r y , r z , t x , t y , t z r_x,r_y,r_z,t_x,t_y,t_z rx,ry,rz,tx,ty,tz)。可以得到旋转矩阵 𝑹 和平移矩阵 𝒕。
其中 R 为 3*3 的旋转矩阵,𝑡 = [ 𝑡 𝑥 , 𝑡 𝑦 , 𝑡 𝑧 ] [𝑡_𝑥 , 𝑡_𝑦 , 𝑡_𝑧 ] [tx,ty,tz],𝑹 和 𝒕 合成为一个 4 *4 位姿变化矩阵 𝑇 𝑡 → 𝑠 𝑇_{𝑡→𝑠} Tt→s
T = ∣ R t 0 T 1 ∣ T=\left|\begin{array}{ll} \boldsymbol{R} & \boldsymbol{t} \\ \mathbf{0}^{T} & 1 \end{array}\right|{\color{Red} } T= R0Tt1 -
现在令 𝑝 𝑡 𝑝_𝑡 pt 为当前帧齐次像素坐标系下的坐标, 𝑝 𝑠 𝑝_𝑠 ps 为邻近 帧齐次像素坐标系下的坐标,根据 CNN 预测出的当前帧深度图 𝑫 𝑡 𝑫_𝑡 Dt 和帧间位姿 变化矩阵 𝑻 𝑡 → 𝑠 𝑻_{𝑡→𝑠} Tt→s,可以得到 𝐼 𝑡 , 𝐼 𝑠 𝐼_𝑡 , 𝐼_𝑠 It,Is 帧间映射关系:
p s ∼ K T t → s D t ( p t ) K − 1 p t p_{s} \sim \boldsymbol{K} \boldsymbol{T}_{t \rightarrow s} \boldsymbol{D}_{t}\left(p_{t}\right) \boldsymbol{K}^{-1} p_{t}{\color{Purple} } ps∼KTt→sDt(pt)K−1pt
其中𝑲 为相机内参矩阵,在本文实验中相机内参矩阵 𝑲 是已知的。下面对该映射关系公式进行分析当前帧的像素坐标系下坐标为 p t p_t pt,首先要将坐标从像素坐标系转换到成像坐标系,成像坐标系: 𝑝 𝑡 ’ 𝑝_𝑡 ’ pt’ ∼ 𝑲 − 1 𝑝 𝑡 𝑲^{−1}𝑝_𝑡 K−1pt,然后要将坐标从成像坐标系转换成相机坐标系,相机坐标系: 𝑝 𝑡 ’’ ∼ 𝑫 𝑡 ( 𝑝 𝑡 ) 𝑝 𝑡 ’ 𝑝_𝑡 ’’ ∼ 𝑫_𝑡 (𝑝_𝑡 )𝑝_𝑡 ’ pt’’∼Dt(pt)pt’,即 𝑝 𝑡 ’’ ∼ 𝑫 𝑡 ( 𝑝 𝑡 ) 𝑲 − 1 𝑝 𝑡 𝑝_𝑡 ’’ ∼ 𝑫_𝑡 (𝑝_𝑡 )𝑲^{−1}𝑝_𝑡 pt’’∼Dt(pt)K−1pt;此时坐标是三维坐标, 左乘位姿变化坐标就可以得到变换后的三维坐标: 𝑝 𝑠 ’ = 𝑻 𝑡 → 𝑠 𝑝 𝑡 ’’ 𝑝_𝑠 ’ = 𝑻_{𝑡→𝑠}𝑝_𝑡 ’’ ps’=Tt→spt’’;最后将变换后的三维坐标从相机坐标系转换到像素坐标系: 𝑝 𝑠 ∼ 𝑲 𝑝 𝑠 ’ 𝑝_𝑠 ∼ 𝑲𝑝_𝑠 ’ ps∼Kps’,即:
p s ∼ K T t → s D t ( p t ) K − 1 p t p_{s} \sim \boldsymbol{K} \boldsymbol{T}_{t \rightarrow s} \boldsymbol{D}_{t}\left(p_{t}\right) \boldsymbol{K}^{-1} p_{t} ps∼KTt→sDt(pt)K−1pt
参考链接:https://blog.csdn.net/qq_46058802/article/details/126227358
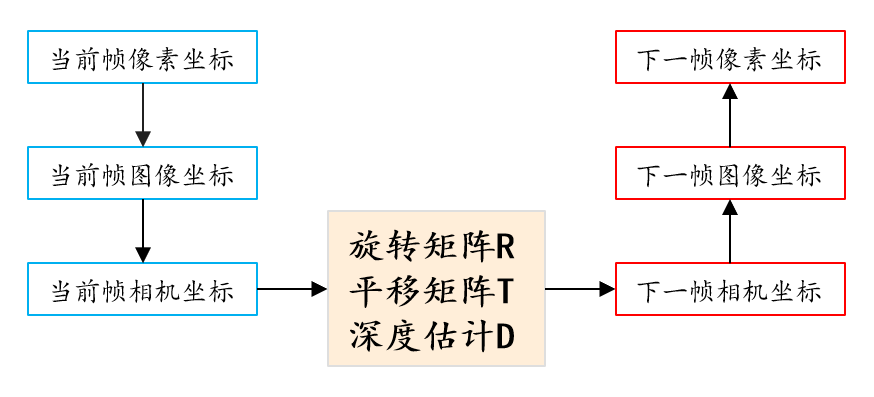
像素坐标系:像素坐标系的原点在左上角,并且单位为像素。比如一张224*224的图片,它的原点就在左上角的地方,然后x轴长224,y轴长224
成像坐标系:图像坐标系的坐标原点是成像平面的中心。例如:红色圈出来的区域,即是图像坐标系, 红色的原点,可以记为图像坐标系的原点
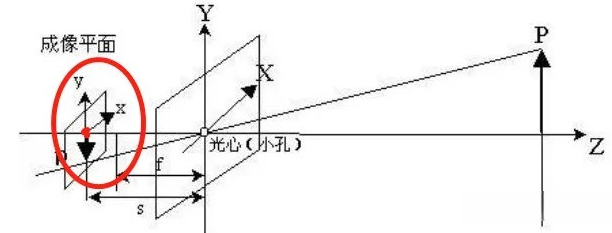
相机坐标系:下图红色坐标轴表示的,即是一个相机坐标。 与世界坐标非常像,只是世界坐标的原点是固定的,而相机坐标的原点,可以是任意的相机位置

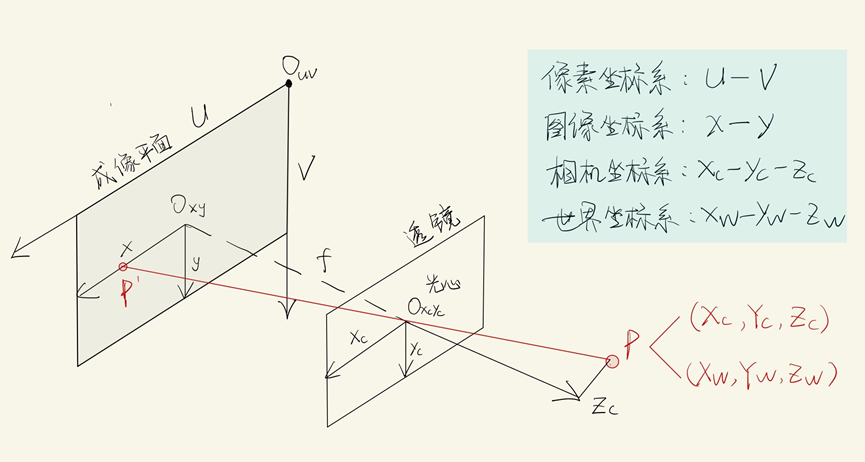
😎世界坐标、相机坐标、图像坐标和像素坐标的关系:
-
最后,得到了帧间的像素级映射关系后,我们就可以像光流一样进行帧间的 warp 操作
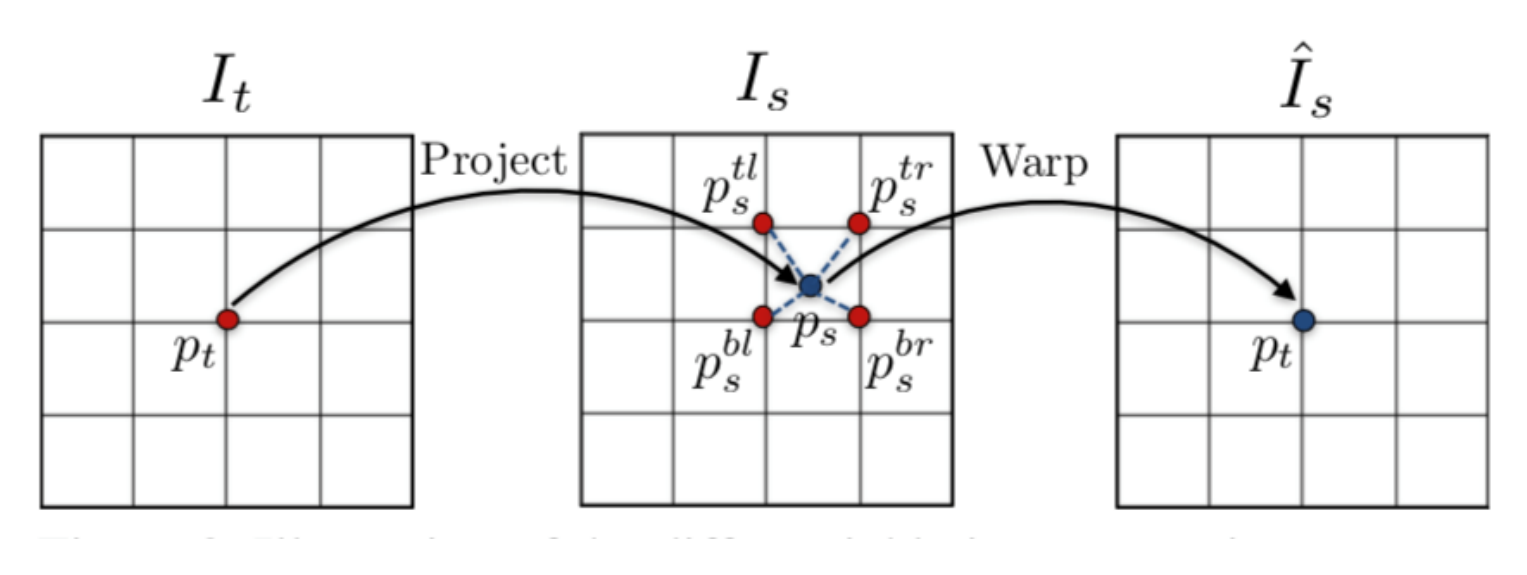
图中当前帧 𝐼 𝑡 𝐼_𝑡 It 上的像素点 𝑝 𝑡 𝑝_𝑡 pt 可以根据预测出的深度图和位姿变化矩阵,映射到 邻近帧 𝐼 𝑠 𝐼_𝑠 Is 上的 𝑝 𝑠 𝑝_𝑠 ps 点。该映射后的点不一定会刚好映射到 𝐼 𝑠 𝐼_𝑠 Is 的像素点上,而是大概率如图中一样,映射到由 𝐼 𝑠 𝐼_𝑠 Is 上的 𝑝 𝑠 𝑡 𝑙 𝑝^{𝑡𝑙}_𝑠 pstl , 𝑝 𝑠 𝑡 𝑟 𝑝^{𝑡𝑟}_𝑠 pstr , 𝑝 𝑠 𝑏 𝑙 𝑝^{𝑏𝑙} _𝑠 psbl , 𝑝 𝑠 𝑏 𝑟 𝑝^{𝑏𝑟}_𝑠 psbr 四个像素点组成的方格里。因 此这里和 DFF 的 warp 操作一样,要用双线性插值算法,求出 𝑝 𝑠 𝑝_𝑠 ps 的值,再将此值 返回给当前帧 𝐼 𝑡 𝐼_𝑡 It 的像素点 𝑝 𝑡 𝑝_𝑡 pt,从而完成 warp 操作
限制条件
-
图片中没有运动的对象,场景是静态的
-
目标视图和源视图之间没有遮挡
-
表面是朗伯型的,使得光一致性误差是有意义的
朗伯面是指在一个固定的照明角度下从所有视场方向上观测都具有相同亮度的表面,也就是反射亮度是一个常数。理想朗伯面是物体表面对入射光进行完全的反射,吸收率为0
为了提高对第一点因素(图片中没有运动的对象,场景是静态的)的抗性,作者额外训练了一个解释模型。输出一个像素级的粗糙蒙版(掩码),用来过滤掉会运动的物体,该 mask 用于 loss 计算的时候,对运动 的物体赋予一个较小的权重,对背景区域赋予一个较大的权重,以实现让网络自动屏蔽掉对场景变换估计有干扰的区域
在下图中,Pose CNN和解释模型共享前面的解码器流程,然后分别扩展到预测6-DOF相对姿势和多尺度可解释性掩码两个分支网络。经过红色网络的即是解释模型
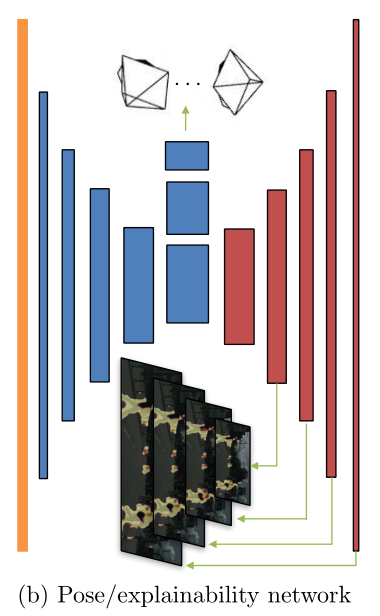
高亮的部分就是估计出来运动的对象,该块像素会被赋予一个比较低的权重计算loss