Python
- 练习一
- 练习二
- 练习三
练习一

(回文素数)回文素数是指一个数既是素数又是回文数。例如,131 既是素数也是回文数。数字313和717都是如此。编写程序显示前 100 个回文素数。每行显示10个数字,并且准确对齐如下所示。
2 3 5 7 11 101 131 151 181 191
313 353 373 383 727 757 787 797 919 929
10301 10501 10601 11311 11411 12421 12721 12821 13331 13831
13931 14341 14741 15451 15551 16061 16361 16561 16661 17471
17971 18181 18481 19391 19891 19991 30103 30203 30403 30703
30803 31013 31513 32323 32423 33533 34543 34843 35053 35153
35353 35753 36263 36563 37273 37573 38083 38183 38783 39293
70207 70507 70607 71317 71917 72227 72727 73037 73237 73637
74047 74747 75557 76367 76667 77377 77477 77977 78487 78787
78887 79397 79697 79997 90709 91019 93139 93239 93739 94049
实现代码:
# 判断是否为素数
def is_prime(n):
if n <= 1:
return False
if n <= 3:
return True
if n % 2 == 0 or n % 3 == 0:
return False
i = 5
while (i * i <= n):
if (n % i == 0 or n % (i + 2) == 0):
return False
i += 6
return True
# 判断是否为回文数
def is_palindrome(n):
return str(n) == str(n)[::-1]
count = 0
num = 2
# 构建循环找出既是素数又是回文数的数字
while count < 100:
if is_prime(num) and is_palindrome(num):
if count % 10 == 0:
print()
print(f'{num:6}', end='')
count += 1
num += 1
首先我们定义一个函数来检查一个整数是否为素数,然后定义一个函数检查一个数字是否为回文。这之后的循环会找寻满足这两个条件的前一百个数字。每当找到一个符合条件的数字,就打印出来,然后计数加一,直到找到100个这样的数字。
结果显示:
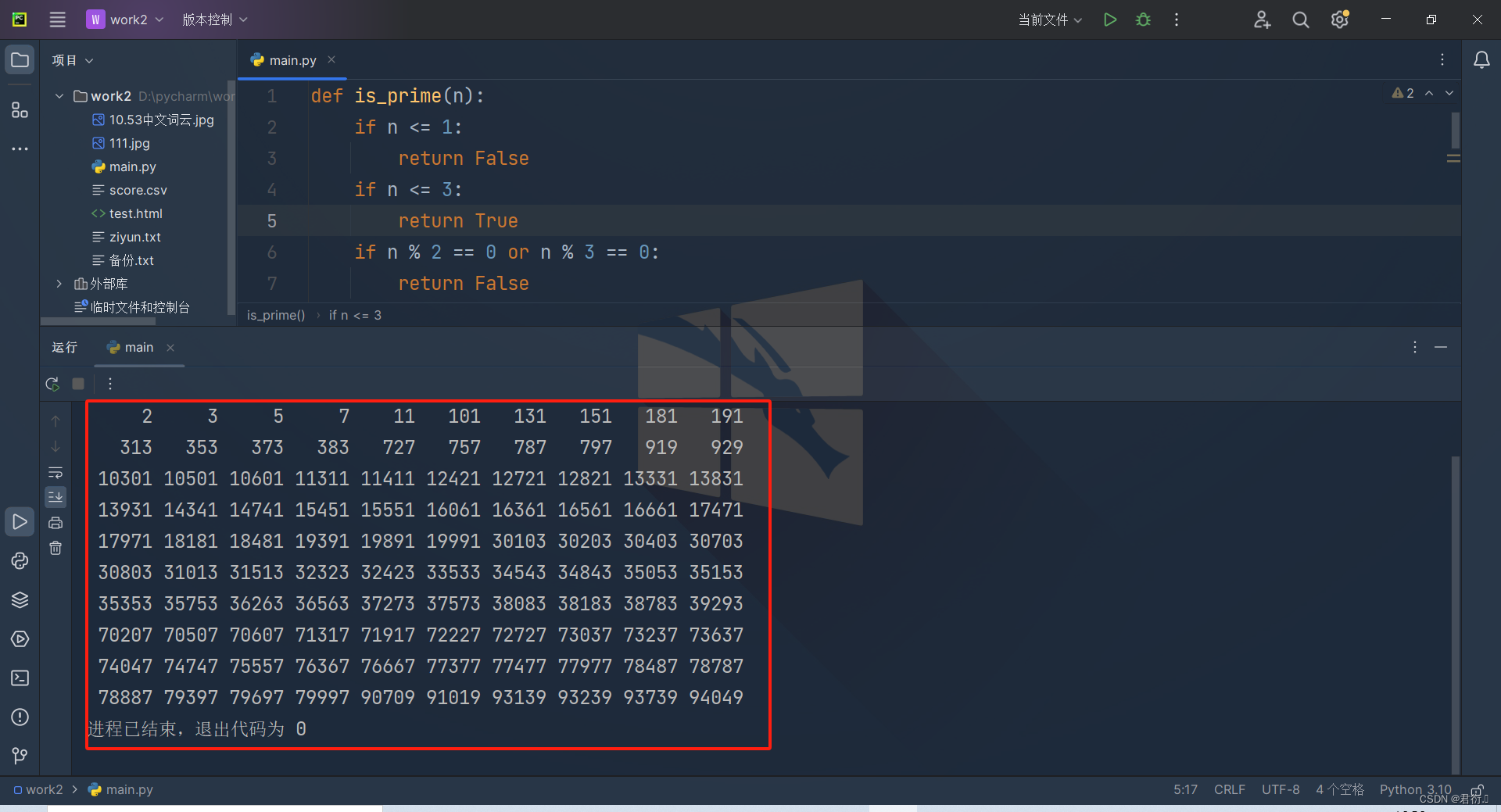
练习二

(反素数)反素数(逆向拼写的素数)是指一个将其逆向拼写后也是一个素数的非回文数。例如:17和71都是素数,所以,17和71都是反素数。编写程序显示前 100 个反素数。每行显示 10个数字,并且准确对齐,如下所示
13 17 31 37 71 73 79 97 107 113
149 157 167 179 199 311 337 347 359 389
701 709 733 739 743 751 761 769 907 937
941 953 967 971 983 991 1009 1021 1031 1033
1061 1069 1091 1097 1103 1109 1151 1153 1181 1193
1201 1213 1217 1223 1229 1231 1237 1249 1259 1279
1283 1301 1321 1381 1399 1409 1429 1439 1453 1471
1487 1499 1511 1523 1559 1583 1597 1601 1619 1657
1669 1723 1733 1741 1753 1789 1811 1831 1847 1867
1879 1901 1913 1933 1949 1979 3011 3019 3023 3049
实现代码:
# 判断是否为素数
def is_prime(n):
if n < 2:
return False
for i in range(2, int(n ** 0.5) + 1):
if n % i == 0:
return False
return True
# 判断是否为反素数
def is_emirp(n):
if n < 12:
return False
else:
return str(n) != str(n)[::-1] and is_prime(int(str(n)[::-1]))
counter = 0
n = 2
# 初始化列表来存储既是素数又是反素数
emirp_list = []
# 将既是素数又是反素数的数字进行尾增存入列表中
while counter < 100:
if is_prime(n) and is_emirp(n):
emirp_list.append(n)
counter += 1
n += 1
# 输出既是素数又是反素数的数字
for i in range(0, len(emirp_list), 10):
for j in emirp_list[i: i + 10]:
print("{:5d}".format(j), end=" ")
print()
输出结果:
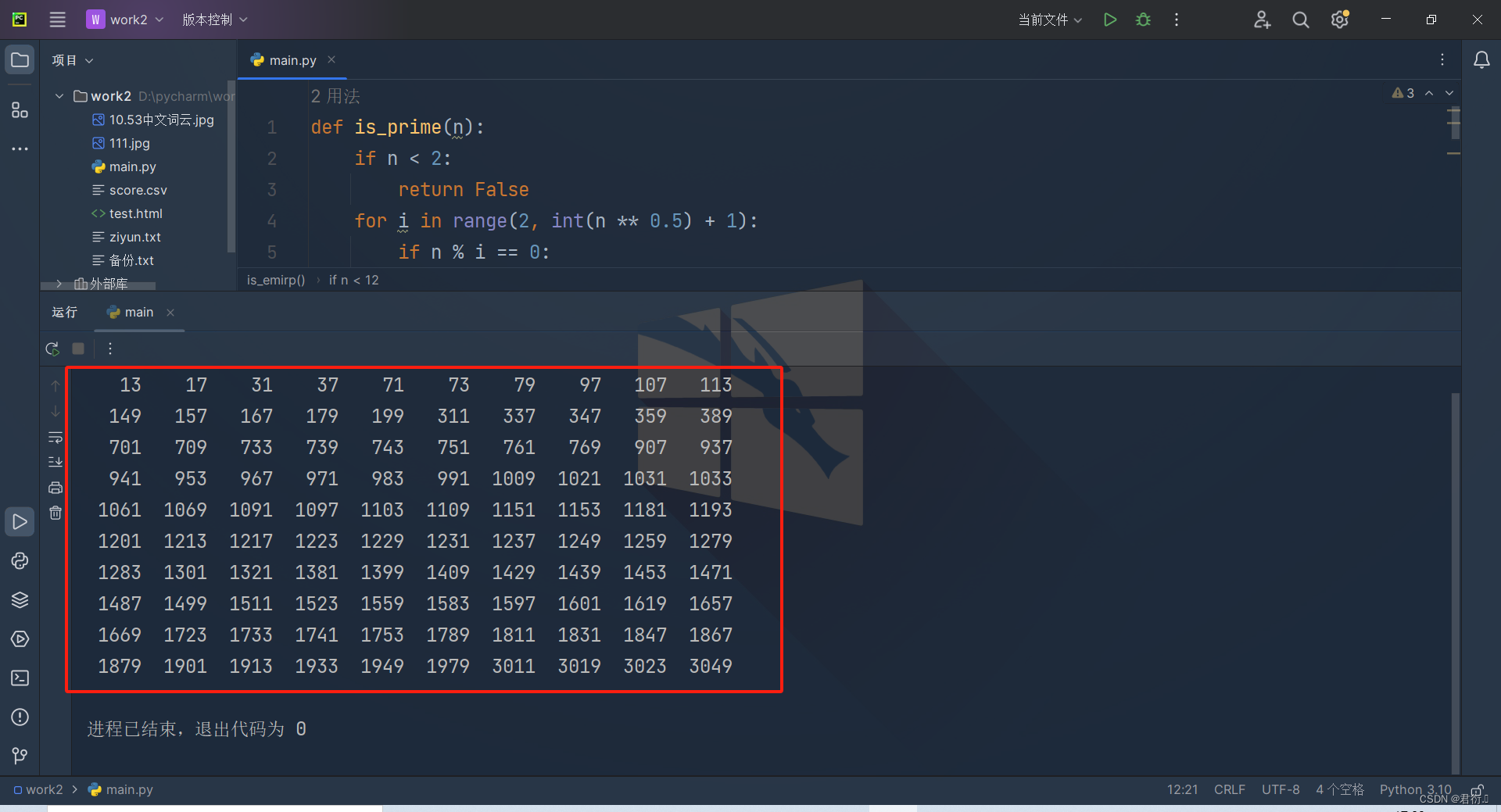
练习三

(求一个整数各个数字的和)编写一个函数,计算一个整数各个数字的和。使用下面的函数头:
def sumDigits(n):
例如:sumDigits(234)返回9(2+3+4)。(提示:使用求余运算符%提取数字,而使用除号//去掉提取出来的数字。例如:使用234%10(=4)取4然后使用234//10(=23)从234中去掉 4。使用一个循环来反复提取和去掉每个数字,直到所有数字被提取完为止。)编写程序提示用户输人一个整数,然后显示这个整数所有数字的和。
实现代码:
# 创建名为sumDigits的函数
def sumDigits(n):
# 创建列表存储整数各个位置上的数字
digits = []
while n > 0:
# 对整数进行取余存入数组
digits.append(str(n % 10))
# 对整数进行取整
n = n // 10
# 将列表数字连接起来放入字符串
sum_expression = " + " .join(reversed(digits))
# 转化为整数进行求和
sum_value = sum(map(int, digits))
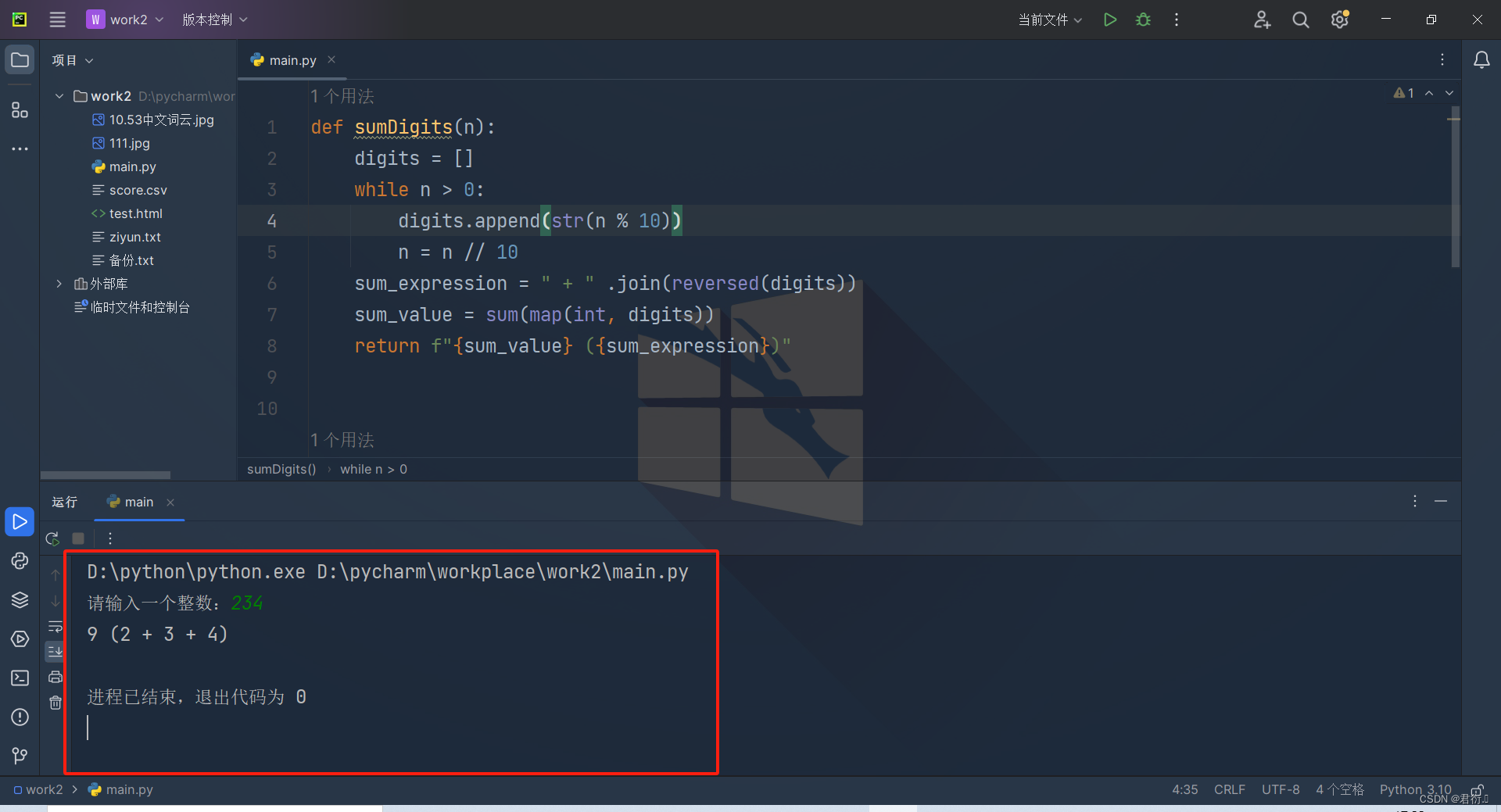
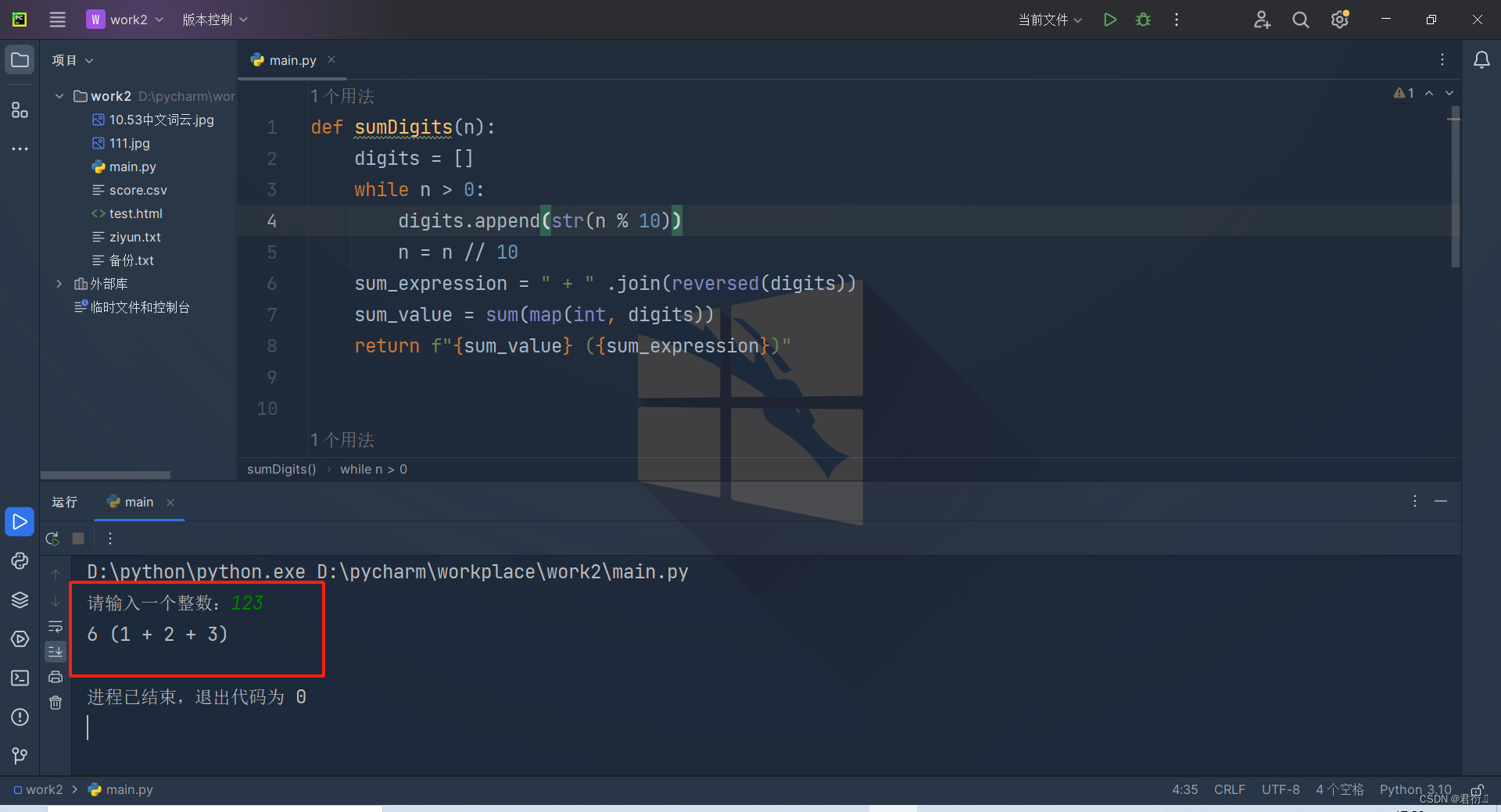
return f"{sum_value} ({sum_expression})"
def main():
number = int(input("请输入一个整数:"))
# 调用函数sumDigits
result = sumDigits(number)
print(f"{result}")
main()
输出结果: