归并排序
要将一个数组排序,可以先将它分成两半分别排序,然后再将结果合并(归并)起来。这里的分成的两半,每部分可以使用其他排序算法,也可以仍然使用归并排序(递归)。
我看《算法》这本书里对归并算法有两种实现,一种是“自顶向下”,另一种是“自底向上”。这两种方法,个人认为只是前者用了递归的方法,后者使用两个 for 循环模拟了递归压栈出栈的算法,本质上还是相同的(如果理解错误,还望大佬指出)。
算法步骤
1、将要排序的序列分成两部分。
2、将两部分分别各自排序。然后再将两个已经排序好的序列“归并”到一起,归并后的整个序列就是有序的。
3、将两个有序的序列归并的步骤:
3.1、先申请一个空间,大小足够容纳两个已经排序的序列。
3.2、设定两个指针,最初位置分别为两个已经排序序列的起始位置。
3.3、比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置。
3.4、重复3.3 步骤。
归并排序,比较重要的是“分治”思想和“归并”的操作。
归并操作,是将两个“有序”的序列,合并成一个有序的序列的方法。而这两个有序的序列,又是根据“分治”思想将一个学列分割成的两部分(将一个序列不断的分隔,到最后就剩一个的时候他自然就是有序的)。
public class MergeSort {
public static void main(String[] args) {
int[] nums = {12,123,432,23,1,3,6,3,-1,6,2,6};;
sort(nums,0,nums.length -1);
System.out.printf("finish!");
}
public static void sort(int[] nums,int left,int right){
if(left >= right){
return;
}
// 递归的将左半边排序
sort(nums,left,right - left / 2 - 1);
// 递归的将右半边排序
sort(nums,right - left / 2 ,right);
// 此时左右半边都分别各自有序,再将其归并到一起。
// 如:[1,9,10 , 3,7,8]
merge(nums,left,right - left / 2,right);
}
// 此方法叫做原地归并,将数组 nums 根据 mid 分隔开,左右看作是两个数组。
// 类似于 merge(int[] nums1,int[] nums2),将 nums1 和 nums2 归并
public static void merge(int[] nums ,int left,int mid,int right){
int i = left,j = mid;
int[] temp_nums = new int[nums.length];
for(int key = left ; key <= right; key++)
// 将原来数组复制到临时数组中。
temp_nums[key] = nums[key];
for(int key = i ; key <= right; key++){
if(i > mid){
nums[key] = temp_nums[j++];
} else if (j > right) {
nums[key] = temp_nums[i++];
} else if (temp_nums[i] > temp_nums[j]) {
nums[key] = temp_nums[j++];
}else{
nums[key] = temp_nums[i++];
}
}
}
}
快速排序
快速排序是一种分治的排序算法,它将一个数组分成两个子数组,将两部分独立的排序
快速排序可能是应用最广泛的排序算法了。快速排序流行的原因是它实现简单、适用于各种不同的输入数据且在一般应用中比其他排序算法都要快得多。——《算法(第四版)》
算法步骤
- 从数列中挑出一个元素,称为 "基准"(pivot);
- 所有元素比"基准"值小的摆放在前面,所有元素比"基准"值大的摆在后面,相同的数可以到任一边。这个称为分区(partition)操作。
- 递归地(recursive)使用同样的方法把小于基准值元素的子数列和大于基准值元素的子数列排序;
算法过程
1、给定一个乱序的数组
[5,1,4,6,2,66,34,8]
2、选择第一个为基准数,此时把第一个位置置空。两个指针,left从左到右,找比 piovt “大”的数;right 从右向左,找比 piovt “小”的数。
left right
| |
[_,1,4,6,2,66,34,8]
|
piovt = 5
3、right 从右向左(<-),找比 piovt “小”的数 2。
left right
| |
[_,1,4,6,2,66,34,8]
|
piovt = 5
4、left从左到右(->),找到了比 piovt 大的数 6。
left right
| |
[_,1,4,6,2,66,34,8]
|
piovt = 5
5、此时将 left 和 right 上的数对调。
left right
| |
[_,1,4,2,6,66,34,8]
|
piovt = 5
6、right 继续向左查找,直到 left = right。(正常情况下要重复 4、5 步骤多次才会得到 left = right)
此时将 left 位置的数放到原来 piovt 位置上,将 piovt 放到 left 位置上。
left
right
|
[2,1,4,5,6,66,34,8]
- -
|
piovt = 5
7、此时将整个数组根据 piovt 分割成两个部分,左边都比 piovt 小,右边都比 piovt 大。递归的处理左右两部分。
实现
public class QuickSort {
public static void main(String[] args) {
int[] nums = {5,1,4,6,2,66,34,8,34,534,5};
int[] sorted = sort(nums,0 , nums.length - 1);
System.out.println("finish!");
}
// 排序
public static int[] sort(int[] nums , int left , int right){
if(left <= right){
// 将 nums 以 mid 分成两部分
// 左边的小于 nums[min]
// 右边的大于 nums[min]
int mid = partition(nums,left,right);
// 递归
sort(nums,left,mid - 1);
sort(nums,mid + 1 ,right);
}
return nums;
}
public static int partition(int[] nums , int left , int right){
//int pivot = left;
int i = left , j = right + 1; // 左右两个指针
int pivot = nums[left]; // 基准数,比他小的放到左边,比他大的放到右边。
while ( true ){
// 从右向左找比 pivot 小的。
while (j > left && nums[--j] > pivot){
if(j == left){
// 到头了
break;
}
}
// 先从左向右找比 pivot 大的。
while (i < right && nums[ ++ i] < pivot ){
if( i == right){
// 到头了
break;
}
}
if(i >= j ) break;
// 交换 i 位置和 j 位置上的数
// 因为此时 nums[i] > pivot 并且 nums[j] < pivot
swap(nums,i , j);
}
// 由于 left 位置上的数是 pivot=
// 此时 i = j 且 nums[i/j] 左边的数都小于 pivot , nums[i/j] 右边的数都大于 pivot。
// 此时交换 left 和 j 位置上的数就是将 pivot 放到中间
swap(nums,left,j);
return j ;
}
// 交换数组中两个位置上的数
public static void swap(int[] nums , int i1 , int i2){
int n = nums[i1];
nums[i1] = nums[i2];
nums[i2] = n;
}
}
堆排序
堆排序主要是利用“堆”这种数据结构的特性来进行排序,它本质上类似于“选择排序”。都是每次将最大值(或最小值),找出来放到数列尾部。不过“选择排序”需要遍历整个数列后选出最大值(可以到上面再熟悉下选择排序算法),“堆排序”是依靠堆这种数据结构来选出最大值。但是每次重新构建最大堆用时要比遍历整个数列要快得多。
堆排序中用到的两种堆,大顶堆和小顶堆:
1、大顶堆:每个节点的值都大于或等于其子节点的值(在堆排序算法中一般用于升序排列);
2、小顶堆:每个节点的值都小于或等于其子节点的值(在堆排序算法中一般用于降序排列);
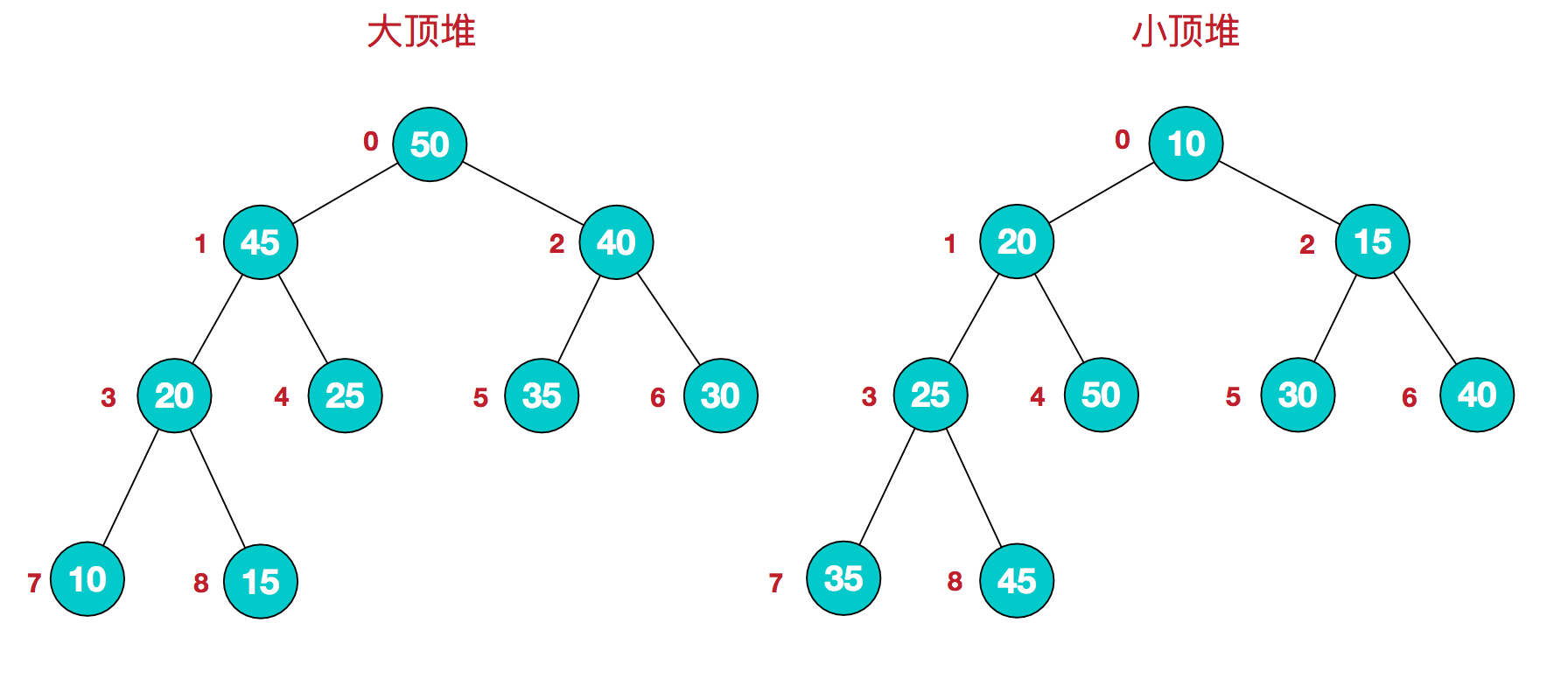
我们给树的每个节点编号,并将编号映射到数组的下标就是这样:

该数组从逻辑上是一个堆结构,我们用公式来描述一下堆的定义就是:
1、大顶堆:arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2]
2、小顶堆:arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]
这里只要求父节点大于两个子节点,并没有要求左右两个子节点的大小关系。
算法过程
1、将一个 n 长的待排序序列arr = [0,……,n-1]构造成一个大顶堆。
2、此时数组的 0 位置(也就是堆顶),就是数组的最大值了,将其与数组的最后一个数交换。
3、将剩下 n-1 个数重复 1和2 操作,最终会得到一个有序的序列。
堆排序是“选择排序”的一种变体,算法中比较难的地方是用数组构建“大顶堆”或“小顶堆”的过程。
实现堆排序前,我们要知道怎么用数组构建一个逻辑上的最大堆,这里会用到几个公式(假设当前节点的序号是 i,可以结合上图理解下下面的公式):
1、左子节点的序号就是:2i + 1;
2、右子几点的序号就是:2i + 2;
3、父节点的序号就是:(i-1) / 2 (i不为0);
public class HeapSort {
static int temp ;
public static void main(String[] args) {
int[] nums = {5,1,4,6,2,66,-1,34,-9,8};
sort(nums);
System.out.println("finish!");
}
public static void sort(int[] nums){
// 第一步要先将 nums 构建成最大堆。
for(int i = (nums.length - 1) / 2 ; i >= 0; i-- ){
//从第一个非叶子结点从下至上,从右至左调整结构
maxHeapify(nums,i,nums.length);
}
// 遍历数组
// j 是需要排序的数组的最后一个索引位置。
for(int j = nums.length - 1 ; j > 0 ; j --){
// 每次都调整最大堆堆顶(nums[0]),与数组尾的数据位置(nums[j])。
swap(nums,0,j);
// 重新调整最大堆
maxHeapify(nums,0,j);
}
}
/**
* 将 nums 从 i 开始的 len 长度调整成最大堆。
* (注意:此方法只适合调整已经是最大堆但是被修改了的堆,或者只有三个节点的堆)
* len :需要计算到数组 nums 的多长的地方。
* i :父节点在的位置。
*/
public static void maxHeapify(int[] nums,int i , int len){
// 是从左子节点开始
int key = 2 * i + 1;
if(key >= len){
// 说明没有子节点。
return;
}
// key + 1 是右子节点的位置。
if(key + 1 < len && nums[key] < nums[key + 1]){
// 此时说明右节点比左节点大。
// 此时只要将父节点跟 右子节 点比就行了。
key += 1;
}
if(nums[i] < nums[key]){
// 子节点比父节点大,交换子父界节点的数据,将父节点设置为最大。
swap(nums,i,key);
// 此时子节点上的数变了,就要递归的再去,计算子节点是不是最大堆。
maxHeapify(nums,key,len);
}
}
/**
* 交换 i 和 j 位置的数据
*/
public static void swap(int[] nums,int i,int j){
temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
}