前言

本文将会向你介绍什么是快速选择算法，（用两道例题来讲解）算法原理是什么

引入

快速选择算法和快速排序算法都是基于分治思想的算法，它们的基本原理是类似的，都是通过将数组分成两部分，然后递归地处理这两部分。

快速选择算法和快速排序算法的主要区别在于它们的应用场景和目的。

快速排序算法的目的是对整个数组进行排序，它会通过递归的方式不断地将数组分成两部分，直到整个数组有序为止。

快速选择算法的目的是在无序数组中查找第k小（或第k大）的元素，它不需要对整个数组进行排序，而是通过类似快速排序的分区操作，只处理包含目标元素的那一部分数组，从而减少了不必要的操作。
这种方法能够在平均情况下达到O(n)的时间复杂度，因此被广泛应用于求解第k小（或第k大）元素的问题

颜色分类

戳这 -> 颜色分类

类⽐数组分两块的算法思想，这⾥是将数组分成三块，那么我们可以再添加⼀个指针，实现数组分三块。
设数组⼤⼩为 n ，定义三个指针 left, i, right :

left ：⽤来标记 0 序列的末尾，因此初始化为 -1 ； ◦ cur ：⽤来扫描数组，初始化为 0 ；
right ：⽤来标记 2 序列的起始位置，因此初始化为 n 。
在 cur 往后扫描的过程中，保证：
[0, left] 内的元素都是 0 ；
[left + 1, i - 1] 内的元素都是 1 ；
[i, right - 1] 内的元素是待定元素；
[right, n] 内的元素都是 2 。

class Solution {
public:
    void sortColors(vector<int>& nums) 
    {
        int n = nums.size();
        //i:遍历区间，left：标记0区域最右侧，right：标记2区域最左侧
        // 0：[0,left]
        // 1：[left+1, i-1]
        // 待扫描区域：[i, right-1]
        // 2：[right, n-1]
        int left = -1, right = n, i = 0; 
        while(i < right)
        {
            if(nums[i] == 0)
            {
                std::swap(nums[++left], nums[i++]);
            }
            else if(nums[i] == 1)
            {
                i++;
            }
            else if(nums[i] == 2)
            {
                //i不能++，交换完后，还得判断交换后这个值是多少
                std::swap(nums[--right], nums[i]);
            }
        }
    }
};

数组中第k个最大的数

注意：要求实现时间复杂度欸O(n)的算法

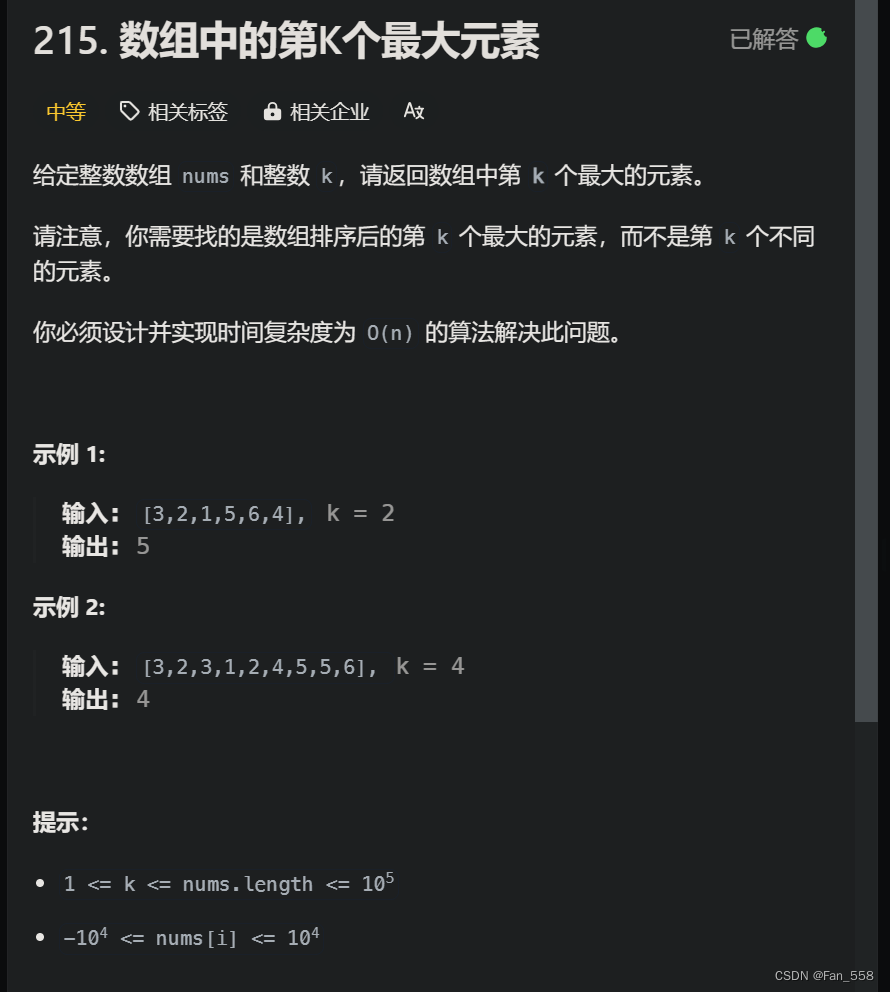
利用颜色分类中数组分三块的思想+随机选择基准值来决定在哪一块区间中查找

戳这->数组中第k个最大的数

class Solution {
public:
    int findKthLargest(vector<int>& nums, int k) 
    {
        //种下随机数种子
        srand(time(nullptr));
        return qsort(nums, 0, nums.size()-1, k);
    }

    int getRandom(vector<int>& nums, int left,int right)
    {
        //rand() % (right - left + 1)生成一个随机数范围为[0, right-left]的值，+left生成一个随机数范围为[left, right-left]
        return nums[rand() % (right - left + 1) + left];
    }

    int qsort(vector<int>& nums, int l, int r, int k)
    {
        //获得随机值
        int key = getRandom(nums, l, r);
        int left = l - 1, right = r + 1, i = l;
        //当区间只有一个元素
        if(l==r)
        {
            return nums[l];
        }
        //划分三组区间
        while(i < right)
        {
            if(nums[i] > key)
            {
                swap(nums[i], nums[--right]);
            }
            else if(nums[i] == key)
            {
                i++;
            }
            else if(nums[i] < key)
            {
                swap(nums[i++], nums[++left]);
            }
        }
        //<key      =key                >key
        //[l,left], [left+1, right-1], [right, r]
        int b = right - left - 1, c = r - right + 1;
        //（本质是缩小区间）
        //第k大的元素，在[right, r]区间中（再此区间中查找）
        if(c >= k) 
        {
            return qsort(nums, right, r, k);
        }
        //进入此条件，说明第k大的元素不在[right,r]中，在[left+1, right-1]中，而此区间的元素就是key直接返回即可
        else if(b + c >= k)
        {
            return key;
        }
        //进入此条件，第k大的元素在[l,left]中（在此区间中查找）
        else 
        {
            return qsort(nums, l, left, k - b - c);
        }
    }
};

以下是分治的思想，将数组分成三块，缩小查找范围（递归调用去找）

   <key      =key                >key
 [l,left], [left+1, right-1], [right, r]

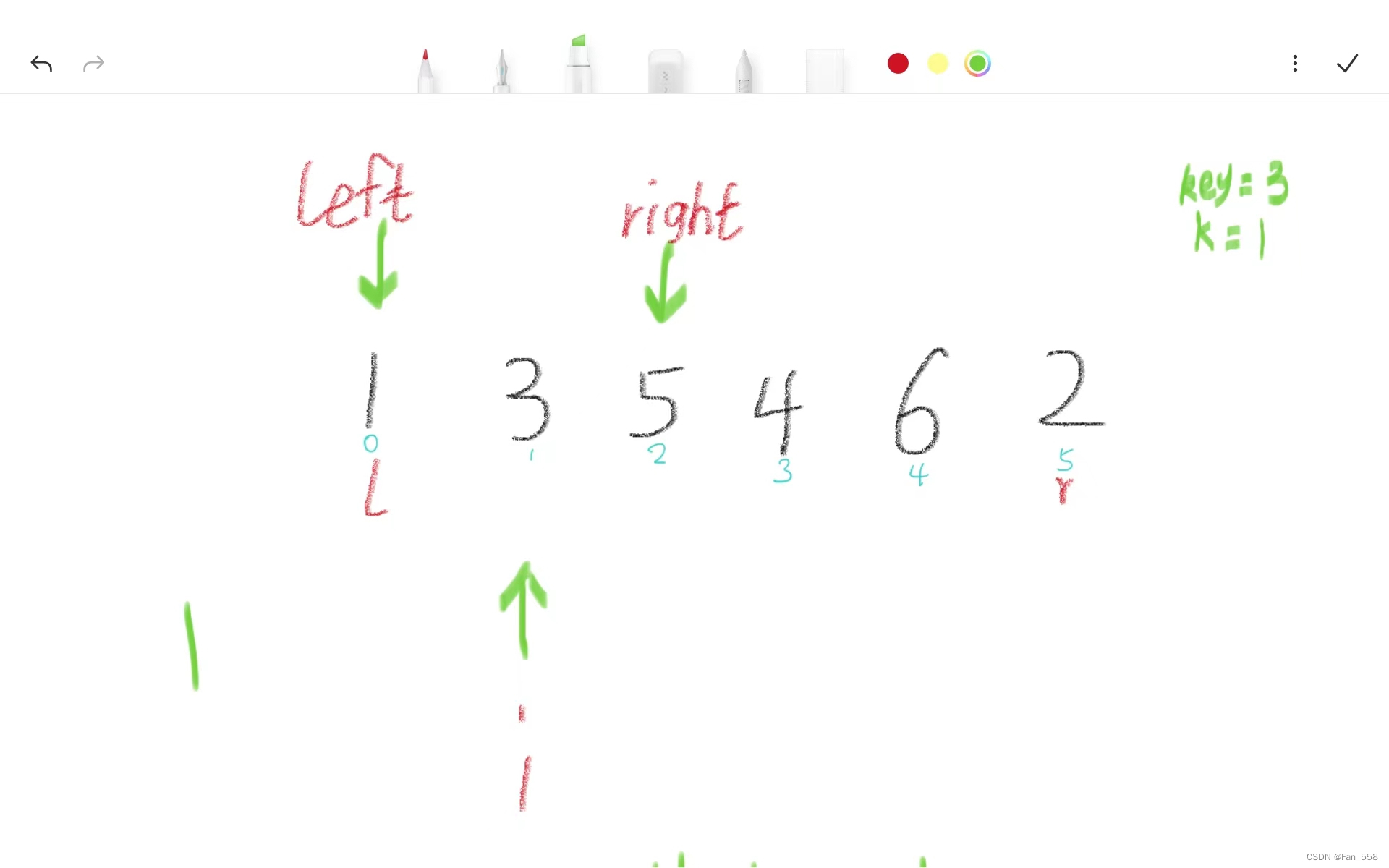
此时再将新的l与r作为参数传入调用

当然随机数的选取的区间也变成了新的[l, r],剩余的操作就不一一演示了，大家可以自己去模拟这个过程

这里的k都只是假设出来的，当k=1时，此时c>=1, 需要到[right, r]区间中寻找最大第k个元素

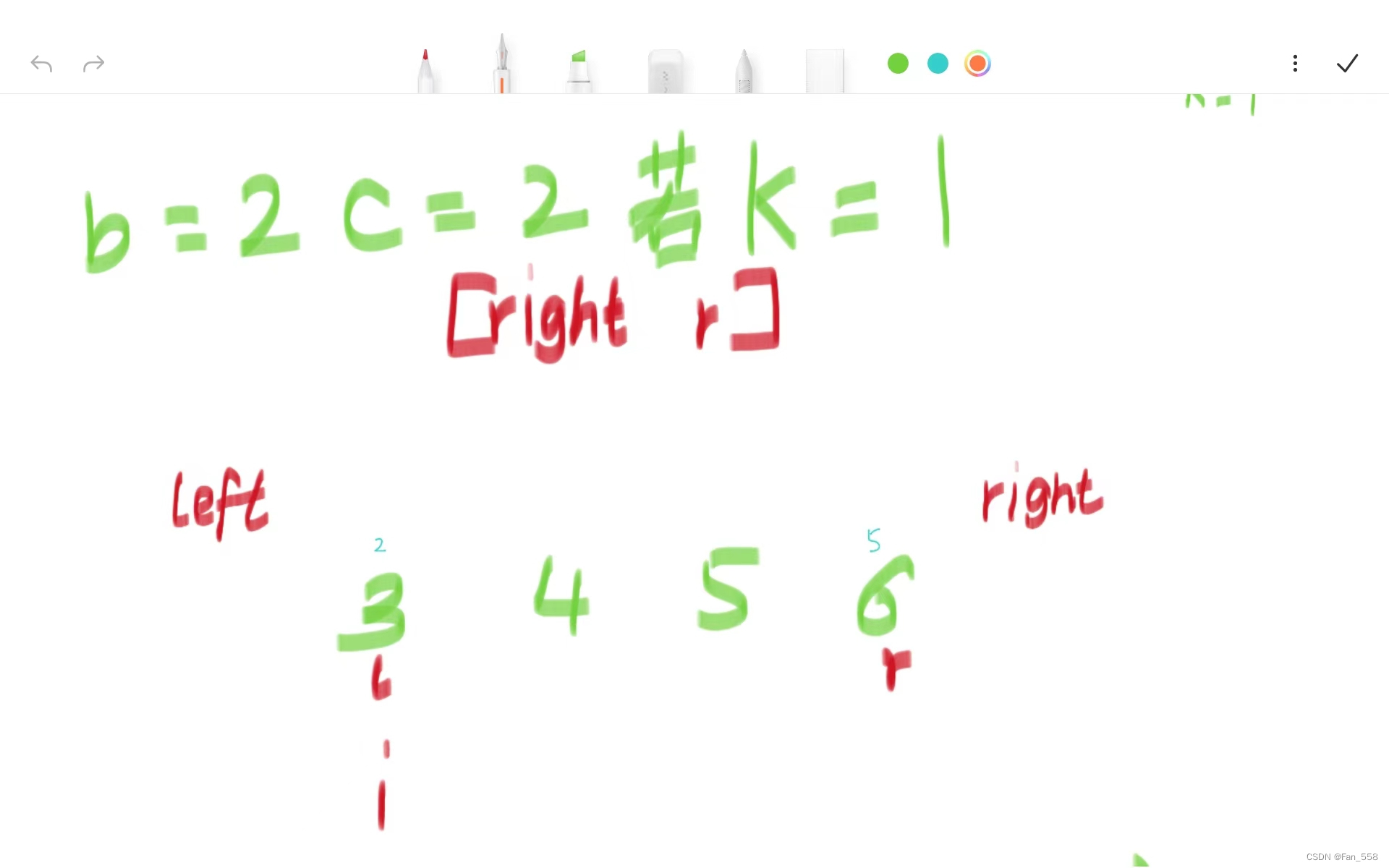
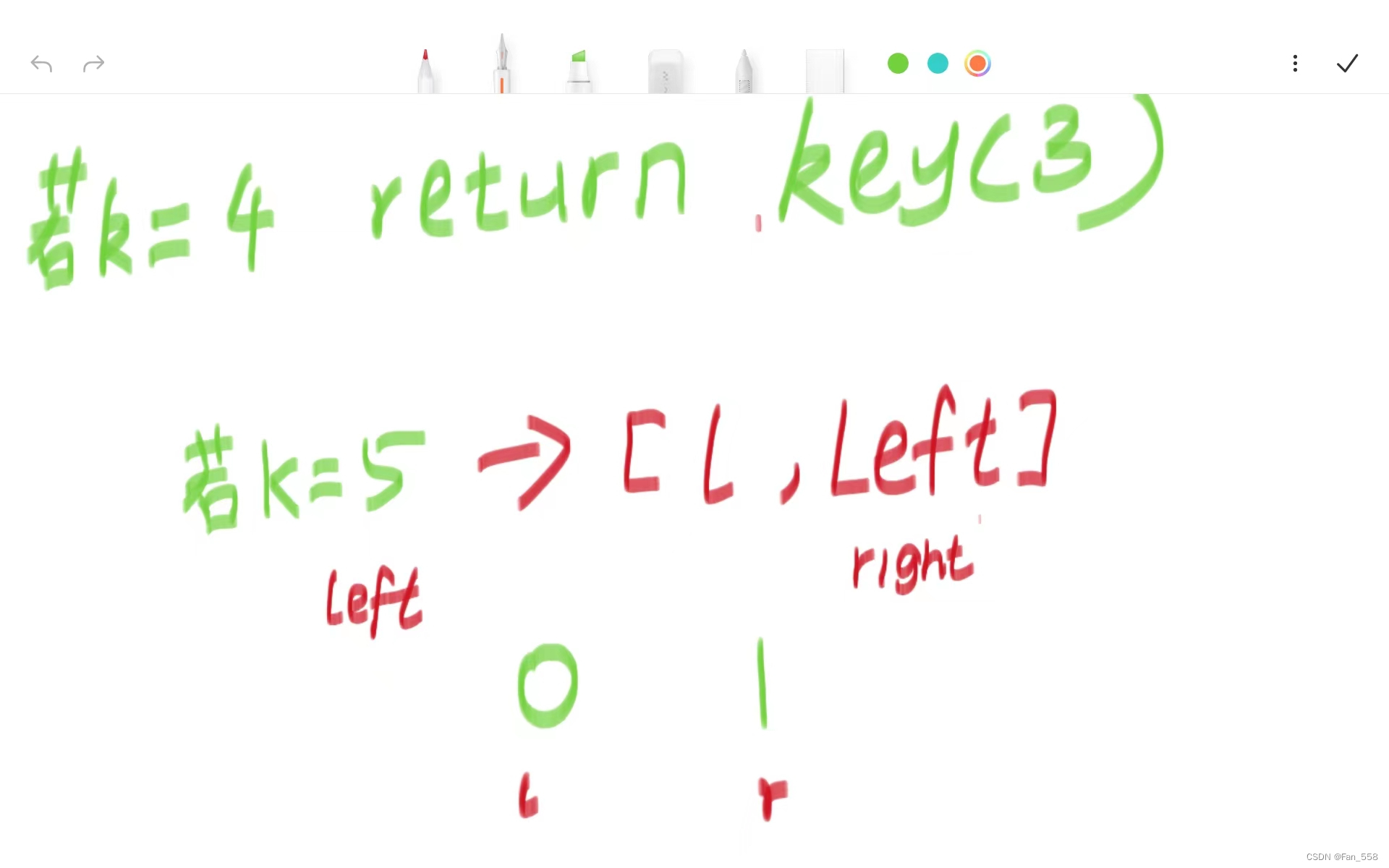
当k=4的时候（此时运气比较好，key刚好就是第四大的数，直接返回即可） 当k=5的时候，此时b+c < k，进入[l, left]区间中寻找第(k-b-c)个数

其它例题

戳这->最小的k个数
戳这->排序数组

小结

今日的分享就到这里啦，后续会持续更新其他的算法讲解，如果本文存在疏忽或错误的地方还请您能够指出！