文章目录
- 11. 二叉树的层序遍历
- 题目描述
- 代码与解题思路
- 12. 搜索旋转排序数组
- 题目描述
- 代码与解题思路
- 13. 买卖股票的最佳时机
- 题目描述
- 代码和解题思路
- 14. 岛屿数量
- 题目描述
- 代码与解题思路
- 15. 环形链表
- 题目描述
- 代码与解题思路
- 16. 有效的括号
- 题目描述
- 代码与解题思路
- 17. 合并两个有序数组
- 题目描述
- 代码与解题思路
- 18. 全排列
- 题目描述
- 代码与解题思路
- 19. 二叉树的最近公共祖先
- 题目描述
- 代码与解题思路
- 20. 二叉树的锯齿形层序遍历
- 题目描述
- 代码与解题思路
11. 二叉树的层序遍历
题目链接:102. 二叉树的层序遍历
题目描述
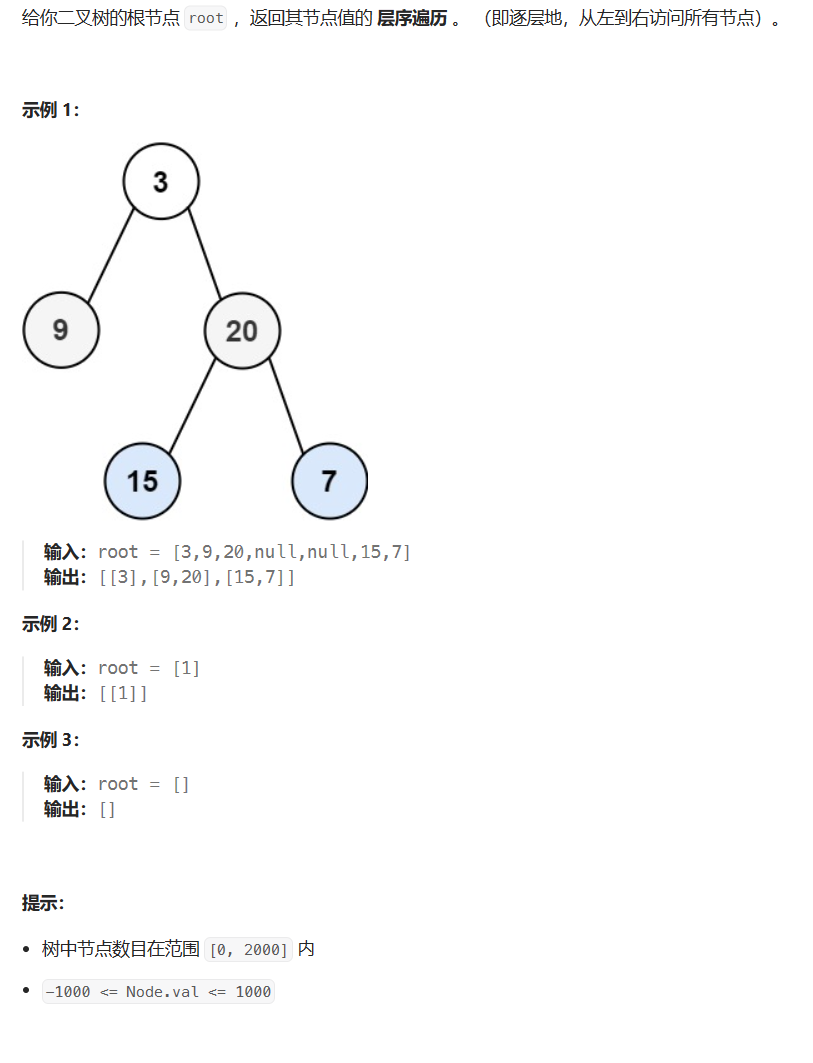
代码与解题思路
/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func levelOrder(root *TreeNode) (ans [][]int) {
if root == nil {
return
}
curQueue := []*TreeNode{root}
for len(curQueue) > 0 {
nextQueue := curQueue
curQueue = nil
tmp := []int{}
for _, v := range nextQueue {
tmp = append(tmp, v.Val)
if v.Left != nil {
curQueue = append(curQueue, v.Left)
}
if v.Right != nil {
curQueue = append(curQueue, v.Right)
}
}
ans = append(ans, tmp)
}
return ans
}
多练习就行,把层序遍历的模板背下来
12. 搜索旋转排序数组
题目链接:33. 搜索旋转排序数组
题目描述

代码与解题思路
func search(nums []int, target int) int {
left, right := 0, len(nums)-1
for left <= right {
mid := left+(right-left)/2
if nums[mid] == target {
return mid
}
if nums[mid] >= nums[left] { // mid 在左区间
if target >= nums[left] && target < nums[mid] { // target 在 mid 左边
right = mid-1
} else { // target 在 mid 右边
left = mid+1
}
} else { // mid 在右区间
if target <= nums[right] && target > nums[mid] { // target 在 mid 右边
left = mid+1
} else { // target 在 mid 左边
right = mid-1
}
}
}
return -1
}
二分还是得靠多练多思考,这里的情况很多,如果再遇到类似的情况,冷静分析,一点点的用 if else 就行,不用畏手畏脚的。
13. 买卖股票的最佳时机
题目链接:121. 买卖股票的最佳时机
题目描述

代码和解题思路
func maxProfit(prices []int) int {
minPrice, profit := 10000, 0
for _, v := range prices {
minPrice = min(minPrice, v)
profit = max(profit, v-minPrice)
}
return profit
}
核心思路:minPrice 记录历史最低价格,profit 记录往后的每次最高价格卖出赚到的钱,这样遍历完一次就能得到最大的利润了。
14. 岛屿数量
题目链接:200. 岛屿数量
题目描述

代码与解题思路
func numIslands(grid [][]byte) (cnt int) {
for i := 0; i < len(grid); i++ {
for j := 0; j < len(grid[0]); j++ {
if grid[i][j] == '1' {
dfs(grid, i, j)
cnt++
}
}
}
return cnt
}
func dfs(grid [][]byte, i, j int) {
if i < 0 || j < 0 || i >= len(grid) || j >= len(grid[0]) || grid[i][j] == '0' {
return
}
grid[i][j] = '0'
dfs(grid, i+1, j)
dfs(grid, i-1, j)
dfs(grid, i, j+1)
dfs(grid, i, j-1)
}
这是一道基础的 dfs 题目,代码的核心点有三个部分:
- 遍历整个二维数组进行 dfs
- 只搜索:上下左右
- 将搜索过的位置置为 ‘0’
其实就是基础的 dfs 需要注意的点,然后注意一下边界条件就行。
15. 环形链表
题目链接:141. 环形链表
题目描述
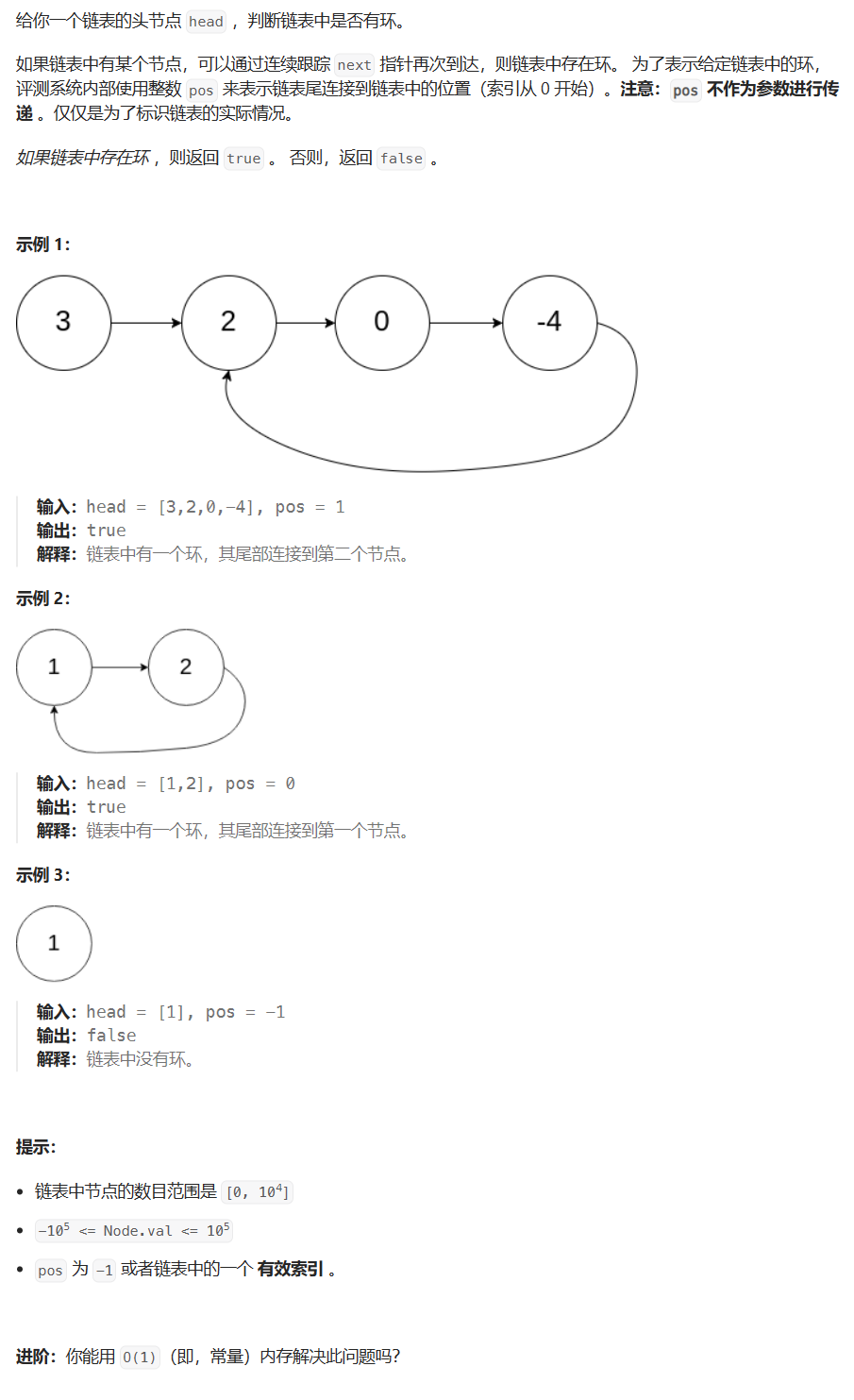
代码与解题思路
/**
* Definition for singly-linked list.
* type ListNode struct {
* Val int
* Next *ListNode
* }
*/
func hasCycle(head *ListNode) bool {
if head == nil || head.Next == nil {
return false
}
pre, cur := head, head
for cur.Next != nil && cur.Next.Next != nil {
pre = pre.Next
cur = cur.Next.Next
if pre == cur {
return true
}
}
return false
}
这道题目实际上是可以用哈希来做的,我们遍历放进哈希表,当遇到相同节点的时候就证明链表有环了,如果没遇到就证明没有,就用 head != nil 来做结束条件,有尾就结束了,有环就会再进一次哈希。
不过我这段代码用的是更优的方法,用的是追击算法,慢指针一次一步,快指针一次两步,最后一定能够追上。面试的时候可以把上面的思路讲一讲,然后实现下面这种解法。
16. 有效的括号
题目链接:20. 有效的括号
题目描述

代码与解题思路
func isValid(s string) bool {
hash := map[byte]byte{')':'(', '}':'{', ']':'['}
stack := []byte{}
for i := 0; i < len(s); i++ {
if s[i] == '(' || s[i] == '[' || s[i] == '{' {
stack = append(stack, s[i])
} else if len(stack) > 0 && stack[len(stack)-1] == hash[s[i]] {
stack = stack[:len(stack)-1]
} else {
return false
}
}
return len(stack) == 0
}
这道题目最重要的就是分析好可能出现的情况:
第一种情况:已经遍历完了字符串,但是栈不为空,说明有相应的左括号没有右括号来匹配,所以 return false;
第二种情况:遍历字符串匹配的过程中,发现栈里没有要匹配的字符,所以return false;
第三种情况:遍历字符串匹配的过程中,栈已经为空了,没有匹配的字符了,说明右括号没有找到对应的左括号 return false;
字符串遍历完之后,栈是空的,就说明全都匹配了。
分析完之后,直接根据需求写代码就行了。
小技巧:通过 map 映射少写几个 if else 语句。
17. 合并两个有序数组
题目链接:88. 合并两个有序数组
题目描述

代码与解题思路
func merge(nums1 []int, m int, nums2 []int, n int) {
tmp := []int{}
i, j := 0, 0
for m > 0 && n > 0 {
if nums1[i] < nums2[j] {
tmp = append(tmp, nums1[i])
i++
m--
} else {
tmp = append(tmp, nums2[j])
j++
n--
}
}
for m > 0 {
tmp = append(tmp, nums1[i])
i++
m--
}
for n > 0 {
tmp = append(tmp, nums2[j])
j++
n--
}
for i := 0; i < len(nums1); i++ {
nums1[i] = tmp[i]
}
}
首先是我的朴素解法,开一个 tmp 数组合并好了,然后再赋值给 nums1 数组,这样空间复杂度是 O(N),但也是最容易想的一种方法
如果想要原地进行合并的话,就需要用到题目给我们准备的 nums[] 数组给出的后面补的 0 的空间,然后从后往前合并(主要得记住从后往前遍历而不会造成覆盖的思想)
func merge(nums1 []int, m int, nums2 []int, n int) {
p1, p2, p := m-1, n-1, m+n-1
for p2 >= 0 { // 从后往前遍历
if p1 >= 0 && nums1[p1] > nums2[p2] {
nums1[p] = nums1[p1]
p1--
} else {
nums1[p] = nums2[p2]
p2--
}
p--
}
}
18. 全排列
题目链接:46. 全排列
题目描述

代码与解题思路
func permute(nums []int) (ans [][]int) {
n := len(nums)
path := make([]int, n)
onPath := make([]bool, n)
var dfs func(i int)
dfs = func(i int) {
if i == n {
// 这个方式创建了一个新的切片,保证了 path 切片和新切片不共享内存
ans = append(ans, append([]int(nil), path...))
return
}
for j, on := range onPath { // 每次进入都会枚举所有数,所有情况都会走一遍
if on == false {
path[i] = nums[j]
onPath[j] = true
dfs(i+1)
onPath[j] = false
}
}
}
dfs(0)
return ans
}
注释很明了了,注意 go 的二维数组追加切片的方式就行,dfs 的模板算法,忘了就多练,多练几次就记住了。
19. 二叉树的最近公共祖先
题目链接:236. 二叉树的最近公共祖先
题目描述
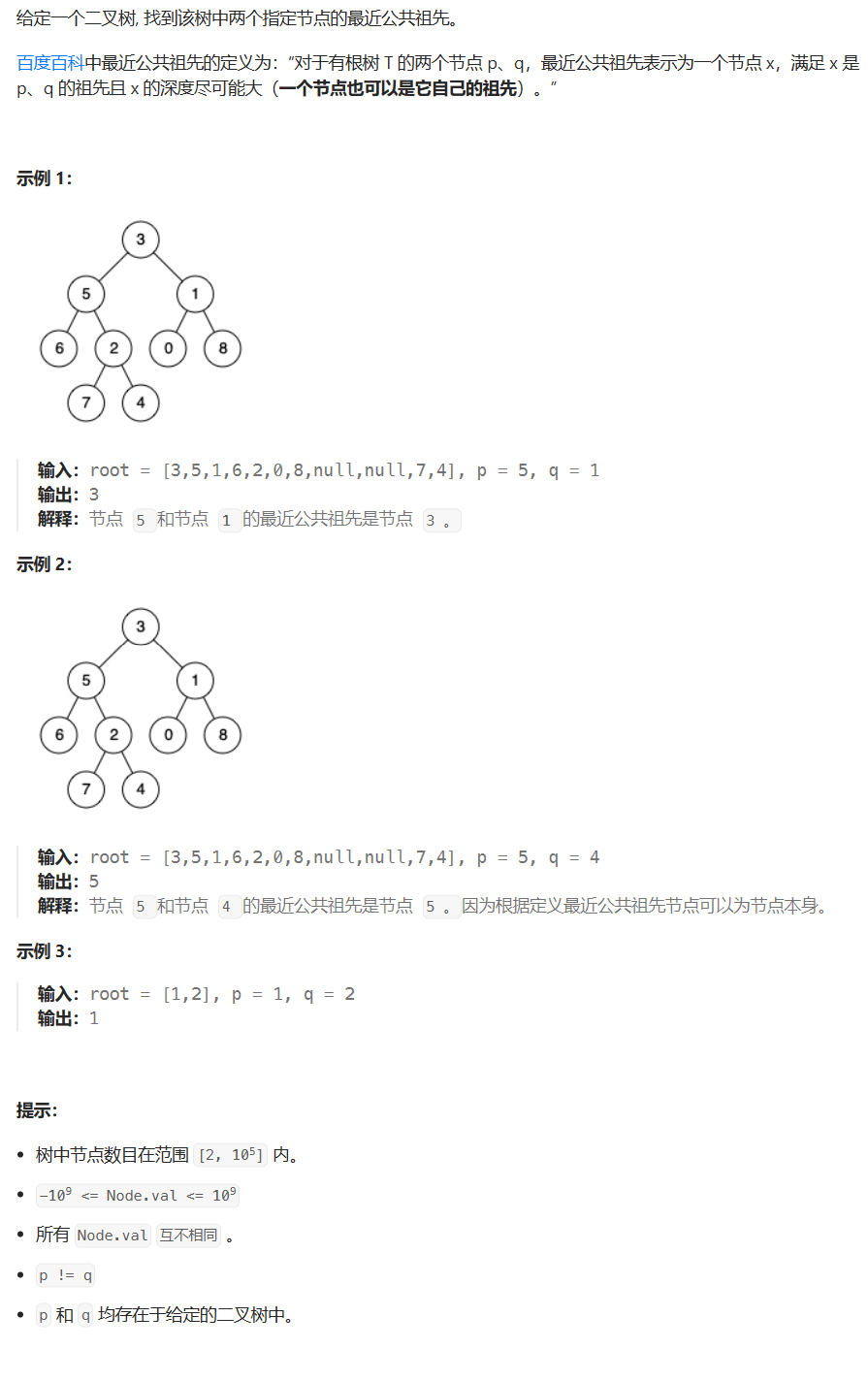
代码与解题思路
/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func lowestCommonAncestor(root, p, q *TreeNode) *TreeNode {
// 走到空节点或者找到了, 就返回
if root == nil || root == p || root == q {
return root
}
// 左右找 p 和 q
left := lowestCommonAncestor(root.Left, p, q)
right := lowestCommonAncestor(root.Right, p, q)
// 如果左右都找不到 p 和 q, 就就返回空
if left == nil && right == nil {
return nil
}
// 左子树找不到, 就返回右子树找的结果
if left == nil {
return right
}
// 右子树找不到, 就返回左子树找的结果
if right == nil {
return left
}
// 左右子树都找到了 p 或 q, 那 root 就是他们最近的公共祖先
return root
}
这道题不好想,多刷几遍,把这个思路背下来,然后一直用这一个思路来做题就行,这个思路还是非常的清晰的,刷熟了应该没有问题,注释非常的详细。需要注意的是:前三行代码已经把整个树搜索过一遍了,能走到后面的代码证明 left 和 right 的值已经出来了。
20. 二叉树的锯齿形层序遍历
题目链接:103. 二叉树的锯齿形层序遍历
题目描述
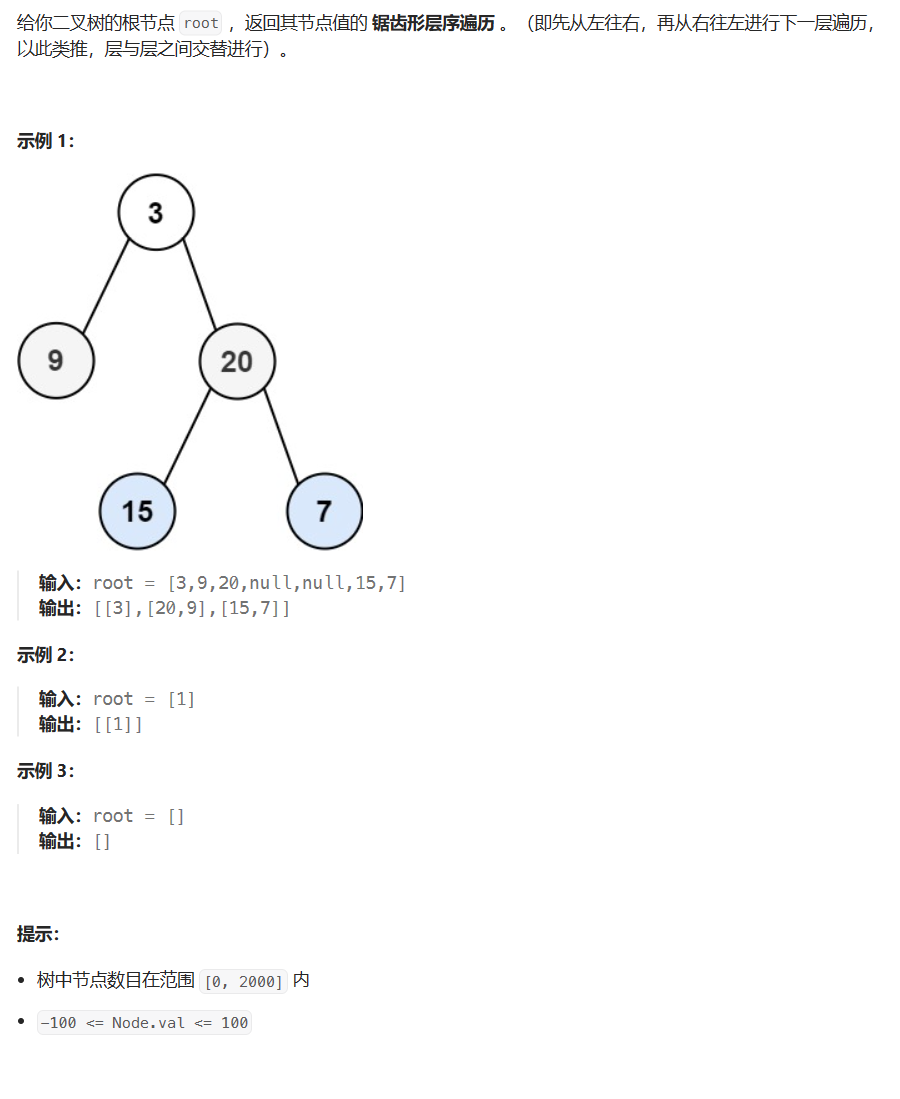
代码与解题思路
/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func zigzagLevelOrder(root *TreeNode) (ans [][]int) {
if root == nil {
return
}
q := []*TreeNode{root}
n := 0
for len(q) > 0 {
nextq := []*TreeNode{}
tmp := make([]int, len(q))
for i, v := range q {
if n%2 == 0 {
tmp[i] = v.Val
} else {
tmp[len(q)-1-i] = v.Val
}
if v.Left != nil {
nextq = append(nextq, v.Left)
}
if v.Right != nil {
nextq = append(nextq, v.Right)
}
}
n++
q = nextq
ans = append(ans, tmp)
}
return ans
}
依旧是熟悉的配方,熟悉的层序遍历,还是得多刷几遍层序遍历的模板,不然总是记不住,主要就是添加了 n 这个变量来判断要不要反着插入数据,其他的地方就是层序遍历(需要注意的地方:通过创建一个足够大小的数组,然后根据下标来完成正序和倒序的插入,学习一下这个思路)