目录
第一步、Laravel 一般使用 composer安装
第二步、使用composer安装项目
第三步、配置环境
第四步、访问域名,安装完成
Laravel 官网
lInstallation - Laravel 中文网 为 Web 工匠创造的 PHP 框架
第一步、Laravel 一般使用 composer安装
如果没有安装,安装方法如下
windows安装composer并更换国内镜像_composer切换镜像-CSDN博客
第二步、使用composer安装项目
打开cmd窗口,进入放置项目

输入
composer create-project laravel/laravel example安装完成如下

第三步、配置环境
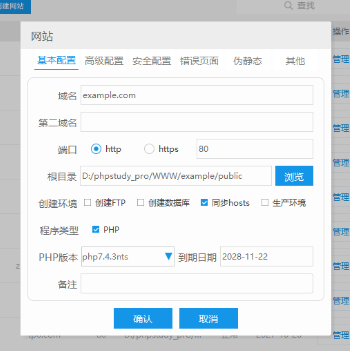
设置伪静态

<IfModule mod_rewrite.c>
Options +FollowSymlinks -Multiviews
RewriteEngine On
RewriteCond %{REQUEST_FILENAME} !-d
RewriteCond %{REQUEST_FILENAME} !-f
RewriteRule ^(.*)$ index.php [L,E=PATH_INFO:$1]
</IfModule>
第四步、访问域名,安装完成