1 Debugging programs using gdb
1.1 gdb简介
gdb是一个功能强大的调试工具,可以用来调试C程序或C++程序。在使用这个工具进行程序调试时,主要涉及下面几个方面的操作:
- 启动程序:在启动程序时,可以设置程序运行环境。
- 设置断点:程序会在断点处停止,以便于用户 查看程序的运行情况。
- 查看信息:在断点停止后,可以查看程序的运行信息和显示程序变量的值。
- 分步运行:可以让程序一个语句一个语句地执行,这时可以及时查看程序的信息。
- 改变环境:可以在程序运行时改变程序的运行环境和程序变量。
1.2 gdb常用指令
- list/l 行号:显示binFile源代码,接着上次的位置往下列,每次列10行。
- list/l 函数名:列出某个函数的源代码。
- r或run:运行程序。
- n 或 next:单条执行。
- s或step:进入函数调用
- break(b) 行号:在某一行设置断点
- break 函数名:在某个函数开头设置断点
- info break :查看断点信息。
- finish:执行到当前函数返回,然后挺下来等待命令
- print(p):打印表达式的值,通过表达式可以修改变量的值或者调用函数
- p 变量:打印变量值。
- set var:修改变量的值
- continue(或c):从当前位置开始连续而非单步执行程序
- run(或r):从开始连续而非单步执行程序
- delete breakpoints:删除所有断点
- delete breakpoints n:删除序号为n的断点
- disable breakpoints:禁用断点
- enable breakpoints:启用断点
- info(或i) breakpoints:参看当前设置了哪些断点
- display 变量名:跟踪查看一个变量,每次停下来都显示它的值
- undisplay:取消对先前设置的那些变量的跟踪
- until X行号:跳至X行
- breaktrace(或bt):查看各级函数调用及参数
- info(i) locals:查看当前栈帧局部变量的值
- quit:退出gdb
1.3 示例:
(1)示例程序源码

编译源码时加上调试选项:
![]()
(2)运行gdb
(3)在gdb中查看代码

(4)在程序中加入断点,查看断点信息

(5)运行程序,输出断点处的堆栈信息

(6)单步运行,输出变量值
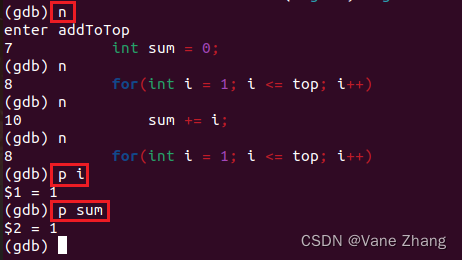
2 Analyzing coredump file by gdb
2.1 coredump文件简介
在Linux中,当进程崩溃或异常终止时,系统会将进程的内存状态写入一个coredump文件中,这个文件包含了进程崩溃时的内存映像,可以用于分析进程崩溃的原因。
2.2 coredump文件的存储路径
执行如下指令查询coredump文件的存储路径:
cat /proc/sys/kernel/core_pattern注意:默认值是core,表示当前目录,否则就是在指定目录下。
2.3 coredump产生的原因
造成程序coredump的原因有很多,这里总结一些常见情况:
(1) 内存访问越界
这种错误最常遇见,例如向strcmp函数中传入空指针导致的coredump
(2) 多线程程序使用了线程不安全的函数
多线程程序应该使用可重入的函数(带有"_r"后缀的函数)
(3) 多线程读写的数据未加锁保护
对于会被多个线程同时访问的全局数据,应该注意加锁保护,否则很容易造成coredump
(4) 非法指针
随意使用指针转换。一个指向一段内存的指针,除非确定这段内存原先就分配为某种结构或类型,否则不要将它转换为这种结构或类型的指针,而应该将这段内存拷贝到一个这种结构或类型中,再访问这个结构或类型。
(5) 堆栈溢出
不要使用大的局部变量(因为局部变量都分配在栈上),这样容易造成堆栈溢出,破坏系统的栈和堆结构,导致出现莫名其妙的错误。
2.4 使用gdb分析coredump文件
gdb是Linux中一个强大的调试工具,也可以用于分析coredump文件。使用gdb命令打开coredump文件,然后运行backtrace(bt)命令可以查看崩溃时的函数调用堆栈信息。
gdb -c [core_file] [exec_file] # -c 指定转储的 core 文件
(gdb) bt # 查看当前堆栈(断点所在的调用栈)注意:需要在Makefile中添加调试选项
2.5 实例:Mint mesh组网期间of_controller进程异常终止
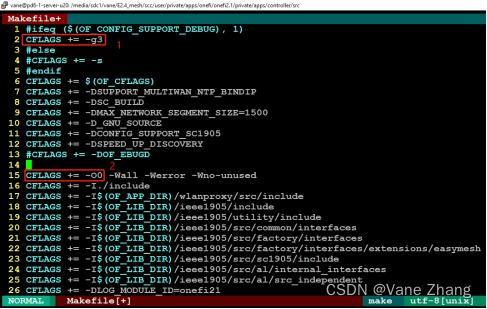
2.5.1 在Makefile中添加调试选项,如下图所示共修改了三处:
(1)添加”-g3”编译选项
① “-g1”, 不包含局部变量和与行号有关的调试信息,只能够用于回溯跟踪和堆栈转储之用。
② “-g2”, 此时产生的调试信息包括扩展的符号表、行号、局部或外部变量信息。
③ “-g3”, 包含g2中的所有调试信息,以及源代码中定义的宏。
(2)将”-O1”选项修改为”-O0”
使用”-O”选项时编译器会尝试减小代码尺寸,并去除相关的调试信息,因此这里修改为”-O0”,即不进行优化。
(3)屏蔽strip语句
strip经常用来去除目标文件中的一些符号表、调试符号表信息,以减小静态库、动态库和程序的大小。这里屏蔽strip语句,即不对生成的bin文件执行strip操作。
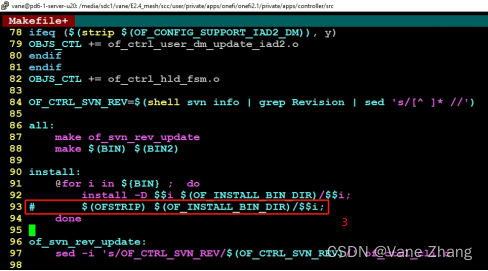
2.5.2 使用gdb分析生成的coredump文件:
(1)查看coredump文件的存储路径

(2)将coredump文件拿到编译环境的server上,放在of_controller生成的目录下

(3)进入docker(toolchain安装在docker中),然后执行:
gdb -c [core_file] [exec_file]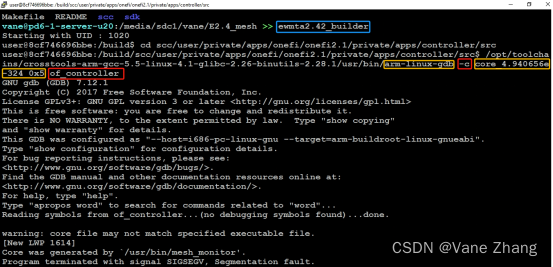
(4)在gdb中执行bt 指令,输出断点处的栈帧信息(进程崩溃时的栈帧信息)

结论:通过进程崩溃时的栈帧信息可知,进程在of_ctrl_user_dm_update_iad2.c文件第881行的of_ctrl_user_dm_ap_update()函数中发生异常。(最上面的栈帧表示最后调用的函数)