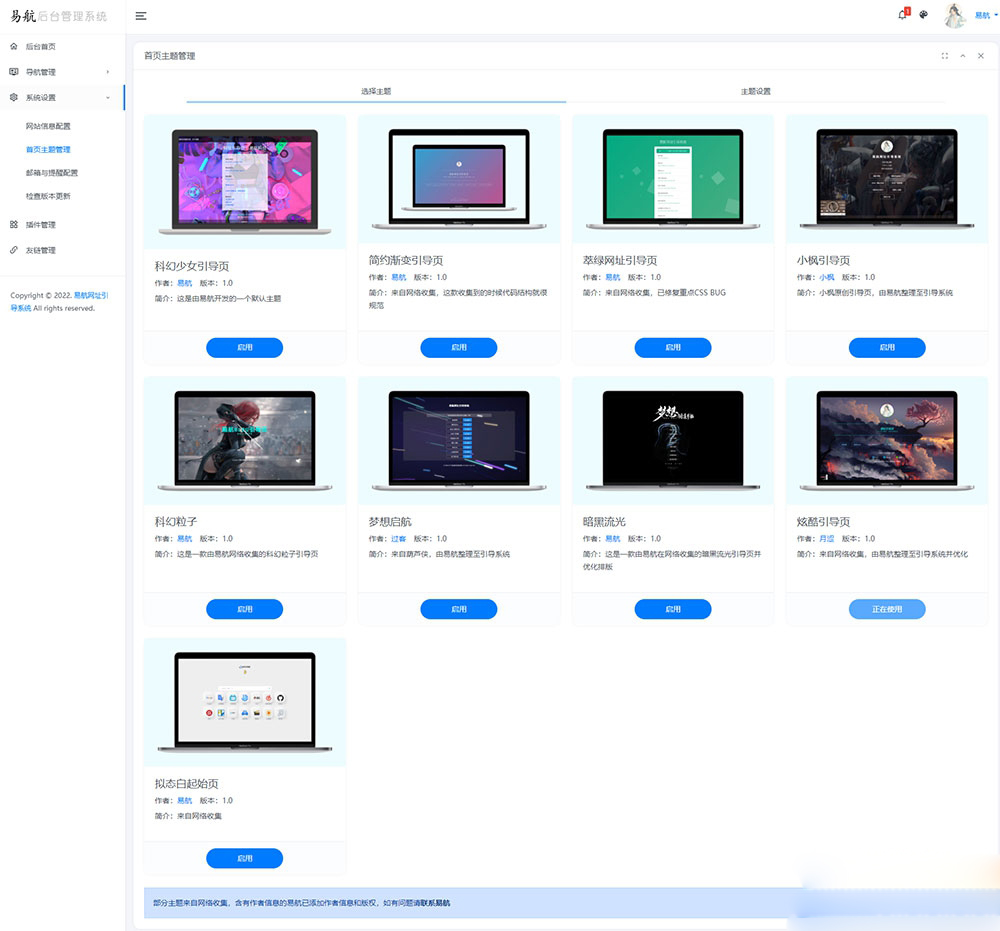
易航自主开发了一款极其优雅的易航网址引导页管理系统,后台采用全新的光年 v5 模板开发。该系统完全开源,摒弃了后门风险,可以管理无数个引导页主题。数据管理采用易航原创的JsonDb数据包,无需复杂的安装解压过程即可使用。目前系统内置了8套模板,并且可以进行自定义设置。另外,系统还内置了硬防洪和硬防墙插件,有效解决了域名安全的忧虑。
程序特色
后台采用全新的光年 v5 模板开发。
内置8款主题色,包括简约白、炫光绿、渐变紫、活力橙、少女粉、少女紫、科幻蓝和护眼黑。
可管理无数个引导页主题,并可以进行自定义设置,目前已内置了16套主题,并将持续增加。
支持单独开发各种插件,并可以进行自定义设置,目前已内置了七款实用插件。
无需繁琐的安装解压过程即可使用。
数据管理采用易航原创的JsonDb数据包。
主题内置了强大的$this语法,可以快速开发并保留著作版权。
对前台URL进行伪静态重写,更加友好对搜索引擎。
内置硬防洪和硬防墙插件,有效解决了域名安全的忧虑。
系统完全开源,摒弃了后门风险。
安装教程
PHP版本需≤8.0+。
需部署ThinkPHP伪静态规则。
后台地址:域名/admin。
初始账号:admin。
初始密码:123456。
源码下载:https://download.csdn.net/download/m0_66047725/88515399
源码下载2:关注我留言


![[机缘参悟-119] :一个IT人的反思:反者道之动;弱者,道之用 VS 恒者恒强,弱者恒弱的马太效应](https://img-blog.csdnimg.cn/106b29c1c1e6410782a24cdc464f812d.png)