目录
前言:
一、道家的核心思想
二、恒者恒强,弱者恒弱的马太效应
三、马太效应与道家思想的统一
3.1 大多数的理解
3.2 个人的理解
四、矛盾的对立统一
前言:
马太效应和强弱互转的道家思想,都反应了自然规律和社会规律,然而,他们描述了一对相反的规律和现象。马太效应表明恒者恒强,弱者恒弱的规律,而道家思想表明强弱互转才是“道”。那么这两种规律是矛盾的吗? 是统一的吗? 还是相互补充?如何解读他们呢?
一、道家的核心思想
阴阳互转和强弱互转是道家思想的两个重要方面。它们强调自然界中万物的互动、变化和平衡,具体表现为:
-
阴阳互转:道家认为宇宙是由阴阳两个相互对立又相互依存的力量构成的,它们不断地相互作用、转化、平衡,最终形成了万物。阴阳之间没有绝对的对立,而是相互转化和统一的过程。
-
强弱互转:道家认为一种事物的存在不是单一的、静止的,而是一个动态的、不断变化的过程。事物在一个时间内可能处于强势,而在另一个时间又可能处于弱势,这种强弱的变化是不可避免且自然的过程。
在道家看来,阴阳互转和强弱互转都是自然界中不断发生的现象。而且,由于这种互转关系的存在,一切事物都不是固定的、静止的,而是一个动态的、不断变化的过程。道家认为,遵循阴阳互转和强弱互转的规律,就能达到相对平衡、和谐、稳定的状态。因此,在宇宙和生命中,阴阳互转和强弱互转都是非常重要的哲学概念。
二、恒者恒强,弱者恒弱的马太效应
马太效应(Matthew effect)是指在某一领域中成功和优势的积累效应。这个术语来自于《圣经·马太福音》中的一句话:“凡有的,还要加给他,叫他有余;没有的,连他所有的也要夺过来”。
马太效应最初由社会学家罗伯特·金斯伯格(Robert K. Merton)于1968年提出,用来描述在科学研究领域中,已经取得成就的科学家更容易获得资源和机会,从而进一步扩大他们的研究影响力和成就,而那些刚刚起步或者较弱的科学家则更难获得同样的资源和机会,进一步加深了他们的劣势。
马太效应不仅存在于科学研究领域,也可以在其他领域中观察到,如学术研究、教育、运动竞技、经济等。这种效应的出现原因可能包括资源分配不均、人脉关系和社会认同等因素。
马太效应引起了人们对于社会不平等和资源分配不公的关注。一些人认为马太效应不利于社会的公正和平等,需要通过制度、政策或者其他措施来缓解不平等现象,为弱势群体提供更多的机会和资源,实现社会的公平与正义。
虽然,马太效应和"恒者恒强,弱者恒弱"之间不是相同的概念。马太效应是描述在某一领域中成功和优势的积累效应,强者更容易获得更多的资源和机会,进一步扩大他们的优势地位。而"恒者恒强,弱者恒弱"则暗示在一定的条件下,强者会保持其优势,而弱者则会持续处于劣势。
尽管在实际社会中存在一些现象可能与马太效应和"恒者恒强,弱者恒弱"相似,但它们并不是同一个概念。马太效应主要强调在某一特定领域中成功和优势的积累,而"恒者恒强,弱者恒弱"则更强调在某一特定条件下的持续差距。这两个概念在不同的背景和层面上有不同的解释和应用。
三、马太效应与道家思想的统一
3.1 大多数的理解
道家的阴阳互转思想和马太效应之间没有直接的对比。道家思想主要着眼于自然和宇宙的哲学观点和境界,而马太效应则是描述在某一特定领域中成功和劣势的积累效应。尽管两者在一些方面存在共通点,但它们的背景和应用领域不同,难以进行直接比较。
阴阳互转是道家哲学中的一种基本理念,认为宇宙万物都由阴阳两种相对而又统一的力量所构成,阴阳之间相互对立,又相互依存,不断转化、作用、平衡,从而塑造了万物世界的变化与发展。这一理念在道家哲学中扮演着重要的角色,被看作是万物的本质和宇宙间的基本规律。
相比之下,马太效应则主要是在社会、经济和教育领域中使用的一个概念。它强调在这些领域中成功和劣势的积累效应,认为开始就处于劣势地位的人往往很难从中获益,反而导致继续处于劣势。这一概念主要是描述某些现象和规律,而不是哲学思想或宇宙间的基本规律。
因此,道家的阴阳互转思想和马太效应难以进行直接的对比。它们的差异在于其在不同领域中的应用以及它们涉及的哲学观点的不同。需要指出的是,这两种理念都对人们的思考和理解提供了一些有用的思想,可以帮助我们更好地理解宇宙和生命中的规律和变化。
3.2 个人的理解
道家的阴阳互转思想是谈到的宏观和长期效应,是一个系统的长期平衡。
马太效应谈到的是短期的聚合现象,聚合是自然界和社会普遍的现象,然后,聚合是有终点的,当聚合体的规模大之前,符合马太效应的规律,然后,当规模大到一定的程度后,又会符合道家的阴阳互转的规律,任何聚合的规模体,包括人、生命体、星体。这些聚合体,最终都会走向死亡和分解。
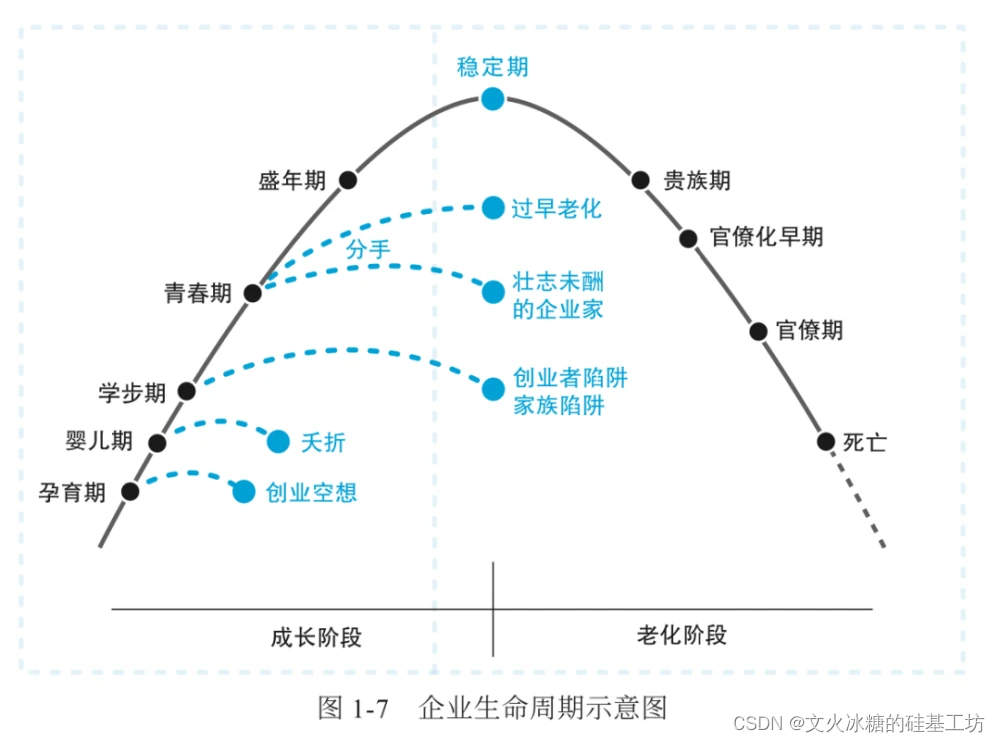

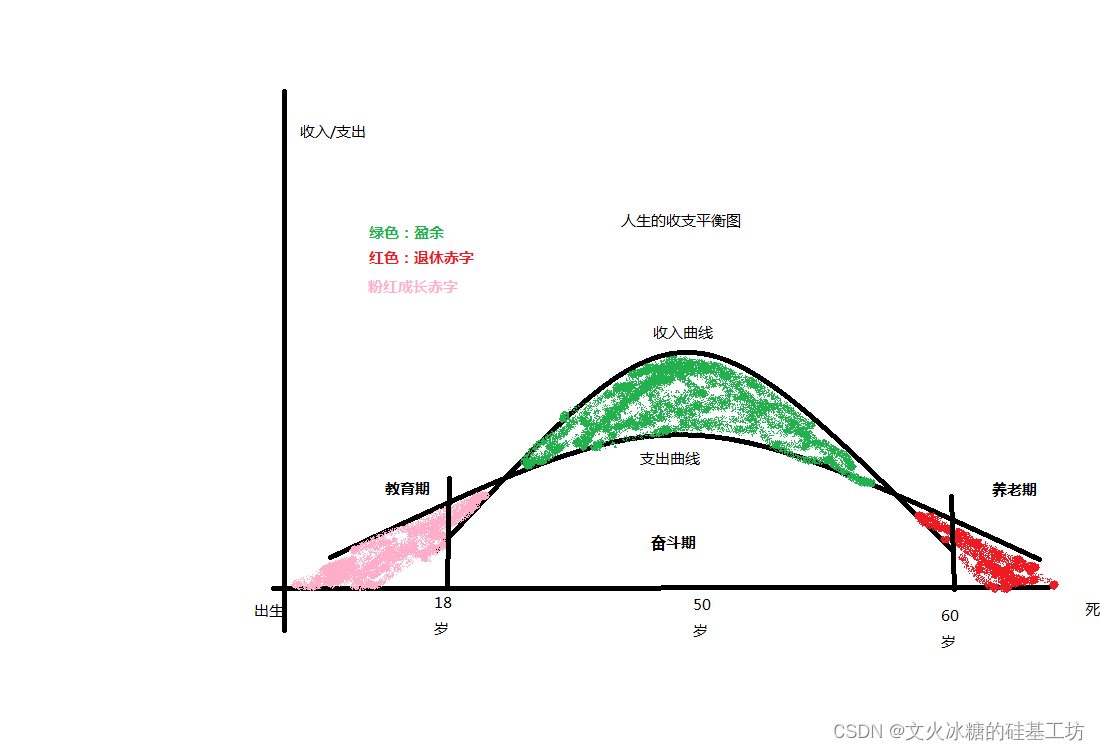
上升期:马太效应与强者恒强规律
下降期:马太效应与强者恒弱规律
整个生命期:道家的强弱互转规律、生死规律。
至此,马太效应和道家思想不再相互矛盾对立,而是统一的。
四、矛盾的对立统一

矛盾的对立统一是一个重要的辩证法观念,它是指任何事物内部都含有着相互矛盾的各个方面,并在相互斗争和斗争中达到动态的统一和平衡。这个观念最初由哲学家黑格尔提出,后来由马克思和恩格斯进一步发展和运用于他们的哲学体系中。
根据辩证法的观点,任何事物都包含着相互矛盾的对立面。这些对立面之间不是简单的互斥关系,而是通过相互作用和斗争来推动事物的发展和变化。例如,存在着生与死、积极与消极、阴与阳、利益与矛盾等对立面。这些对立面相互依存、相互制约,同时又通过相互作用达到动态的统一。
矛盾的对立统一的核心思想是要看待事物和现象的复杂性,不将事物简化为单一的、静止的存在,而是要看到其中的多样性和变化过程。事物的发展和变化是通过矛盾的对立面之间的斗争和调和来实现的。在这个过程中,一方面的力量逐渐消退,而另一方面的力量则逐渐取得优势,最终实现了对立面的统一。
总而言之,矛盾的对立统一是指任何事物内部都存在着相互矛盾的各个方面,通过相互斗争和斗争达到动态的统一。这一观念在辩证法思想中占据重要地位,被广泛应用于哲学、社会科学和自然科学等领域。