目录

一、异或运算符的运用&&leetcode136

异或运算符 a ^ b ^ b = a

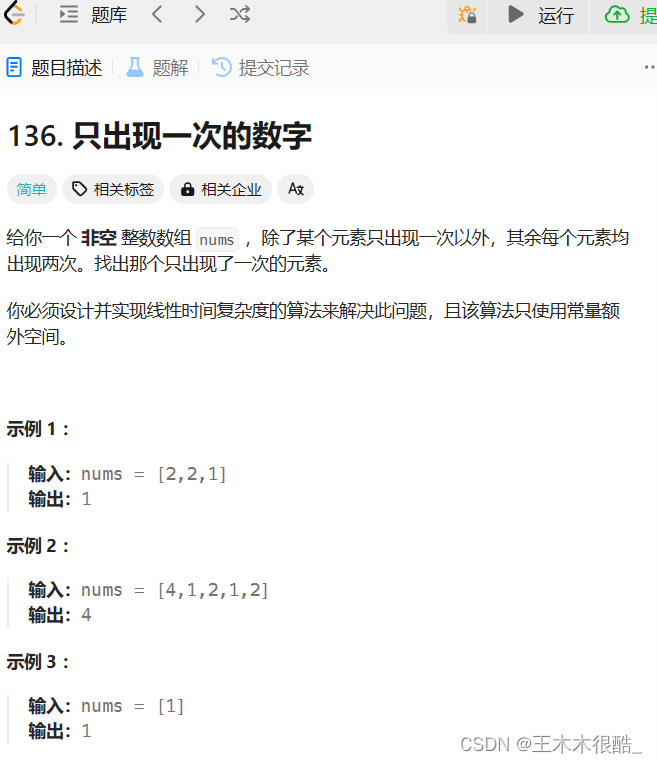
leetcode136

二、n & (n - 1)&&leetcode133

n & (n - 1):消除n最右边的一个1

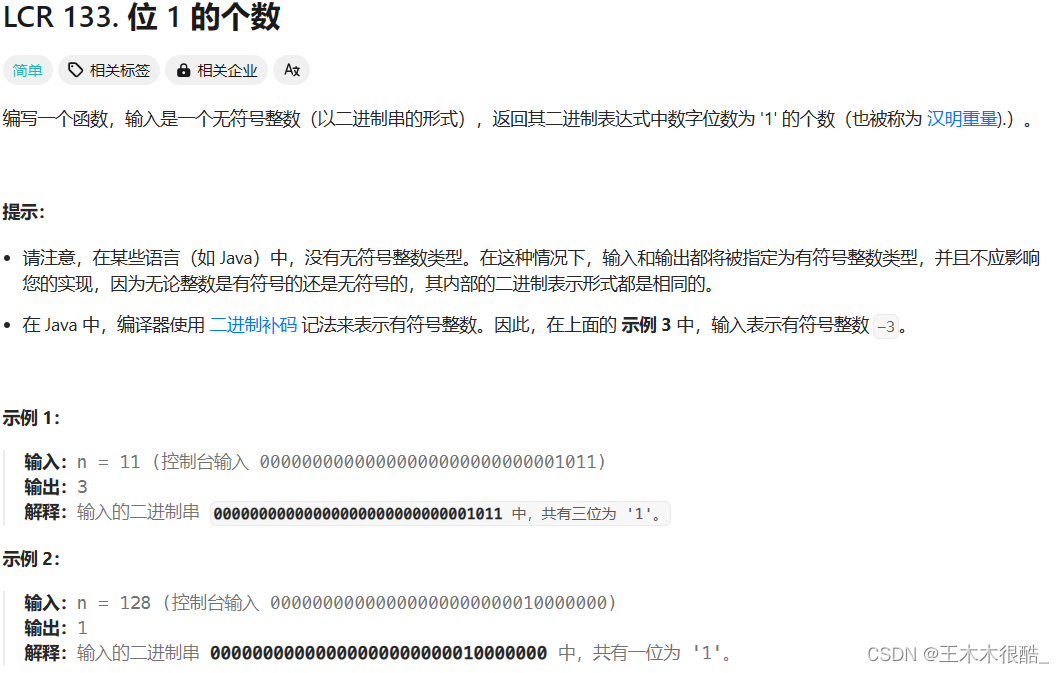
leetcode133/剑指offer15

三、m的n次方（n是正整数）

常规写法

二进制的快速幂算法

---

一、异或运算符的运用&&leetcode136

异或运算符 a ^ b ^ b = a

1）两个数相同，异或的结果为0。

2）任何数和0异或结果都等于它本身。

3）异或支持交换律。

leetcode136

//把所有的数异或，两个相同的元素就会被消掉
class Solution {
    public int singleNumber(int[] nums) {
        int res = 0;
        for(int i = 0; i < nums.length; i++){
            res = res ^ nums[i];
        }
        return res;
    }
}

二、n & (n - 1)&&leetcode133

n & (n - 1):消除n最右边的一个1

n = 10100

n & (n - 1) = 10000   

原理是借位： 10100 - 1 = 10011     10100 & 10011 = 10000

leetcode133/剑指offer15

public class Solution {
    // you need to treat n as an unsigned value
    public int hammingWeight(int n) {
        int sum = 0;
        while(n != 0){
            n = n & (n - 1);
            sum++;
        }
        return sum;
    }
}

三、m的n次方（n是正整数）

常规循环写法

 

二进制的快速幂算法

假设n = 13 = 1101 = 1 + 4 + 8

那么 m ^ 13 = m^1 * m^4 * m^8 = m ^ 1 * m^100 * m^1000

判断二进制有多少个1。这是快速幂算法来计算幂。它的基本思想是将指数n分解为若干个二进制位，然后根据每一位的值来决定是否将当前的底数m乘到结果中。具体来说，如果n的二进制表示的最后一位是1，则将m乘到结果中；然后将m平方，以便在下一次循环中进行计算。最后，通过不断地将n右移一位（即除以2），直到n变为0为止。最终返回的结果就是m的n次方。

//n是正整数
int pow(int m, int n) {
    int sum = 1; // 初始化结果为1
    int tmp = m; // 将m的值赋给临时变量tmp

    while (n != 0) {
        if (n & 1 == 1) {
            sum *= tmp; // 如果n的二进制表示的最后一位是1，则将tmp乘到sum上
        }
        tmp *= tmp; // 将tmp平方，以便在下一次循环中进行计算
        n = n >> 1; // 将n右移一位，相当于除以2
    }

    return sum; // 返回最终的结果
}