图神经网络是一种用于以图形式呈现的数据的神经网络。图形是由顶点（节点）和边组成的空间结构。有许多结构表示为图形：三维空间（x，y，z）中的结构，如物质分子（例如咖啡因）、蛋白质（由氨基酸组成）、DNA、计算机网络以及社交网络等结构。以下是一些使用 Wolfram Mathematica 制作的例子：

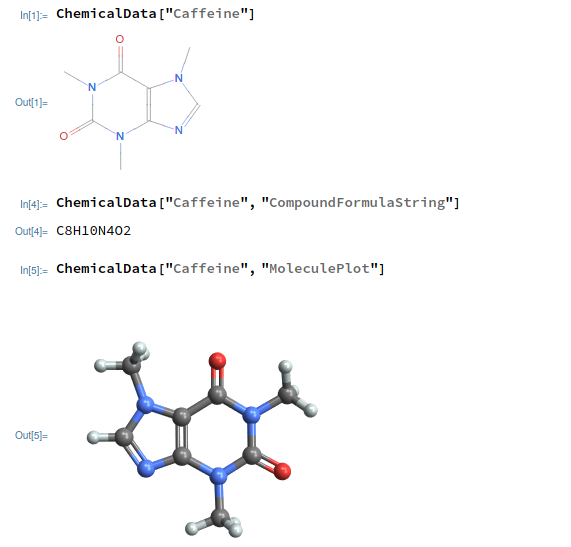
        咖啡因的分子结构

        蛋白

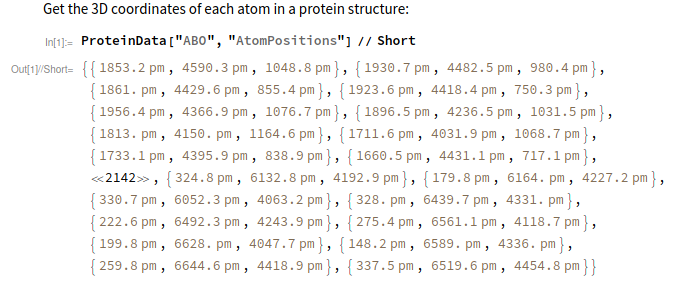
        蛋白质中原子的 XYZ 坐标

社交网络

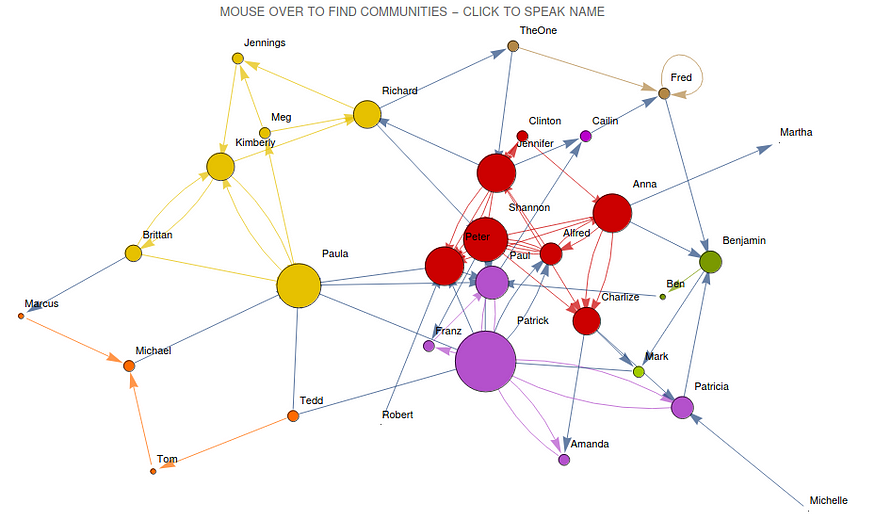
        社交网络社区

        基本上，每个节点代表一个人、一个原子、一个金融交易，这些节点通过边连接，在这些实体之间建立关系。在人与人之间，这可能是领带的强度、社交距离、亲密程度。在分子结构中的原子中，这些边缘可能是共价键。在金融交易中，这些边缘可以定义某人与欺诈交易的距离。

        考虑到社交网络的例子（如上图），我们有密集连接的人集群，可能与“影响者”有关，也有薄弱环节（弱纽带），它们连接不同的人群，允许信息的多样性。当我们亲自或通过社交媒体相互交谈时，我们的信息会通过这个社交网络传播，并且可能会受到其内容的变形和误解的影响。原子及其电磁特性也会发生同样的情况：其他原子离得越近，它们受这些电磁特性的影响就越大。因此，经过一段距离后，这种影响会逐渐消失。此外，如果允许这种影响渗透到所有网络结构中，则由于饱和，整个网络可能会收敛到单一状态。

三、图网络的向量模型

        但是，我们如何才能用数学方式来表示这些复杂的关系，以便能够对这些相互作用进行建模呢？首先，我们应该定义每个参与者之间的联系。这是通过邻接矩阵完成的，其中相同的个体被放置在该矩阵的行和列中：

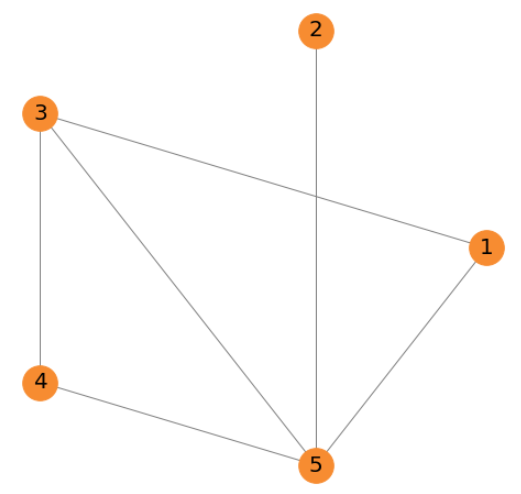
        基于邻接矩阵的网络结构

        此邻接矩阵中的每个数字 1 都表示一个连接。我们有一个 5 x 5 矩阵，其中节点 1 到 5 分别放置在线和列中。所以，如果你拿个体 2，他只与个体 5 相连。个体 1 连接到个体 3 和 5，依此类推。为了绘制这个网络，我使用了以下代码：

import numpy as np
import networkx as nx

Adj = np.array(
    [[0, 0, 1, 0, 1],
     [0, 0, 0, 0, 1], 
     [0, 0, 0, 1, 1], 
     [0, 0, 1, 0, 1], 
     [1, 1, 0, 0, 0]]
)
g = nx.from_numpy_array(Adj)
pos = nx.circular_layout(g)

fig, ax = plt.subplots(figsize=(8,8))
nx.draw(g, pos, with_labels=True, 
    labels={i: i+1 for i in range(g.number_of_nodes())}, node_color='#f78c31', 
    ax=ax, edge_color='gray', node_size=1000, font_size=20, font_family='DejaVu Sans')

        现在我们将邻接矩阵乘以由行数组成的向量。因此，我们将得到一个 5 x 5 矩阵乘以 5 x 1 向量。这意味着 n x p 乘以 p x m 将得到一个 n x m 向量。在本例中，5 x 1 向量：

H = Adj @ np.array([1,2,3,4,5]).reshape(-1,1)

        请注意，为了进行此乘法，您需要将 p x m 向量转置为 [1,2,3,4,5]，并逐个元素乘以邻接矩阵和总和的那行的每个元素。结果是相连邻域的总和。按住 H 一会儿。 

        现在我们将找到对角线度矩阵，它由对角线中的邻域大小组成，即矩阵中每一列的总和：

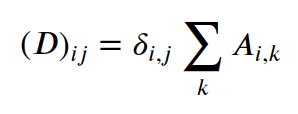
D = np.zeros(Adj.shape)
np.fill_diagonal(D, Adj.sum(axis=0))

对角线度矩阵

现在，我们将为每个边分配一个权重。我们通过将恒等矩阵除以对角度矩阵来做到这一点。

D_inv = np.linalg.inv(D)

倒置度矩阵

通过将倒置的 D 乘以邻接矩阵，我们将得到一个平均的邻接矩阵：

        平均邻接矩阵

        当我们处理一个没有单个值的节点，而是特征向量的集合时，平均的概念非常重要，就像图卷积网络一样。

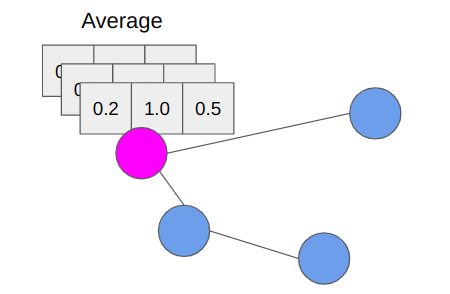
        但是，我们真正想要操作的是消息传递算法，如下所示：

        反复应用的帽子将允许信息在图网络中流动。假设波浪号等于邻接矩阵加单位矩阵，我们有：

g = nx.from_numpy_array(Adj)
Adj_tilde = Adj + np.eye(g.number_of_nodes())

        现在我们需要创建 D 波浪号的平方根。我们创建一个零矩阵，并将邻接矩阵波浪号的线和值相加。

D_tilde = np.zeros_like(A_tilde)
np.fill_diagonal(D_tilde, A_tilde.sum(axis=1).flatten())

        然后我们计算 D 波浪号的平方反比根：

D_tilde_invroot = np.linalg.inv(sqrtm(D_tilde))

        现在我们已经有了 A 波浪号，以及 D 波浪号的平方反比根，我们可以计算出 A 帽子：

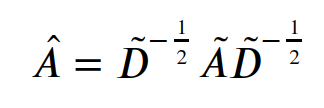
A-hat（帽子）的程序表示：

A_hat = D_tilde_invroot @ A_tilde @ D_tilde_invroot

        请注意，numpy 中的 @ 与 matmul 的意思相同。

A-hat 帽子的结果

        现在我们将实现消息传递算法。让我们从我们拥有的消息向量 （H） 开始，检查它在图网络中的流动方式。我们知道：

H = Adj @ np.array([1,2,3,4,5]).reshape(-1,1)

        现在我们让信息流在图网络中：

epochs = 9
information = [H.flatten()]
for i in range(epochs):
    H = A_hat @ H
    information.append(H.flatten())

四、图神经网的可视化 

        让我们看看这个热图中的信息流。注意每个个体（x 轴）如何随时间（y 轴）获取或丢失信息。

import matplotlib.pyplot as plt

plt.imshow(information, cmap='Reds', interpolation='nearest')
plt.show()

        让我们把它画出来：

fig, ax = plt.subplots(figsize=(12, 12))
from time import time

for i in range(0,len(information)):
    colors = information[i]
    
    nx.draw(
    g, pos, with_labels=True, 
    labels=node_labels, 
    node_color=colors*2, 
    ax=ax, edge_color='gray', node_size=1500, font_size=30, font_family='serif',
    vmin= np.array(information).min(), vmax=np.array(information).max())
    plt.title("Epoch={}".format(i))
    plt.savefig('/home/user/Downloads/message/foo{}.png'.format(time()), bbox_inches='tight', transparent=True)

import glob
from PIL import Image

fp_in = "/home/user/Downloads/message/foo*.png"
fp_out = "/home/user/Downloads/message100_try.gif"

img, *imgs = [Image.open(f) for f in sorted(glob.glob(fp_in))]
img.save(fp=fp_out, format='GIF', append_images=imgs,
         save_all=True, duration=1200, loop=0)

        从视觉上看，图网络中的信息流在每个时期都如下所示：

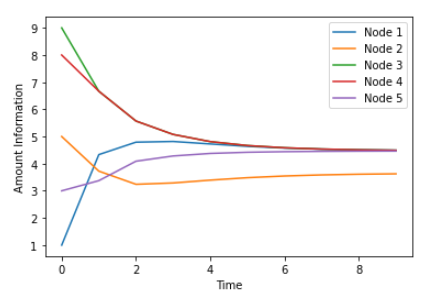
        在下图中，我们可以看到网络的每个节点随时间推移有多少信息。请注意节点 1、3、4 和 5 的收敛：

        有关消息传递算法在基于代理的模型中的实际应用，请参阅我在 COMSES 上使用 Python 和 NetLogo 制作的模型：鲁本斯·津布雷斯