一、问题描叙
设有n=2^k个运动员,要进行网球循环赛。现在要设计一个满足以下要求的比赛日程表
- 每个选手必须与其他n-1个选手各赛一场
- 每个选手一天只能赛一次
- 循环赛一共进行n-1天
二、问题分析
按此要求可将比赛日程表设计成n行n-1列的表,在表中第 i 行和第j 列处填入第 i 个选手在第 j 天所遇到的对手。
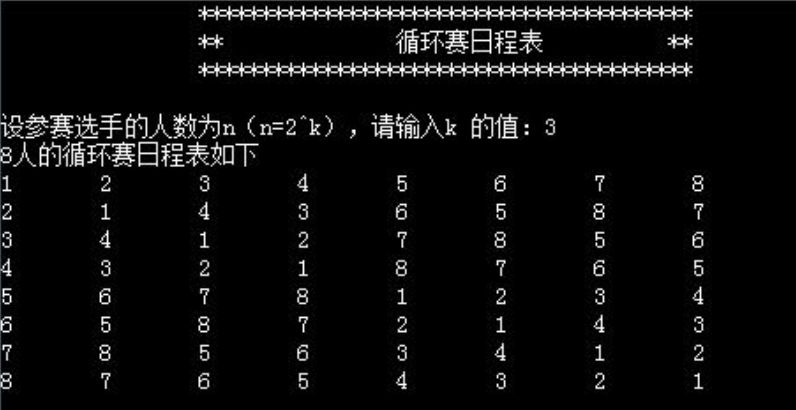
例如,当选手的人数为8人时,其比赛日程表如下图
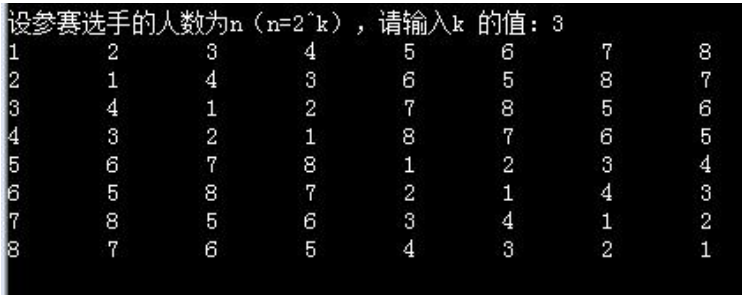
算法分析:
按分治策略,我们可以将所有的选手分为两半,则n个选手的比赛日程表可以通过n/2个选手的比赛日程表来决定。递归地用这种一分为二的策略对选手进行划分,直到只剩下两个选手时,比赛日程表的制定就变得很简单。这时只要让这两个选手进行比赛就可以了。如上图,所列出的正方形表是8个选手的比赛日程表。其中左上角与左下角的两小块分别为选手1至选手4和选手5至选手8前3天的比赛日程。据此,将左上角小块中的所有数字按其相对位置抄到右下角,又将左下角小块中的所有数字按其相对位置抄到右上角,这样我们就分别安排好了选手1至选手4和选手5至选手8在后4天的比赛日程。依此思想容易将这个比赛日程表推广到具有任意多个选手的情形。
算法实现步骤:
(1)当k=1时,即人数为2人,此情况为最简单的情况
此表为:

(2)当k=2时,人数为4人,循环表为
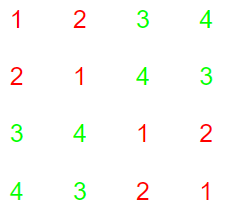
(3)当k=3时,人数为8人,此时循环表为
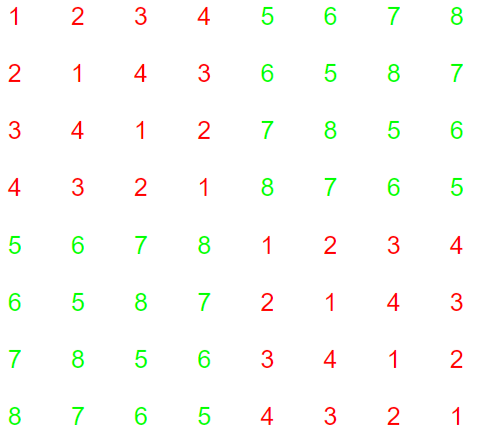
以此类推,我们不难发现,我们可以用分治的方法实现,现自顶向下分解,直到分解到最简单的情况,即人数为2人,这时就可以两两比赛,表的填充为对角填充的方式,然后再自底向上填充表格,具体的看上面的k=1,k=2,k=3时形成的循环表就很好理解了。
三、代码示例
#include<stdio.h>
#include<math.h>
#define N 50
void GameTable(int k,int array[][N]);
void print(int k,int array[][N]); //输出二维数组
main()
{
int k;
int array[N][N];
printf("\t\t****************************************\n");
printf("\t\t**\t\t循环赛日程表 **\n");
printf("\t\t****************************************\n\n");
printf("设参赛选手的人数为n(n=2^k),请输入k 的值:");
do
{
scanf("%d",&k);
if(k!=0)
{
GameTable(k,array);
print(k,array);
}
else
printf("您输入的数据有误,请重新输入");
}while(k!=0);
}
void GameTable(int k,int array[][N])//数组下标从1开始
{
int i,j,s,t;
int n=1;
for(i=1;i<=k;i++)
n*=2; //求总人数
for(i=1;i<=n;i++)
array[1][i]=i; //第一行排1-8
int m=1; //用来控制每一次填表时i行j列的起始填充位置
for(s=1;s<=k;s++) //s指对称赋值的总循环次数,即分成几大步进行制作日程表
{
n=n/2;
for(t=1;t<=n;t++) //t指明内部对称赋值的循环次数
for(i=m+1;i<=2*m;i++)
for(j=m+1;j<=2*m;j++)
{
array[i][j+(t-1)*m*2]=array[i-m][j+(t-1)*m*2-m]; //右上角等于左上角的值
array[i][j+(t-1)*m*2-m]=array[i-m][j+(t-1)*m*2]; //左下角等于右上角的值
}
m*=2;
}
}
void print(int k,int array[][N])
{
int i,j;
int num=pow(2,k);
printf("%d人的循环赛日程表如下\n",num);
for(i=1;i<=num;i++) //输出二维数组
{
for(j=1;j<=num;j++)
{
printf("%d\t",array[i][j]);
}
printf("\n");
}
}
四、程序结果展示