个人主页:仍有未知等待探索_C语言疑难,数据结构,小项目-CSDN博客
专题分栏:算法_仍有未知等待探索的博客-CSDN博客
为什么需要高精度算法?
由于c++不能进行位数过高的数据运算,所以要通过模拟数组来进行运算,首先是加法。通过char或string型数据输入字符来模拟数字的输入,数组下表对应的元素应当是处于同一位置的数字,下标相同的两个元素相加表示的既是结果。
目录
一、高精度加法
1、思路
2、代码
二、高精度乘法
1、思路
2、代码
一、高精度加法
1、思路
其实高精度加法和普通的加法思路没有什么区别。就是个位数先相加,然后判断进位,在把进位进行相加。最后得到结果。
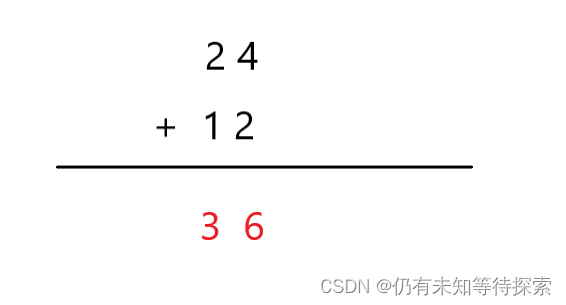
从个位开始进行相加,进位操作。(通过数组进行存储)
2、代码
#include<iostream>
#include<string>
using namespace std;
const int N = 510;//数字最大可以存储509位的数字
int a[N];//要相加的数字
int b[N];//要相加的数字
int c[N];//得到的结果
int main()
{
string str1;//要想加的数字
string str2;//要相加的数字
cin >> str1;
cin >> str2;
//将str1和str2进行逆置存放
for (int i = 0; i < str1.size(); i++)
a[str1.size() - 1 - i] = str1[i] - '0';
for (int i = 0; i < str2.size(); i++)
b[str2.size() - 1 - i] = str2[i] - '0';
//得到最大的位数
int ans = max(str1.size(), str2.size());
for (int i = 0; i < ans; i++) {
c[i] += a[i] + b[i];//相加
c[i + 1] = c[i] / 10;//进位
c[i] %= 10;//如果1位数大于10,对其进行取余
}
ans += 1;//避免最大位数相加完之后有进位:比如说500+500,5+5=10,要进位
//去除前导0
if (c[ans - 1] == 0 && ans > 1)
ans -= 1;
//输出
for (int i = 0; i < ans; i++)
cout << c[ans - 1 - i];
return 0;
}
二、高精度乘法
1、思路
- 按照常规的高精度乘法的思路,分别先用两个数组逆序存储两数,方便计算。
- 结果的长度必然不会超过两数的长度之和。
- 进行乘法运算时,我们可以先不用考虑进位,按照常规思路直接算。
- 计算完成后,处理数组中结果大于或等于10的位置,即向前进位。
- 最后,处理前导零,将结果逆序输出。
高精度乘法和竖式运算的乘法思路是一样的。如图所示:
根据上面的规律可以知道下图的公式。
2、代码
#include<iostream>
using namespace std;
const int N = 2000;
int m[N];//要算的数
int n[N];//要算的数
int ans[2 * N];//所得的答案
int main() {
string a, b;//字符串输入
cin >> a >> b;
int la = a.size();//a的字符串长,也就是乘数的位数
int lb = b.size();//b的字符串长,也就是乘数的位数
int i = 0, j = 0;
//逆序存入数组中
for (i = 0; i < la; i++) {
m[i] = a[la - i - 1] - '0';
}
//逆序存入数组中
for (j = 0; j < lb; j++) {
n[j] = b[lb - j - 1] - '0';
}
//根据公式进行计算
for (i = 0; i < la; i++) {
for (j = 0; j < lb; j++) {
ans[i + j] += m[i] * n[j];
}
}
//上述仅进行了计算各个位的数,没有考虑进位
//下面循环考虑进位
//ns为答案的位数,由例子可知,答案的位数的最小值为la+lb-1
int ns = la + lb - 1;
for (i = 0; i < ns; i++) {
//各位大于9时,才考虑进位的问题
if (ans[i] > 9) {
ans[i + 1] += ans[i] / 10;
ans[i] %= 10;
}
//如果i+1进位大于ns,ns要进行更新
if (i + 1 > ns) {
ns++;
}
}
//逆序打印
//考虑先导0的问题
if (ans[i] == 0 && ns > 1)
ns--;
for (i = ns; i >= 0; i--) {
cout << ans[i];
}
return 0;
}
谢谢大家的支持!


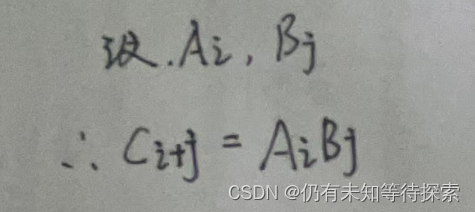


![[AutoSar]CP autosar 面试题](https://img-blog.csdnimg.cn/5c9e281802be4435bb6977130cd772a7.png)


![[AutoSar]工程中的cpuload陷阱(三)测试](https://img-blog.csdnimg.cn/8b3a8e931b98456dab25e5a2edd81406.png)