---

前言

ZC 序列和 m 序列是数字通信中常用的两种序列，在编码和解码过程中起到重要的作用。本文作为 ZC 序列学习笔记，主要研究 ZC 序列的一些性质，并通过 MATLAB 对其进行仿真验证。

---

一、ZC 序列理论

1、基本概念

ZC 序列（Zadoff-Chu 序列）是一种具有良好性质的离散序列，它是一种复数序列，在通信系统中广泛应用。它由 Zadoff 和 Chu 于 1964 年提出，是一种特殊的线性调频脉冲压缩序列。ZC 序列常用于通信系统中的同步和信道估计等方面。

• ZC 序列的自相关性是指序列与其自身进行相关运算后的结果。自相关性能够体现序列的周期性和重复性，对于同步和信道估计非常重要。
• ZC 序列的互相关性是指序列与其他序列进行相关运算后的结果。互相关性能够体现序列之间的相似程度，对于信道估计和多用户检测等方面有着重要作用。

ZC 序列常用于各种无线通信系统中，如 LTE（Long Term Evolution）、WiMAX（Worldwide Interoperability for Microwave Access）、GNSS（Global Navigation Satellite System）等。它们被广泛应用于信号处理和通信领域，以提高系统性能和可靠性。

2、表达式

ZC 序列常用于随机接入（Random Access）中以生成 preamble 序列，其表达式如下图所示：

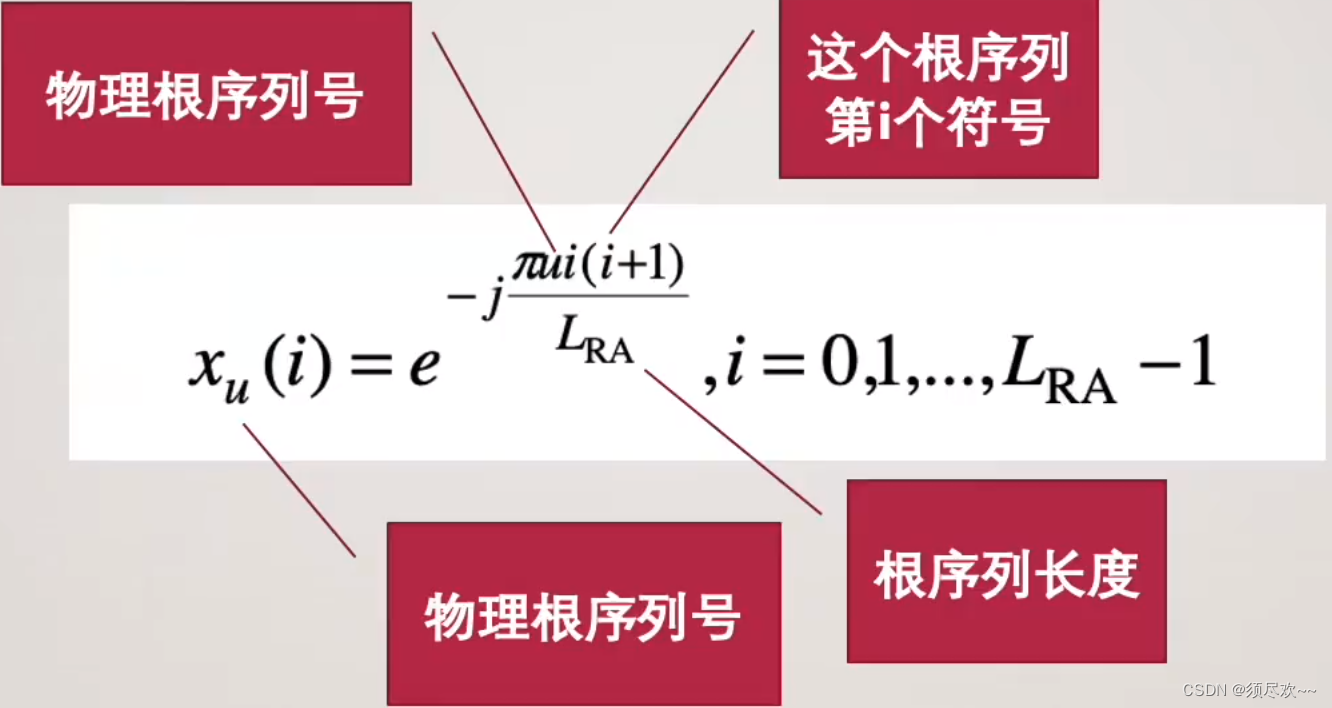
ZC 序列有两个重要的参数：

• 根索引（root index）：对应上图中物理根序列号 $u$，$u$ 是由逻辑根序列号查表获取；
• ZC 序列的长度：对应上图中根序列长度 $L_{RA}$，一定得是奇数（常常是质数）；

对于任意 ZC 序列，在长度 $L_{RA}$ 和根序列 $u$ 的取值确定的情况下，便可确定根序列 $i$。

注意到：每个 ZC 序列的长度为 $L_{RA}$，而ZC序列的序列空间大小为 $L_{RA}-1$，即一共有 $L_{RA}-1$ 个 ZC 序列。

我们可以发现，ZC 序列的值是一个复数，由欧拉公式 $e^{j\alpha }=cos(\alpha )+jsin(\alpha )$，即可得到该复数的实部和虚部，除此之外，还可以发现它的幅值恒为 1，其实在复数坐标系中，它都是在单位圆上。

3、ZC 序列一些定义

①、自相关

离散时间序列的自相关函数定义为：
$$R_n=\sum _{n=-\infty }^{\infty }x[k]x^{\ast }[k+n]$$

• $x[k]$ 为调制序列；
• $x^{\ast }[k+n]$ 为 $x[k]$ 时延信号的共轭。

②、循环移位

一个长度为 $N$ 的有限长序列 $x[n]$，其 m 次循环移位公式如下：
$$x^m[n]=x[(n+m)modN]，m=0,1,2,...,N-1$$
一共有 $N$ 个循环移位序列（包括本身）。

③、循环自相关

循环自相关也叫周期自相关，长度为 $N$ 的有限长序列 $x[n]$ 的序列循环自相关公式为：
R 0 = ∑ n = 0 N − 1 x [ n ] x ∗ [ n