[ATC复盘] abc329 20231118
- 总结
- A - Spread
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- B - Next
- 1. 题目描述
- 2. 思路分析-
- 3. 代码实现
- C - Count xxx
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- D - Election Quick Report
- 2. 思路分析
- 3. 代码实现
- E - Stamp
- 2. 思路分析
- 3. 代码实现
- F - Colored Ball
- 2. 思路分析
- 3. 代码实现
- 六、参考链接
总结
- 前6题除了E都挺水的。
- A 语法题。
- B 排序。
- C dp计数。
- D 贪心
- E dp
- F 启发式合并(模拟)

A - Spread
链接: A - Spread
1. 题目描述
把输入的字符串每个字符中间加空格输出。
2. 思路分析
- join
3. 代码实现
def solve():
s, = RS()
print(' '.join(s))
B - Next
链接: B - Next
1. 题目描述
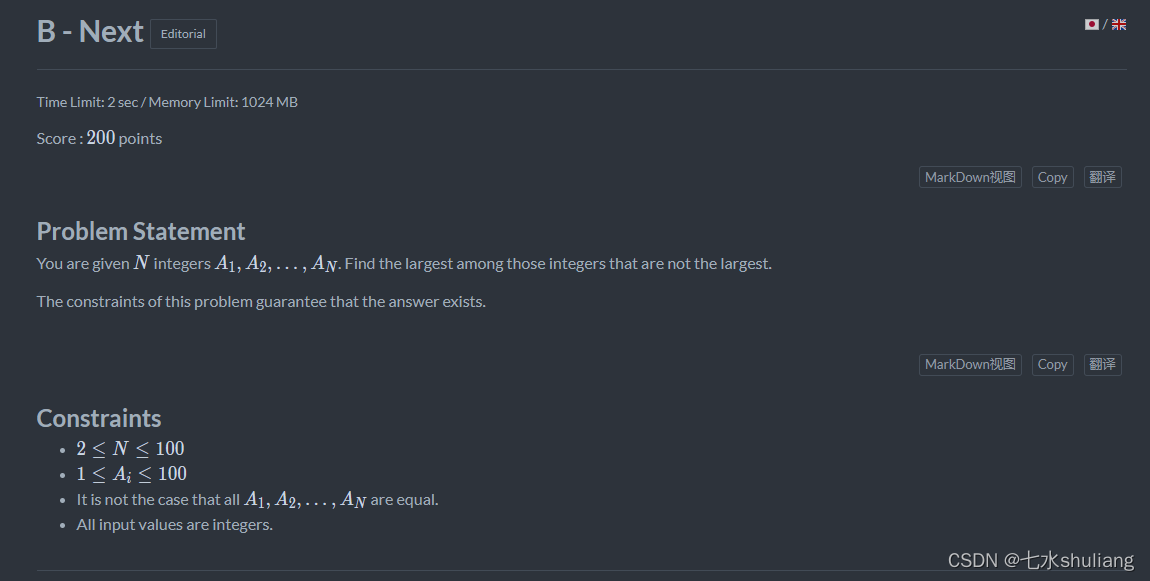
2. 思路分析-
- 题目问出了最大之外,最大的数是哪个。
- 就是第二大。排序即可。
3. 代码实现
def solve():
n, = RI()
a = sorted(set(RILST()))
print(a[-2])
C - Count xxx
链接: C - Count xxx
1. 题目描述
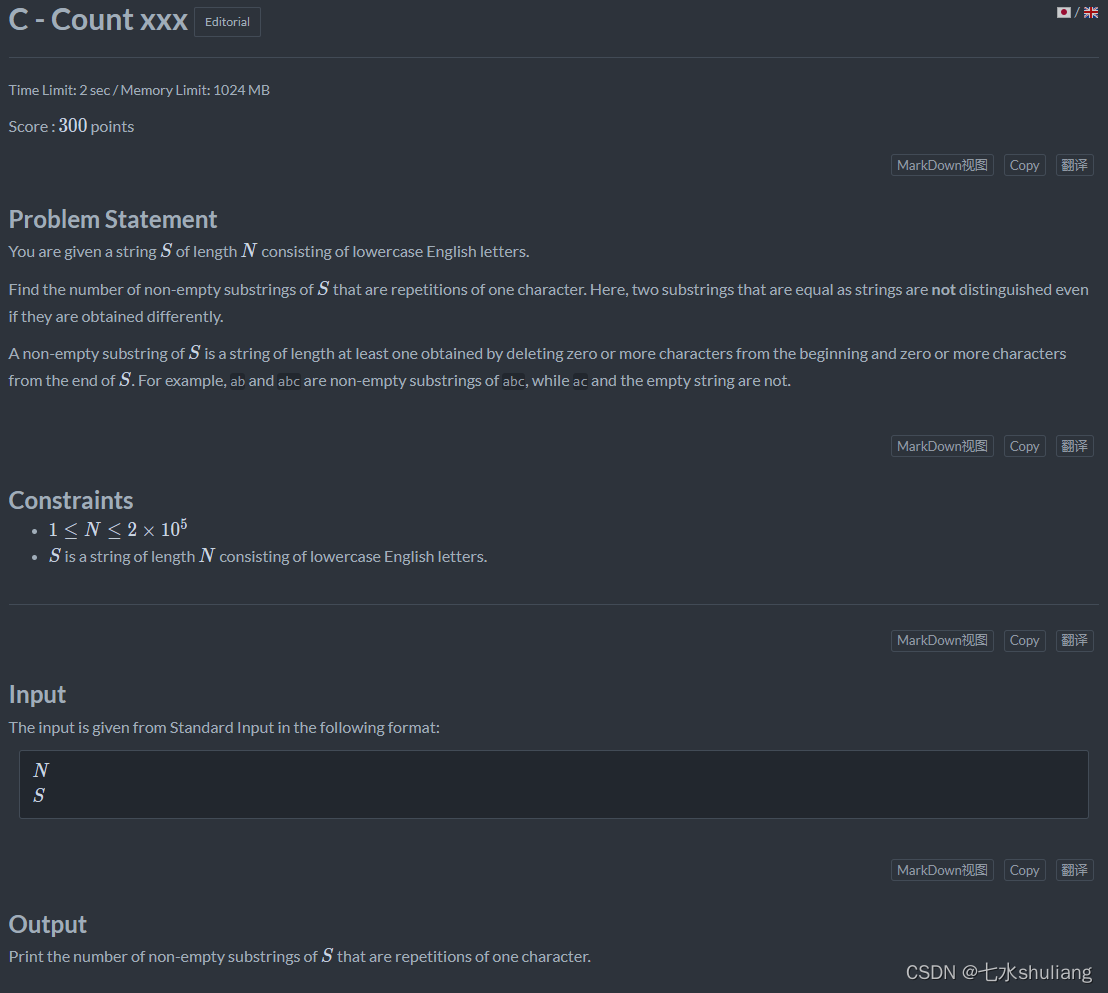
2. 思路分析
- 问有多少种连续相同字符的子串。如果字母a最长连续8个,那么a的连续子串有8种。
- 那么把每种字母最长连续计数即可,我习惯用dp处理。
3. 代码实现
def solve():
n, = RI()
s, = RS()
cnt = Counter([s[0]])
f = [1] * n
for i in range(1, n):
if s[i] == s[i - 1]:
f[i] += f[i - 1]
cnt[s[i]] = max(cnt[s[i]], f[i])
print(sum(cnt.values()))
D - Election Quick Report
链接: D - Election Quick Report
2. 思路分析
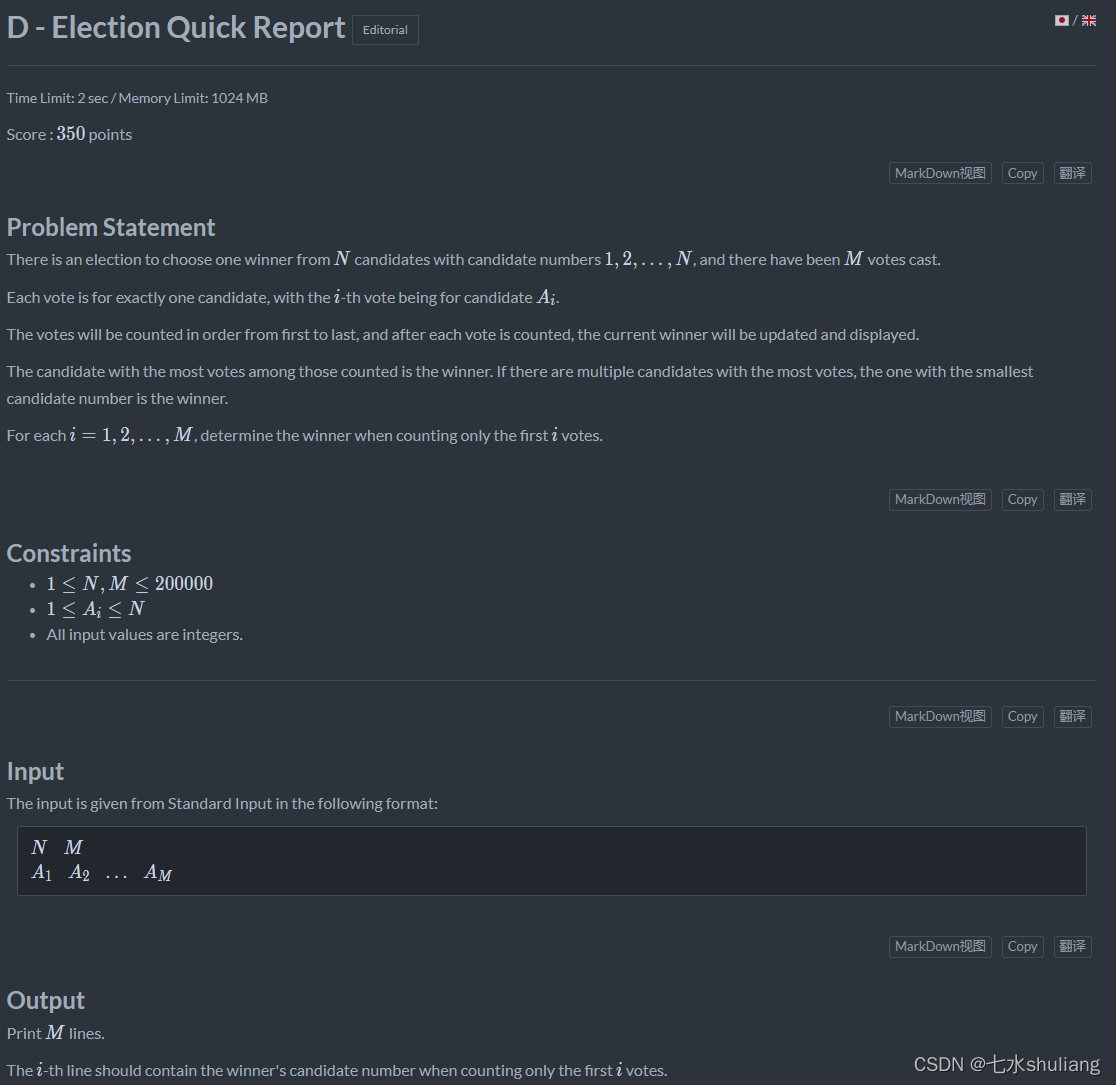
按顺序唱票,问当前获胜者是谁,平票取id最小的。
- 直接计数,更新最大计数即可,注意id也一起比较。
3. 代码实现
def solve():
n, m = RI()
a = RILST()
cnt = [0 for _ in range(n + 1)]
win = [0, 0] # 计数,-下标
for v in a:
cnt[v] += 1
win = max(win, [cnt[v], -v])
print(-win[1])
E - Stamp
链接: E - Stamp
2. 思路分析
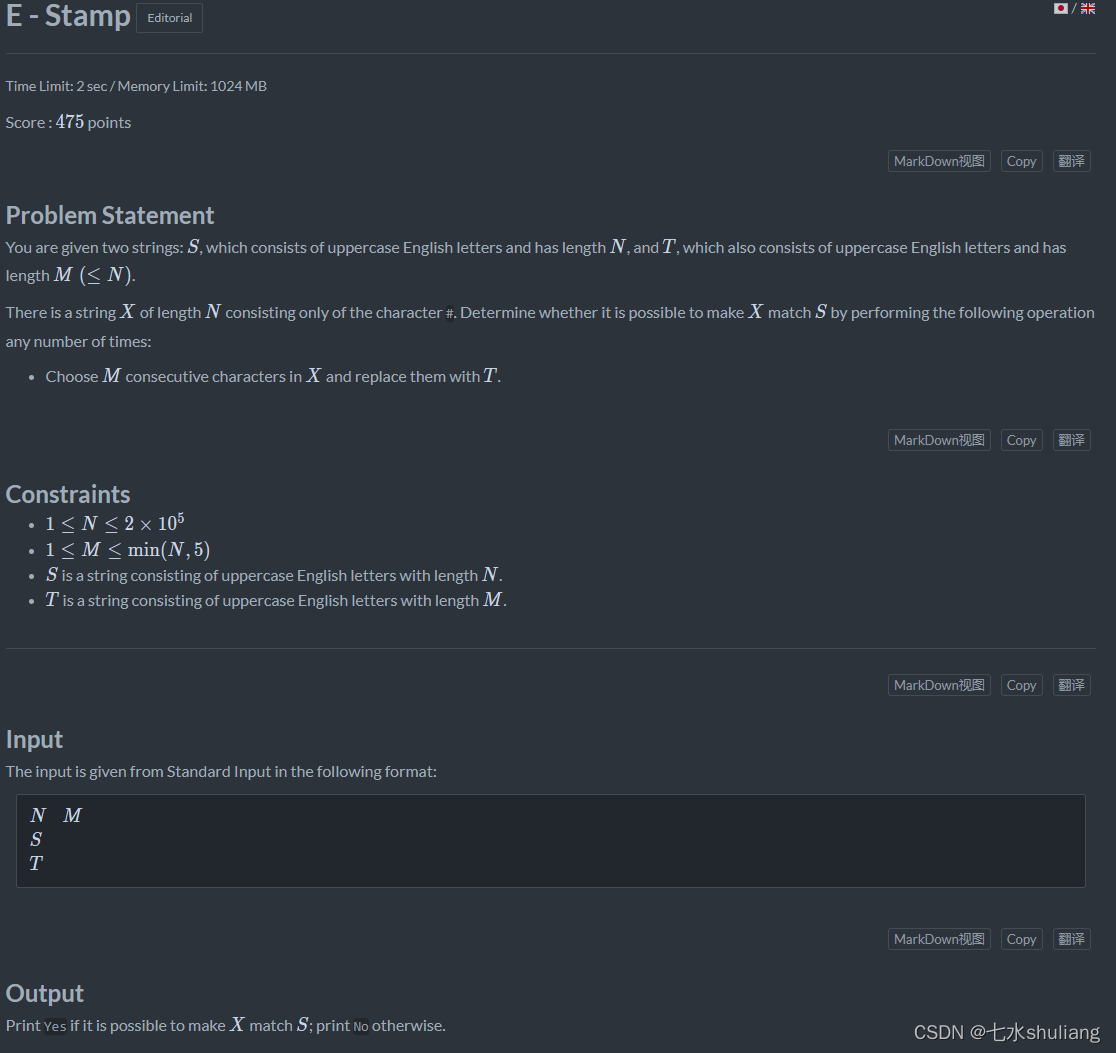
已知len(t)<len(s),问s可不可以由t覆盖拼接而来。即给长为len(s)的格子,通过无限盖地毯t的方式,铺满格子,且俯视图是s。
- 由看到m<=5,考虑dp。
- 令f[i][0~4]表示s[i]位置能不能匹配t[j]。那么,只有s[i]==s[j]时才能匹配,另外还要满足:
- 如果前一个位置可以匹配t[j-1],那么这里可以匹配t[j]
- 如果j=0,那么可以从这个位置新盖一块t。
- 如果前一个位置可以匹配t[-1],那这里可以匹配任何位置,盖完了再盖前边即可。
- 另外注意,地毯前后不能越界,即j<=i 且m-j<=n-i。
- 实现时可以空间优化。
- 注意方案必须每个位置都有匹配项,不能只判断f[-1][-1]。
3. 代码实现
def solve():
n, m = RI()
s, = RS()
t, = RS()
f = [0] * m
f[0] = s[0] == t[0]
for i in range(1, n):
if not sum(f):
return print('No')
g = [0]*m
for j in range(min(m, i + 1)):
if s[i] == t[j] and m - j <= n - i:
if j == 0 or f[m-1] or f[j-1]:
g[j] = 1
f = g
print(['No', 'Yes'][f[-1]])
def solve1():
"""
f[i][0~4]表示前缀匹配时,s[i]是否能用t[j]来匹配
"""
n, m = RI()
s, = RS()
t, = RS()
f = [[0] * m for _ in range(n)]
f[0][0] = s[0] == t[0]
for i in range(1, n):
if not sum(f[i - 1]):
return print('No')
for j in range(min(m, i + 1)):
if s[i] == t[j] and m - j <= n - i:
if j == 0:
f[i][j] = 1
elif f[i - 1][m - 1]:
f[i][j] = 1
elif f[i - 1][j - 1]:
f[i][j] = 1
print(['No', 'Yes'][f[-1][-1]])
F - Colored Ball
链接: F - Colored Ball
2. 思路分析
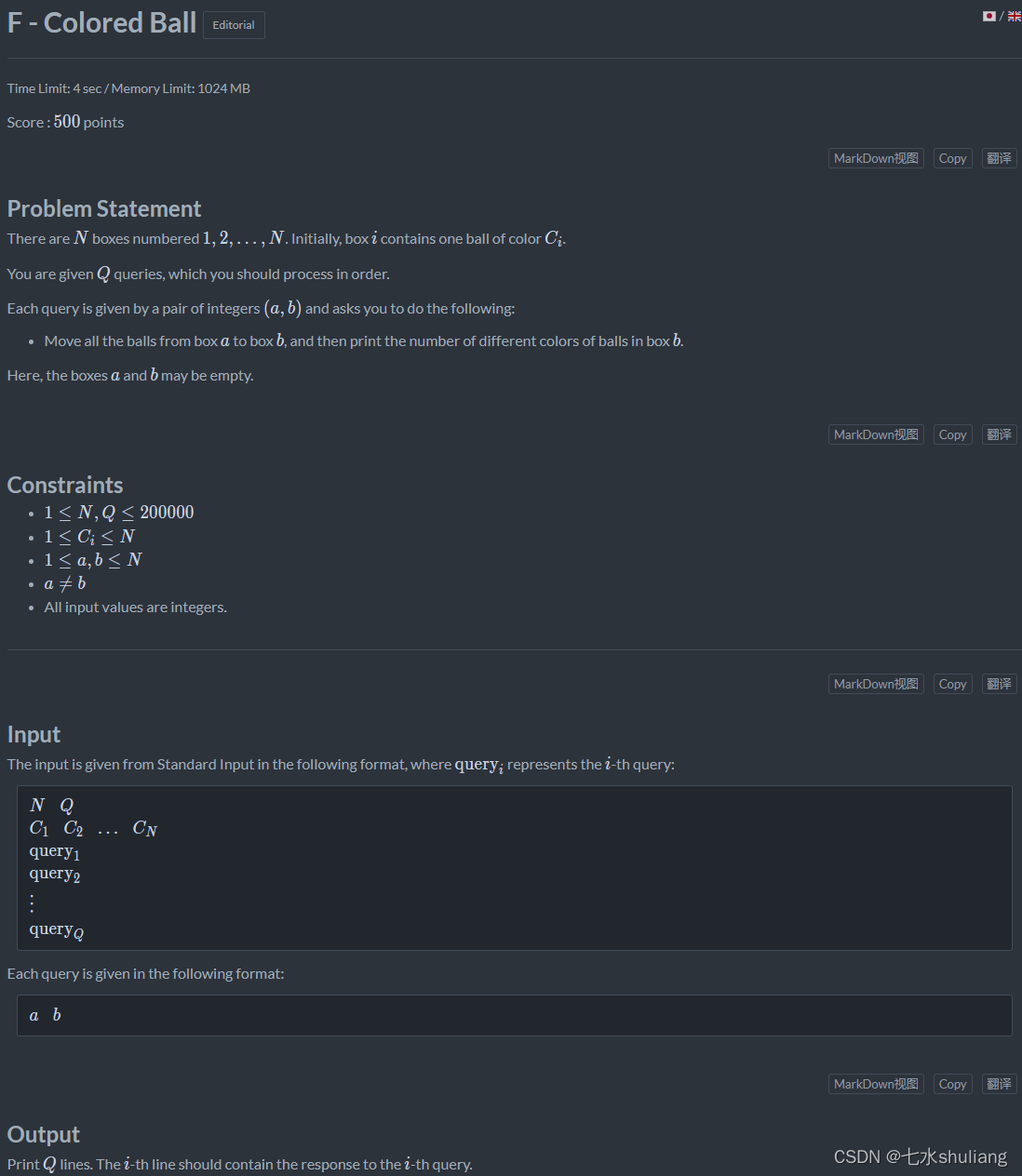
一开始每个盒子都有一种颜色的小球,q个操作,每次把a盒子所有球倒进b盒子,问b盒子每次的球数量。
- 语法题,启发式合并,把每次移动少的那边的盒子,然后整体给盒子动位置。
- 启发式合并均摊复杂度是O(nlgn)的。
- 有道类似的题,更难一些,用并查集F - BOX
3. 代码实现
# 379 ms
def solve():
n, q = RI()
c = [0] + RILST()
cc = [{v} for v in c]
for _ in range(q):
a, b = RI()
if len(cc[a]) > len(cc[b]):
cc[a], cc[b] = cc[b], cc[a]
cc[b] |= cc[a]
cc[a] = set()
print(len(cc[b]))
# 499 ms
def solve1():
n, q = RI()
c = [0] + RILST()
cc = [{v} for v in c]
for _ in range(q):
a, b = RI()
if len(cc[a]) < len(cc[b]):
for v in cc[a]:
cc[b].add(v)
cc[a] = set()
else:
for v in cc[b]:
cc[a].add(v)
cc[b] = cc[a]
cc[a] = set()
print(len(cc[b]))
六、参考链接
- 无


![【C++入门到精通】右值引用 | 完美转发 C++11 [ C++入门 ]](https://img-blog.csdnimg.cn/bb879b6a195246ec9f312e41c2be3af3.png)
![[黑马程序员SpringBoot2]——开发实用篇1](https://img-blog.csdnimg.cn/aea901f2eb224e418a9d11e4dab0b693.png)