🚀个人主页：为梦而生~ 关注我一起学习吧！
💡专栏：机器学习python实战 欢迎订阅！后面的内容会越来越有意思~
⭐内容说明：本专栏主要针对机器学习专栏的基础内容进行python的实现，部分基础知识不再讲解，有需要的可以点击专栏自取~
💡往期推荐（机器学习基础专栏）：
【机器学习基础】机器学习入门（1）
【机器学习基础】机器学习入门（2）
【机器学习基础】机器学习的基本术语
【机器学习基础】机器学习的模型评估（评估方法及性能度量原理及主要公式）
【机器学习基础】一元线性回归（适合初学者的保姆级文章）
【机器学习基础】多元线性回归（适合初学者的保姆级文章）
⭐本期内容：针对以上的一元和多元线性回归的梯度下降求解方法，进行代码展示

---

---

一元线性回归

• 设计思路：

首先，class LinearRegression(object):定义一个LinearRegression类，继承自object类。
在这个类中，首先def __init__(self):定义类的构造函数。

在构造函数中，初始化线性回归模型的参数self.__M、self.__theta0和self.__theta1，以及梯度下降中的步长（学习率）self.__alpha。

线性回归模型是要不断计算输出的，所以定义函数def predict(self, x)，用于预测给定输入x对应的输出。

同时线性回归的目的是通过迭代，不断的修改参数$\theta$，所以需要定义函数用来做这个工作，它是通过梯度下降的方法来求解的，所以def __cost_theta0(self, X, Y)和def __cost_theta1(self, X, Y)这两个方法用于计算代价函数关于参数${\theta }_0$和${\theta }_1$的偏导数。

下面，def train(self, features, target)把上面的每个步骤和到了一起，定义了一个训练方法train，用于通过梯度下降算法找到最优的模型参数${\theta }_0$和${\theta }_1$的，使得代价函数的平方误差最小。在训练过程中，通过迭代更新参数，并输出每次迭代后的参数值。

在while的每一次迭代中，通过更新参数self.__theta0和self.__theta1来逐渐最小化代价函数的平方误差。

if "0:o.5f".format(prevt0) == "0:o.5f".format(self.__theta0) and "0:o.5f".format(prevt1) == "0:o.5f".format(self.__theta1):判断是否达到收敛条件，即两次迭代的参数值没有改变，如果满足条件，则退出循环。

最后，输出最终得到的参数值。

• 总体代码实现：

定义LinearRegression的class

#!/usr/bin/env python3
# 这是一个Shebang，指定了此脚本要使用的解释器为python3。
import numpy

class LinearRegression(object):

    # Constructor. Initailize Constants.
    def __init__(self):
        super(LinearRegression, self).__init__()
        self.__M = 0
        self.__theta0 = 2
        self.__theta1 = 2

        # defining Alpha I.E length of steps in gradient descent Or learning Rate.
        self.__alpha = 0.01

    def predict(self,x):
        return (self.__theta0 + x * self.__theta1)
    
    # Cost Function fot theta0.
    def __cost_theta0(self,X,Y):
        
        sqrerror = 0.0
        for i in range(0,X.__len__()):
            sqrerror += (self.predict(X[i]) - Y[i])
        return (1/self.__M * sqrerror)
    
    # Cost Function fot theta1.
    def __cost_theta1(self,X,Y):
        sqrerror = 0.0
        for i in range(0,X.__len__()):
            sqrerror += (self.predict(X[i]) - Y[i]) * X[i]
        return (1/self.__M * sqrerror)


    # training Data :
    # Finding Best __theta0 and __theta1 for data such that the Squared  Error is Minimized.
    def train(self,features,target):
        
        # Validate Data
        if not features.__len__() == target.__len__():
            raise Exception("features and target should be of same length")

        # Initailize M with Size of X and Y
        self.__M = features.__len__()
        
        # gradient descent
        prevt0, prevt1 = self.__theta0 , self.__theta1
        
        while True:
            tmp0 = self.__theta0 - self.__alpha * (self.__cost_theta0(features,target))
            tmp1 = self.__theta1 - self.__alpha * (self.__cost_theta1(features,target))
           
            self.__theta0, self.__theta1 = tmp0, tmp1

            print("theta0(b) :", self.__theta0)
            print("theta1(m) :", self.__theta1)

            if "0:o.5f".format(prevt0) == "0:o.5f".format(self.__theta0) and "0:o.5f".format(prevt1) == "0:o.5f".format(self.__theta1):
                break
            
            prevt0, prevt1 = self.__theta0 , self.__theta1


        # Training Completed.
        # log __theta0 __theta1
        print("theta0(b) :", self.__theta0)
        print("theta1(m) :", self.__theta1)

样例测试

from LinearRegression_OneVariables import LinearRegression
import numpy as np

X = np.array([1,2,3,4,5,6,7,8,9,10])

# Y = 0 + 1X
Y = np.array([1,2,3,4,5,6,7,8,9,10])

modal = LinearRegression.LinearRegression()

modal.train(X,Y)

print(modal.predict(14))

---

多元线性回归

• 设计思路：

首先，将文件导入，打乱顺序并选择训练集。

data=pd.read_csv("c:\\windquality.csv")

data_array=data.values

#shuffling for train test spplit
np.random.shuffle(data_array)

train,test=data_array[:1200,:],data_array[1200:,:]
x_train=train[:,:-1]
x_test=test[:,:-1]
y_train=train[:,-1]
y_test=test[:,-1]

然后初始化参数，注意这里是多元的，所以有多个参数需要初始化。包括迭代次数和学习率

coef1=0
coef2=0
coef3=0
coef4=0
coef5=0
coef6=0
coef7=0
coef8=0
coef9=0
coef10=0
coef11=0
epoch=1000
alpha=.0001

然后使用梯度下降算法进行计算

总体代码实现：

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt


data=pd.read_csv("c:\\windquality.csv")

data_array=data.values

#shuffling for train test spplit
np.random.shuffle(data_array)

train,test=data_array[:1200,:],data_array[1200:,:]
x_train=train[:,:-1]
x_test=test[:,:-1]
y_train=train[:,-1]
y_test=test[:,-1]

coef1=0
coef2=0
coef3=0
coef4=0
coef5=0
coef6=0
coef7=0
coef8=0
coef9=0
coef10=0
coef11=0
epoch=1000
alpha=.0001
c=0
n=len(y_train)
for i in range(epoch):
    y_pred=((coef1*x_train[:,0])+(coef2*x_train[:,1])+(coef3*x_train[:,2])+(coef4*x_train[:,3])+
            (coef5*x_train[:,4])+(coef6*x_train[:,5])+(coef7*x_train[:,6])+(coef8*x_train[:,7])+
            (coef9*x_train[:,8])+(coef10*x_train[:,9])+(coef11*x_train[:,10])+c)
    
    
    #to predict drivative
    intercept=(-1/n)*sum(y_train-y_pred)
    dev1=(-1/n)*sum(x_train[:,0]*(y_train-y_pred))
    dev2=(-1/n)*sum(x_train[:,1]*(y_train-y_pred))
    dev3=(-1/n)*sum(x_train[:,2]*(y_train-y_pred))
    dev4=(-1/n)*sum(x_train[:,3]*(y_train-y_pred))
    dev5=(-1/n)*sum(x_train[:,4]*(y_train-y_pred))
    dev6=(-1/n)*sum(x_train[:,5]*(y_train-y_pred))
    dev7=(-1/n)*sum(x_train[:,6]*(y_train-y_pred))
    dev8=(-1/n)*sum(x_train[:,7]*(y_train-y_pred))
    dev9=(-1/n)*sum(x_train[:,8]*(y_train-y_pred))
    dev10=-1/n*sum(x_train[:,9]*(y_train-y_pred))
    dev11=-1/n*sum(x_train[:,10]*(y_train-y_pred))
    
    
    #line
    
    c=c-alpha*intercept
    coef1=coef1-alpha*dev1
    coef2=coef2-alpha*dev2
    coef3=coef3-alpha*dev3
    coef4=coef4-alpha*dev4
    coef5=coef5-alpha*dev5
    coef6=coef6-alpha*dev6
    coef7=coef7-alpha*dev7
    coef8=coef8-alpha*dev8
    coef9=coef9-alpha*dev9
    coef10=coef10-alpha*dev10
    coef11=coef11-alpha*dev11
    
    
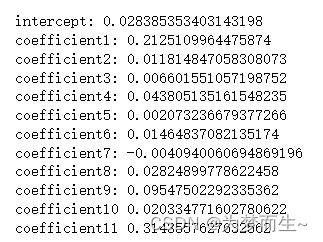
print("\nintercept:",c,"\ncoefficient1:",coef1,"\ncoefficient2:",coef2,"\ncoefficient3:",coef3,"\ncoefficient4:",coef4,
      "\ncoefficient5:",coef5,"\ncoefficient6:",coef6,"\ncoefficient7:",coef7,"\ncoefficient8:",coef8,"\ncoefficient9:",coef9,
      "\ncoefficient10",coef10,   "\ncoefficient11",coef11)
    
    

#Calculating the predicted values
predicted_values = []
for i in range(0,399):
    y_pred = ((coef1 * x_test[i,0]) + (coef2 * x_test[i,1]) + 
              (coef3 * x_test[i,2]) + (coef4 * x_test[i,3]) + 
              (coef5 * x_test[i,4]) + (coef6 * x_test[i,5]) + 
              (coef7 * x_test[i,6]) + (coef8 * x_test[i,7]) + 
              (coef9 * x_test[i,8]) + (coef10 * x_test[i,9]) + 
              (coef11 * x_test[i,10]) + intercept)
    predicted_values.append(y_pred)
    
for i in range(len(predicted_values)):
    print(predicted_values[i])