🌈欢迎来到Python专栏
🙋🏾‍♀️作者介绍：前PLA队员 目前是一名普通本科大三的软件工程专业学生
🌏IP坐标：湖北武汉
🍉 目前技术栈：C/C++、Linux系统编程、计算机网络、数据结构、Mysql、Python（目前在学）
🍇 博客介绍：通过分享学习过程，加深知识点的掌握，也希望通过平台能认识更多同僚，如果觉得文章有帮助，请您动动发财手点点赞，本人水平有限，有不足之处欢迎大家扶正~
🍓 最后送大家一句话共勉：知不足而奋进，望远山而前行。愿大家都能早日进大厂实现财富自由~
————————————————

1.参数解析

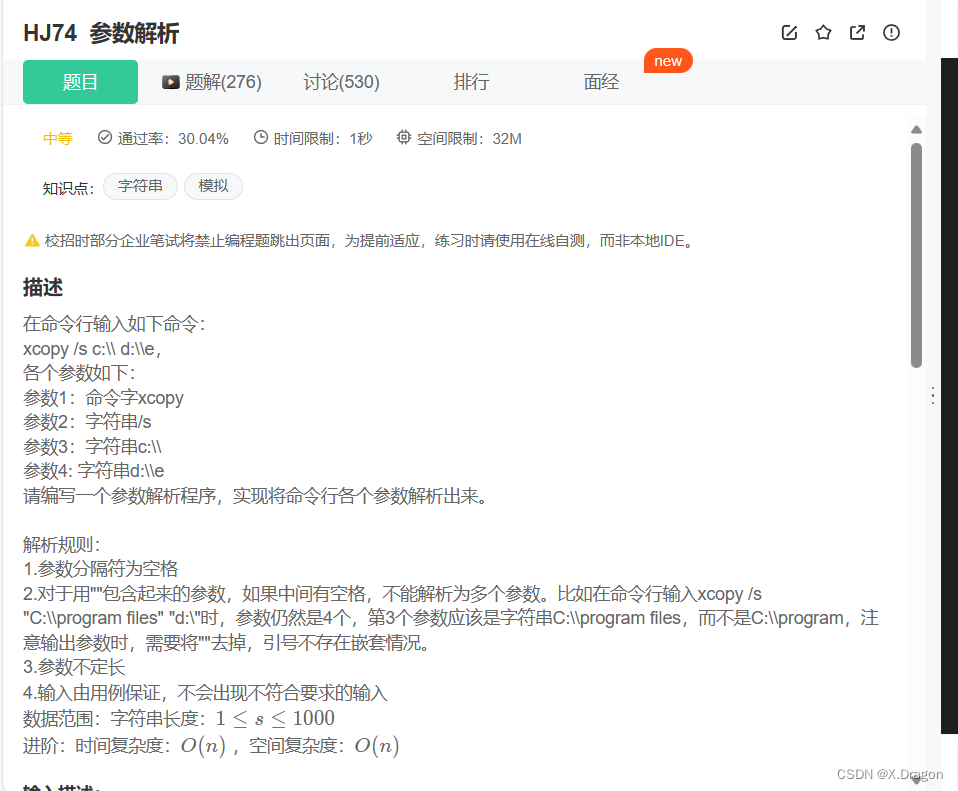
参数解析: [点击跳转](https://www.nowcoder.com/practice/668603dc307e4ef4bb07bcd0615ea677?tpId=37&&tqId=21
297&rp=1&ru=/activity/oj&qru=/ta/huawei/question-ranking)

【题目解析】：
本题考察string的运用
【解题思路】：
本题通过以空格和双引号为间隔，统计参数个数。对于双引号，通过添加flag，保证双引号中的空格被输
出。
【示例代码】

#include<iostream>
#include<string>
#include<vector>
using namespace std;
void cmdLineParse(const string &str)
{
string tmp = "";
vector<string> svec;
bool flag = false; //用于判断是否处于字符串的状态
for(int i=0; i<str.size(); ++i)
{
if(str[i] == '"') //判断是否是字符串的起始或者结束
{
flag = !flag; //说明处于了字符串的状态
}
else if(str[i]==' ' && !flag) //判断参数的分隔或者是否为字符串的内容
{
svec.push_back(tmp);
tmp = "";
}
else //正常的参数内容
{
tmp += str[i]; //xcopy
}
}
svec.push_back(tmp); //追加最后一个参数
cout<<svec.size()<<endl;
for(int i=0; i<svec.size(); ++i)
cout<<svec[i]<<endl;
}
int main()
{
string str;
while(getline(cin, str))
{
cmdLineParse(str);
}
return 0;
}

2.跳石板

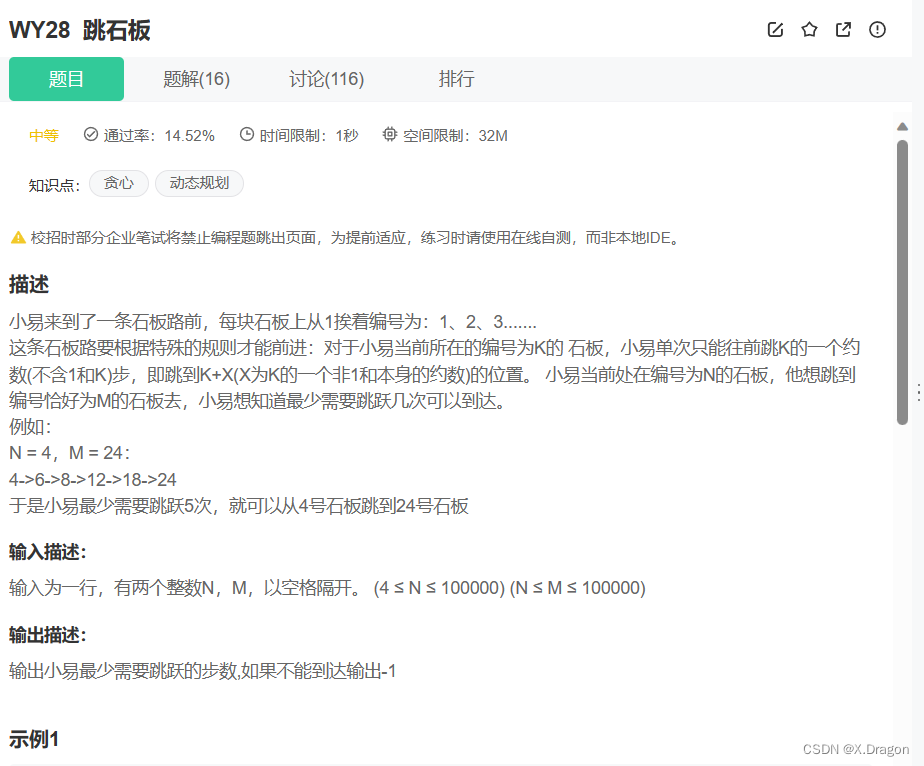
跳石板: 点击跳转

题解：
题目的意思是从N开始，最少需要累加几步可以变成指定的数字M，每次累加的值为当前值的一个约数。
【解题思路】：
将1 - M个石板看做一个结果数组stepNum，每个stepNum[i]储存着从起点到这一步最小的步数，其中0为不
能到达。 从起点开始对stepNum进行遍历，先求i的所有约数（即从stepNum[i]能走的步数），然后更新那
几个能到达的位置的最小步数。如果不能到达则更新为此时位置的最小步数 + 1，如果是能到达的就更新为
min（已记录的最小步数，此处的最小步数 + 1）），遍历一遍后得到结果。
【示例代码】

#include<iostream>
#include<vector>
#include<limits.h>
#include<math.h>
using namespace std;
void get_div_num(int v, vector<int>& a) {
    for (int i = 2; i <= sqrt(v); ++i) {
        if (v % i == 0) {
            a.push_back(i);
            if (v / i != i)
                a.push_back(v / i);
        }
    }
}
int Jump(int n, int m) {
    vector<int> step(m + 1, INT_MAX); //int_max表示不可达到
    step[n] = 0; //当前位置初始化
    for (int i = n; i < m; ++i) {
        if (step[i] == INT_MAX)
            continue;
        vector<int> a;
//获取i的约数，并保存
        get_div_num(i, a);
        for (int j = 0; j < a.size(); ++j) {
            if (a[j] + i <= m && step[a[j] + i] != INT_MAX) {
//需要挑选一个最小值
                step[a[j] + i] = step[a[j] + i] < step[i] + 1 ? step[a[j] + i] : step[i] + 1;
            } else if (a[j] + i <= m) {
                step[a[j] + i] = step[i] + 1;
            }
        }
    }
    return step[m] == INT_MAX ? -1 : step[m];
}
int main() {
    int n, m, min_step;
    while (cin >> n >> m) {
        min_step = Jump(n, m);
        cout << min_step << endl;
    }
    return 0;
}