M:
- intrinsic matrix
[ f x s c x 0 f y c y 0 0 1 ] \begin{bmatrix}f_x & s & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1\end{bmatrix} fx00sfy0cxcy1
(
c
x
,
c
y
)
(c_x, c_y)
(cx,cy): camera center in pixels
(
f
x
,
f
y
)
(f_x, f_y)
(fx,fy): focal length in pixels
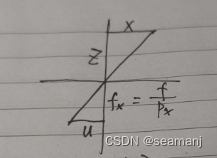
X
Z
=
u
f
x
\frac{X}{Z} = \frac{u}{f_x}
ZX=fxu
其中
f
x
=
f
p
x
f_x = \frac{f}{p_x}
fx=pxf,
f
f
f 是focal length in world unites (millimeters),
p
x
p_x
px像素宽度, 通过胶片宽度除以像素X方向的个数得到.
下面来看skew
s = f x t a n α s = f_x tan \alpha s=fxtanα
假设每
p
y
p_y
py在
p
x
p_x
px上面的偏移是
b
b
b
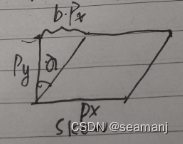
那么
t
a
n
α
=
b
p
x
p
y
tan \alpha = \frac{bp_x}{p_y}
tanα=pybpx
那么 [ f x s c x 0 f y c y 0 0 1 ] ∗ [ X Z Y Z 1 ] \begin{bmatrix}f_x & s & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1\end{bmatrix} *\begin{bmatrix} \frac{X}{Z} \\ \frac{Y}{Z} \\ 1 \end{bmatrix} fx00sfy0cxcy1 ∗ ZXZY1
第一行可得 f x ∗ X Z + s ∗ Y Z + c x = f x ∗ X Z + f x t a n α ∗ Y Z + c x f_x * \frac{X}{Z} +s * \frac{Y}{Z} + c_x = f_x * \frac{X}{Z} + f_x tan \alpha * \frac{Y}{Z} + c_x fx∗ZX+s∗ZY+cx=fx∗ZX+fxtanα∗ZY+cx
这里 f x t a n α ∗ Y Z f_x tan \alpha * \frac{Y}{Z} fxtanα∗ZY有两种理解方式, 第一种是通过 t a n α ∗ Y tan \alpha *Y tanα∗Y将在世界坐标系中将 Y Y Y转成 X X X方向的偏移 b X bX bX, 然后将这个偏移通过乘以 f x z \frac{f_x}{z} zfx转成x方向的像素偏移
第二种是 f x t a n α ∗ Y Z = f p x ∗ b p x p y ∗ Y Z = b f y ∗ Y Z f_x tan \alpha * \frac{Y}{Z} = \frac{f}{p_x}*\frac{bp_x}{p_y} * \frac{Y}{Z} = bf_y*\frac{Y}{Z} fxtanα∗ZY=pxf∗pybpx∗ZY=bfy∗ZY 先算在y方向有多少像素, 再乘以 b b b得到偏移
第二行注意如果有skew, 那么 f y f_y fy得用 f y c o s α \frac{f_y}{cos\alpha} cosαfy代替, 因为y轴变斜了, 相应也变长了
https://towardsdatascience.com/camera-calibration-fda5beb373c3
https://towardsdatascience.com/what-are-intrinsic-and-extrinsic-camera-parameters-in-computer-vision-7071b72fb8ec