目录
前言
一、读懂题目
二、思路分析
三、代码呈现
总结
前言
当我们需要实现队列的先进先出特性时，可以使用栈来模拟队列的行为。本文将介绍如何使用两个栈来实现队列，并给出具体的思路和代码实现。
一、读懂题目
题目：用两个栈实现一个队列。队列的声明如下，请实现它的两个函数 appendTail 和 deleteHead，分别完成在队列尾部插入结点和在队列头部删除结点的功能。
当我们需要利用栈来实现队列先进先出的特性时，考虑到单个栈对存入的一组数据push后再逐位pop取出，对应的序列和输入的顺序相反，那我们是否可以用两个栈，抽象类似于负负得正的手法，使得top位逐个取出得到的序列和插入时是相同的？
二、思路分析
首先基础类定义如下，我们只需要补充里面 appendTail 和 deleteHead 两函数的定义即可：
// 用两个栈实现队列
template<typename T>
class MyQueue
{
public:
void appendTail(const T& n);
T deleteHead();
private:
stack<T> st1;
stack<T> st2;
};为了便于表示和说明，设定一组数据 {a, b, c, d, e} 作为测试序列。
我们看到两个栈都可存储数据，那我们不妨先将数据全部存入st1中，那么根据栈先进后出的特性，两栈中数据的存储此时应该是这样的：
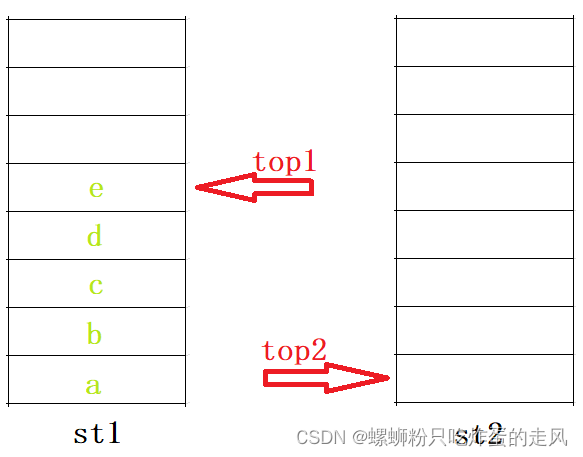
既然我们想到试试“负负得正”这种方法，那要是把st1中的元素再一 一取出放入st2中，是不是相当于把序列的顺序调转再调转，这样当我们不断取 st2.top() 时，最后按照取出的序列就是原来顺序的初始序列！
我们模拟一下这个过程：
1）对st1执行两次取首压入st2中：
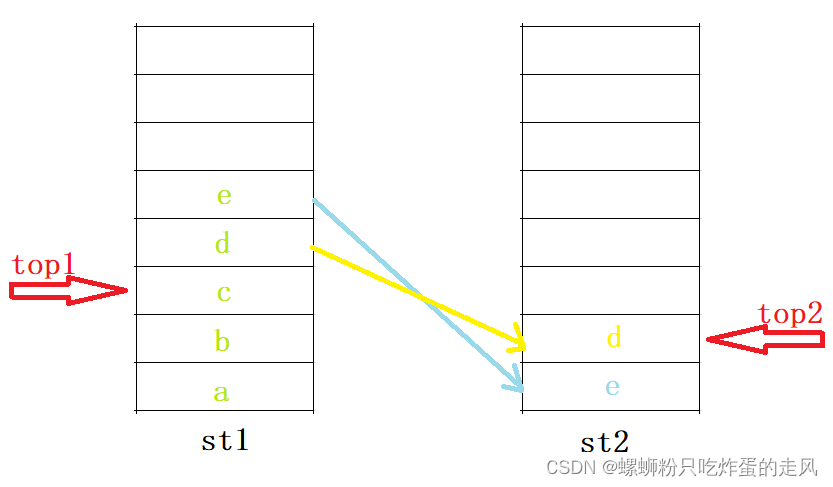
2）将剩余元素从st1中全部压入st2中，此时st1为空：
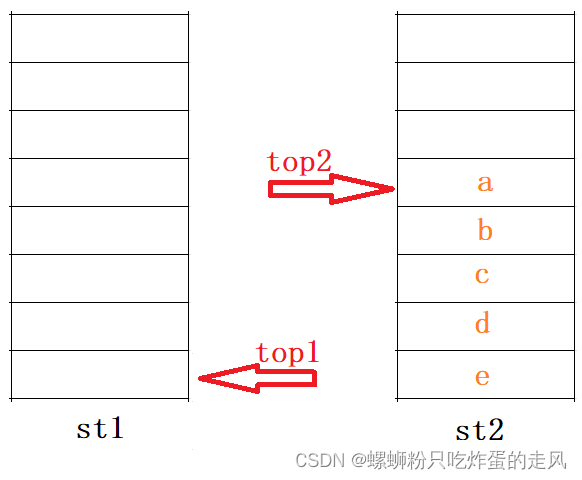
3）最后每当该模拟队列执行一次 front() 操作就返回 top2 所指向的值，每次 pop() 就从 st2 取出栈顶元素（前提是st1为空），直到 st2 栈为空：
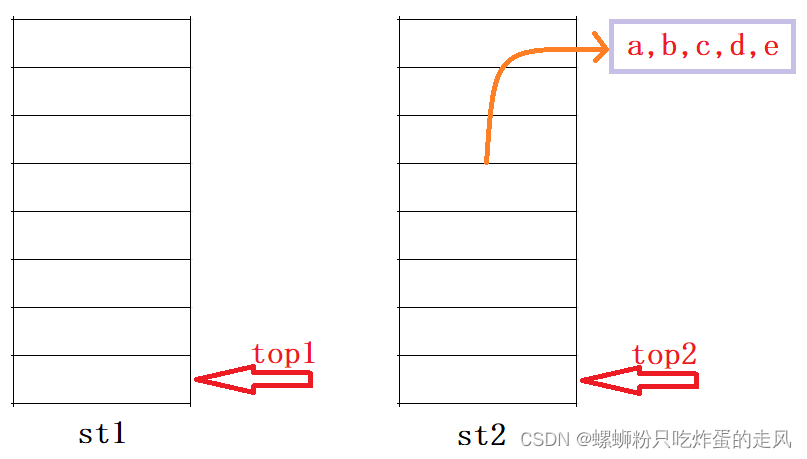
那如果在执行 front() 过程中，夹杂着新的push()指令，应该将新元素放入st1还是st2呢？如果st1不为空，要先将st1全部按照上面的规则移入st2后再插入还是先放入st1栈顶，再统一移入st2呢？
首先我们明确每个元素都需要经历“负负得正”的过程，所以首先新加元素肯定要先经过st1才能进入st2中。那是否需要st1及时清空呢？
我们不妨以 {a, b, c, d}, {e} 模拟两批次对模拟队列执行push()指令：
假定我们在每批操作结束就将该批的元素依次弹出并置入st2中，那么当需要输入上面第二组（即{e}）时，st1和st2的存储情况如下：
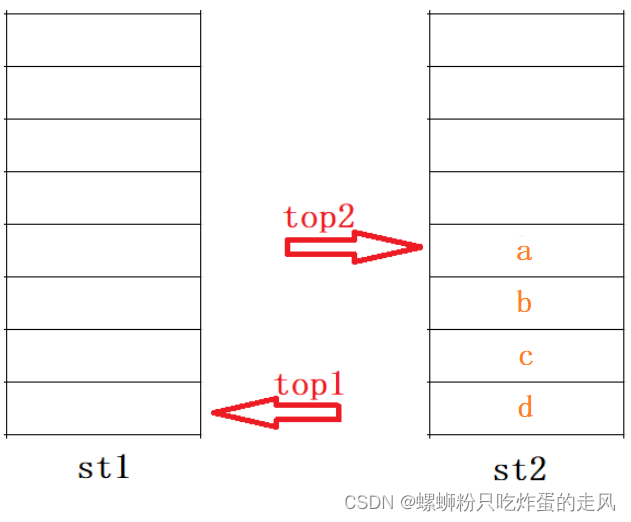
接下来该插入第二批数据了，但是实际功能调用过程中，不可能每次单批次插入操作之间是连续的，中间可能会有删除队列中已有元素的操作，所以我们不妨在两次 push() 指令中间加一句 pop_front() 指令，那么当接着执行一次pop_front() 指令时，对于st2而言应该将 a 元素剔除。同时我们注意到 a 元素正如我们所料位于st2的栈顶，当 st2.pop() 操作执行时，取出 a 元素，符合队列先进先出的特性。此时st1为空，st2顶部元素为b，如下图：
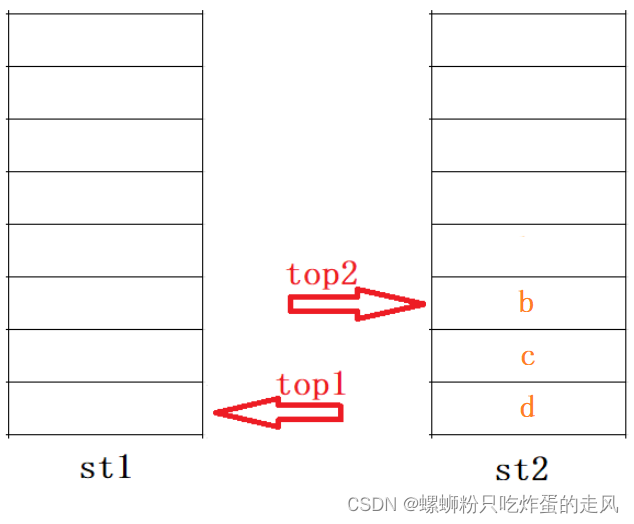
下一步我们进行第二批插入，将元素 e 执行 push() 操作时，显然 e 需要先进st1中，所以st1中此时不为空，元素ｅ即为st1栈顶元素：
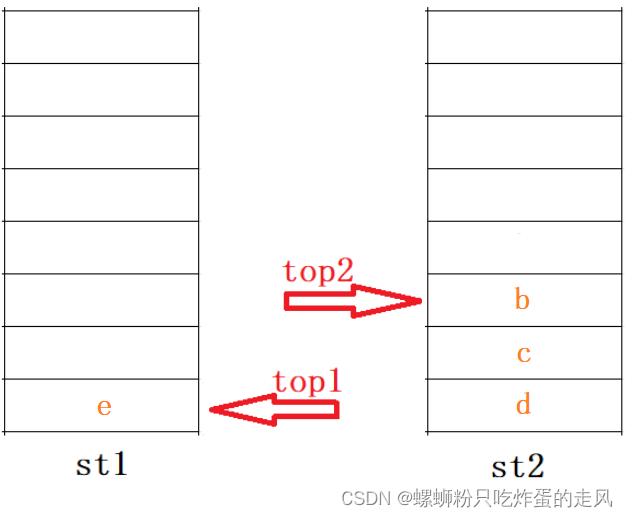
那么此时我们要不要把st1中的所有元素（这里仅有 e ）顺手植入st2中呢？
1）如果移入st2中：
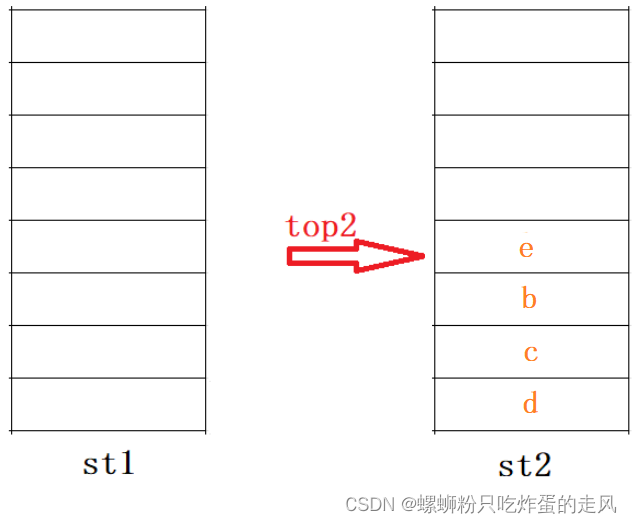
现在面临一个问题：如果我们一次性取出st2中的元素，亦或是仅取st2栈顶元素执行 st2.pop() 来获得理想的队列头，却发现得到的结果并不满足我们的设计需求，两轮输入的总序列为 {a, b, c, d, e} ，而取出序列为 {a, e, ... }，显然不符合先进先出的原则。
那是否意味着第二批的输入元素应该先保存在st1中，并非单批输入结束后就将其接着压入st2中，那为什么首批输入的数据就可以直接经st1后全部置入st2呢？
难道因为开始时候 st2 为空吗？那如果后续其他批次插入时，也遵循 st2 为空后再将 st1 中所有元素置于 st2 中，会不会发生这样的冲突？
不妨我们按照这样的设计思路进行测试：
首先给出部分功能的此思路代码：
1）清空 st1 容器功能代码
template<typename T>
void MyQueue<T>::appendOver()
{
if (st2.empty()) // 只有满足st2为空才清空st1
{
while (!st1.empty())
{
st2.push(st1.top());
st1.pop();
}
}
}2）模拟 front() , push() 和 pop() 的函数功能
template<typename T>
T& MyQueue<T>::front()
{
if (!st1.empty())
{
appendOver();
}
assert(!st2.empty());
return st2.top();
}
template<typename T>
void MyQueue<T>::appendTail(const T& n)
{
st1.push(n);
}
template<typename T>
T MyQueue<T>::deleteHead()
{
assert(!empty()); // 不能同时为空
if (st2.empty())
{
appendOver();
}
T tmp_poped = st2.top();
st2.pop();
return tmp_poped;
}3）实际测试代码
void test1()
{
MyQueue<int> mq;
// queue.push()模拟尾插
for (int i = 10; i > 0; i--)
{
mq.appendTail(i);
} // 1 2 3 4 5 6 7 8 9 10 右侧栈顶
// queue.front()模拟取首元素
// appendTail()--push()模拟入队列操作
// deleteHead()--pop()模拟删除队列首元素
mq.deleteHead(); // st1中：空 st2中：1 2 3 4 5 6 7 8 9 右侧栈顶
mq.appendTail(100); // st1中：100 st2中：1 2 3 4 5 6 7 8 9 右侧栈顶
// 由于st2不为空，st1中元素不发生迁移
// 经过上面两步 st1中：100 st2中：1 2 3 4 5 6 7 8 9
// 假设我们再进行一组类似操作
mq.deleteHead(); // st1中：100 st2中：1 2 3 4 5 6 7 8 右侧栈顶
mq.appendTail(55); // st1中：55 100 st2中：1 2 3 4 5 6 7 8 右侧栈顶
int val = mq.deleteHead(); // st1中：55 100 st2中：1 2 3 4 5 6 7 右侧栈顶
printf("val = %d\n", val); // 8
PopAndPrintMyQueue<int>(mq);
}按理来说结果应该和各行代码后面的理想推测相同，我们看看最后两行执行结果：
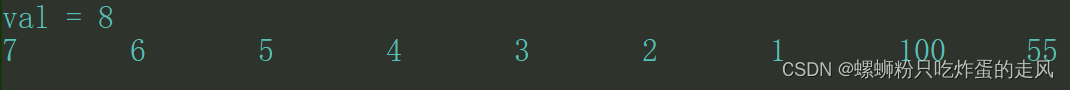可以看到和我们推测的结果完全一致，我们不仅在上面完成了一组插入删除后，额外执行了一组插入和删除操作，最后打印整个模拟队列中剩余元素时，呈现的结果和传入的顺序也相同，同样可以采用其他各种操作，统计每次取出的元素组成的序列是否满足先进先出的特性，结果终究是符合的。
三、代码呈现
下面直接给出代码：
// 用两个栈实现队列
template<typename T>
class MyQueue
{
public:
void appendTail(const T& n);
T deleteHead();
T& front();
bool empty();
private:
void appendOver(); // 将st1中元素的全部移入st2中 --- 前提：st2不为空
stack<T> st1;
stack<T> st2;
};
template<typename T>
void MyQueue<T>::appendTail(const T& n)
{
st1.push(n);
}
template<typename T>
void MyQueue<T>::appendOver()
{
if (st2.empty()) // 只有满足st2为空才清空st1
{
while (!st1.empty())
{
st2.push(st1.top());
st1.pop();
}
}
}
template<typename T>
bool MyQueue<T>::empty()
{
if (st1.empty() && st2.empty())
{
return true;
}
return false;
}
template<typename T>
T MyQueue<T>::deleteHead()
{
assert(!empty()); // 不能同时为空
if (st2.empty())
{
appendOver();
}
T tmp_poped = st2.top();
st2.pop();
return tmp_poped;
}
template<typename T>
T& MyQueue<T>::front()
{
if (st2.empty())
{
appendOver();
}
assert(!st2.empty());
return st2.top();
}
template<typename T>
void PopAndPrintMyQueue(MyQueue<T>& my_q)
{
while (!(my_q.empty()))
{
cout << my_q.front() << "\t";
my_q.deleteHead();
}
cout << endl;
}
void test1()
{
MyQueue<int> mq;
// queue.push()模拟尾插
for (int i = 10; i > 0; i--)
{
mq.appendTail(i);
} // 1 2 3 4 5 6 7 8 9 10 右侧栈顶
// queue.front()模拟取首元素
// appendTail()--push()模拟入队列操作
// deleteHead()--pop()模拟删除队列首元素
mq.deleteHead(); // st1中：空 st2中：1 2 3 4 5 6 7 8 9 右侧栈顶
mq.appendTail(100); // st1中：100 st2中：1 2 3 4 5 6 7 8 9 右侧栈顶
// 由于st2不为空，st1中元素不发生迁移
// 经过上面两步 st1中：100 st2中：1 2 3 4 5 6 7 8 9
// 假设我们再进行一组类似操作
mq.deleteHead(); // st1中：100 st2中：1 2 3 4 5 6 7 8 右侧栈顶
mq.appendTail(55); // st1中：55 100 st2中：1 2 3 4 5 6 7 8 右侧栈顶
int val = mq.deleteHead(); // st1中：55 100 st2中：1 2 3 4 5 6 7 右侧栈顶
printf("val = %d\n", val); // 8
PopAndPrintMyQueue<int>(mq);
}
值得注意的是，上面对重要功能的安全性检查中，下面两种写法其本质是相同的：
// 1.
if (st2.empty())
{
appendOver();
}
assert(!st2.empty());
// 2.
assert(!empty()); // 不能同时为空
if (st2.empty())
{
appendOver();
}总结
本文详细介绍了如何利用栈来实现队列的先进先出特性。通过使用两个栈，我们可以将插入的顺序和取出的顺序保持一致。文章讨论了具体的实现思路，并通过代码实例进行了测试。通过测试结果，我们验证了模拟队列的各种操作都满足先进先出的特性。这种使用栈实现队列的方法在实际应用中具有重要的意义。
