2019 年 1 月份管综初数真题
一、问题求解(本大题共 5 小题,每小题 3 分,共 45 分)下列每题给出 5 个选项中,只有一个是符合要求的,请在答题卡上将所选择的字母涂黑。
1、某车间计划 10 天完成一项任务,工作 3 天后因故停工 2 天。若要按原计划完成任务,则工作效率需要提高( )
A.20%
B.30%
C.40%
D.50%
E.60%
工程问题
设工作效率需要提高x,原工作效率为
1
10
\frac{1}{10}
101 ,根据题意,得
1
10
×
3
+
1
10
×
(
1
+
x
)
×
5
=
1
\frac{1}{10}×3+\frac{1}{10}×(1+x)×5=1
101×3+101×(1+x)×5=1,解得:x=40%
2、设函数
f
(
x
)
=
2
x
+
a
x
2
(
a
>
0
)
f(x)=2x+\frac{a}{x^2}(a>0)
f(x)=2x+x2a(a>0) 内
(
0
,
+
∞
)
(0,+∞)
(0,+∞)的最小值为
f
(
x
0
)
=
12
f(x_0)=12
f(x0)=12,则
x
0
x_0
x0=( )
A.5
B.4
C.3
D.2
E.1
f
(
x
)
=
2
x
+
a
x
2
=
x
+
x
+
a
x
2
≥
3
x
⋅
x
⋅
a
x
2
3
=
3
a
3
f(x)=2x+\frac{a}{x^2}=x+x+\frac{a}{x^2}≥3\sqrt[3]{x·x·\frac{a}{x^2}}=3\sqrt[3]{a}
f(x)=2x+x2a=x+x+x2a≥33x⋅x⋅x2a=33a
故当
x
=
x
=
a
x
2
x=x=\frac{a}{x^2}
x=x=x2a时,f(x)取得最小值,即有
{
x
0
=
a
x
0
2
f
(
x
0
)
=
3
a
3
=
12
\begin{cases} x_0=\frac{a}{x_0^2} \\ f(x_0)=3\sqrt[3]{a}=12 \end{cases}
{x0=x02af(x0)=33a=12
解得:
x
0
=
4
x_0=4
x0=4
3、某影城统计了一季度的观众人数,如图,则一季度的男女观众人数之比为( )
A.3:4
B.5:6
C.12:13
D.13:12
E.4:3

【解析】母题99·图像图表问题+母题92·比例问题
观察图像,可知一季度男观众的总人数为5+4+3=12(万人),女观众的总人数为6+3+4=13(万人)
则一季度的男、女观众人数之比为12∶13
4、设实数 a, b 满足 ab = 6 , ∣ a + b ∣ + ∣ a − b ∣ = 6 |a+b|+|a-b|=6 ∣a+b∣+∣a−b∣=6 ,则 a 2 + b 2 a^2+b^2 a2+b2 =( )
A.10
B.11
C.12
D.13
E.14
【解析】母题13·绝对值方程和绝对值不等式
由题意知目的是求
a
2
+
b
2
a^2+b^2
a2+b2的值,故a,b的大小关系不影响结果。
又由ab=6知,a,b同号。不妨设a>b>0,则已知条件可转化为。解得a=3,b=2。
满足所给条件,可得
a
2
+
b
2
=
13
a^2+b^2=13
a2+b2=13。故应选(D).
【快速得分法】特殊值法,易观察可令a=3,b=2。
5、设圆C与圆
(
x
−
5
)
2
+
y
2
=
2
(x-5)^2+y^2=2
(x−5)2+y2=2关于
y
=
2
x
y=2x
y=2x 对称,则圆 C 方程为( )
A.
(
x
−
3
)
2
+
(
y
−
4
)
2
=
2
(x-3)^2+(y-4)^2=2
(x−3)2+(y−4)2=2
B.
(
x
+
4
)
2
+
(
y
−
3
)
2
=
2
(x+4)^2+(y-3)^2=2
(x+4)2+(y−3)2=2
C.
(
x
−
3
)
2
+
(
y
+
4
)
2
=
2
(x-3)^2+(y+4)^2=2
(x−3)2+(y+4)2=2
D.
(
x
+
3
)
2
+
(
y
−
3
)
2
=
2
(x+3)^2+(y-3)^2=2
(x+3)2+(y−3)2=2
E.
(
x
+
3
)
2
+
(
y
−
4
)
2
=
2
(x+3)^2+(y-4)^2=2
(x+3)2+(y−4)2=2
6、将一批树苗种在一个正方形花园边上,四角都种,如果每隔 3 米种一棵,那么剩下 10棵树苗;如果每隔 2 米种一棵,那么恰好种满正方形的 3 条边,则这批树苗有()棵。
A.54
B.60
C.70
D.82
E.94
7、在分别标记 1,2,3,4,5,6 的 6 张卡片,甲抽取一张,乙从余下的卡片中再抽取 2 张,乙的卡片数字之和大于甲的卡片数字的概率为()
A.
11
60
\frac{11}{60}
6011
B.
13
60
\frac{13}{60}
6013
C.
43
60
\frac{43}{60}
6043
D.
47
60
\frac{47}{60}
6047
E.
49
60
\frac{49}{60}
6049
8、10 名同学的语文和数学成绩如表
| 语文成绩 | 90 | 92 | 94 | 88 | 86 | 95 | 87 | 89 | 91 | 93 |
|---|---|---|---|---|---|---|---|---|---|---|
| 数学成绩 | 94 | 88 | 96 | 93 | 90 | 85 | 84 | 80 | 82 | 98 |
语文和数学成绩的均值分别为
E
1
E_1
E1 和
E
2
E_2
E2 ,标准差分别为
σ
1
σ_1
σ1和
σ
2
σ_2
σ2,则
A.
E
1
>
E
2
,
σ
1
>
σ
2
E_1>E_2,σ_1>σ_2
E1>E2,σ1>σ2
B.
E
1
>
E
2
,
σ
1
<
σ
2
E_1>E_2,σ_1<σ_2
E1>E2,σ1<σ2
C.
E
1
>
E
2
,
σ
1
=
σ
2
E_1>E_2,σ_1=σ_2
E1>E2,σ1=σ2
D.
E
1
<
E
2
,
σ
1
>
σ
2
E_1<E_2,σ_1>σ_2
E1<E2,σ1>σ2
E.
E
1
<
E
2
,
σ
1
<
σ
2
E_1<E_2,σ_1<σ_2
E1<E2,σ1<σ2
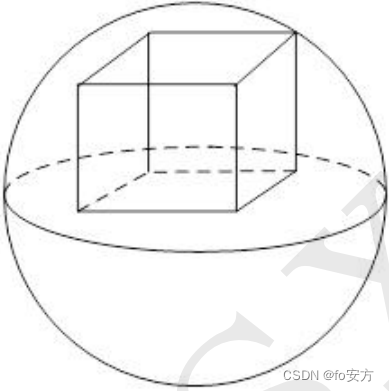
9、如图,正方体位于半径为 3 的球内,且一面位于球的大圆上,则正方体表面积最大为()
A.12
B.18
C.24
D.30
E.36
10、某中学的 5 个学科各推荐 2 名教师作为支教候选人,若从中选出来自不同学科的 2 人参加支教工作,则不同的选派方式有( )种
A. 20
B. 24
C. 30
D. 40
E. 45
11、某单位要铺设草坪,若甲、乙两公司合作需 6 天完成,工时费共 2.4 万元。若甲公司单独做 4 天后由乙公司接着做 9 天完成,工时费共计 2.35 万元。若由甲公司单独完成该项目,则工时费共计()万元
A.2.25
B.2.35
C.2.4
D.2.45
E.2.5
12、如图,六边形 ABCDEF 是平面与棱长为 2 的正方体所截得到的,若 A,B,D,E 分别为相应棱的中点,则六边形 ABCDEF 的面积为()
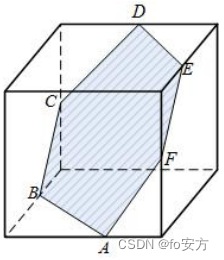
A.
3
2
\sqrt{3\over2}
23
B.
3
\sqrt{3}
3
C.
2
3
2\sqrt{3}
23
D.
3
3
3\sqrt{3}
33
E.
4
3
4\sqrt{3}
43
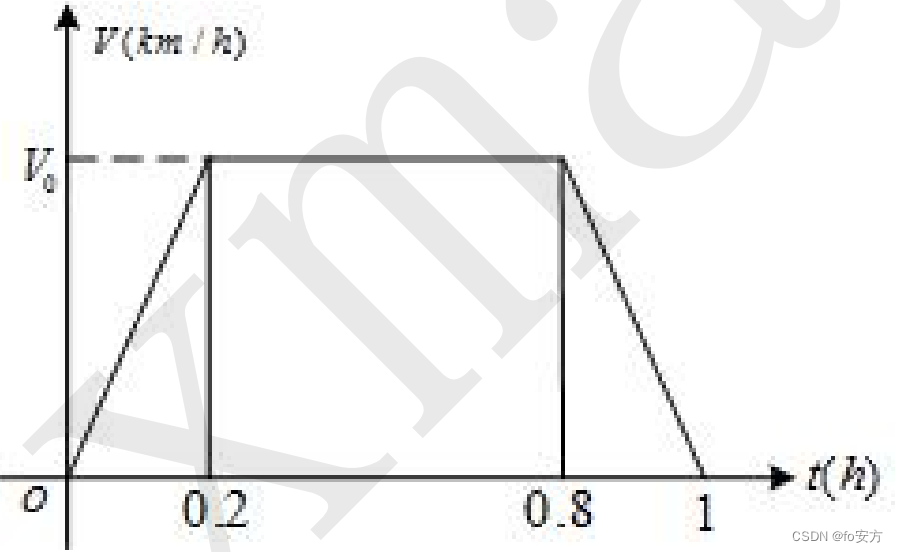
13、货车行驶 72km 用时 1 小时,速度V 与行驶时间t 的关系如图所示,则
V
o
=
V_o=
Vo=
A.72
B.80
C.90
D.85
E.100
14、在三角形 ABC 中, AB =4, AC =6, BC =8 ,D 为BC 的中点,则 AD =( )
A.
11
\sqrt{11}
11
B.
10
\sqrt{10}
10
C.3
D.
2
2
2\sqrt{2}
22
E.
7
\sqrt{7}
7
15、设数列{
a
n
{a_n}
an}满足
a
1
=
0
,
a
n
+
1
−
2
a
n
=
1
a_1=0,a_{n+1}-2a_n=1
a1=0,an+1−2an=1,则
a
100
=
a_{100}=
a100=()
A.
2
99
−
1
2^{99}-1
299−1
B.
2
99
2^{99}
299
C.
2
99
+
1
2^{99}+1
299+1
D.
2
100
−
1
2^{100}-1
2100−1
E.
2
100
+
1
2^{100}+1
2100+1
二.条件充分性判断:第 16-25 小题,每小题 3 分,共 30 分。
要求判断每题给出的条件(1)和(2)能否充分支持题干所陈述的结论 A、B、C、D、E 五个选项为判断结果,请选择一项符合试题要求的判断,请在答题卡上将所选的字母涂黑。
(A) 条件(1)充分,但条件(2)不充分
(B) 条件(2)充分,但条件(1)不充分
(C) 条件(1)和(2)都不充分,但联合起来充分
(D) 条件(1)充分,条件(2)也充分
(E) 条件(1)不充分,条件(2)也不充分,联合起来仍不充分
16、甲、乙、丙三人各自拥有不超过 10 本图书,甲再购入 2 本图书后,他们拥有的图书量构成等比数列,则能确定甲拥有图书的数量
(1) 已知乙拥有的图书数量
(2) 已知丙拥有的图书数量
17、有甲乙两袋奖券,获奖率分别为 p 和q ,某人从两袋中各随机抽取 1 张奖券,则此人获奖的概率不小于 3 2 \frac{3}{2} 23
(1) 已经 p + q = 1 p + q = 1 p+q=1
(2) 已知 p q = 1 4 pq=\frac{1}{4} pq=41
18、直线 y = k x y =kx y=kx 与圆 x 2 + y 2 − 4 x + 3 = 0 x^{2}+ y^2−4x+3 =0 x2+y2−4x+3=0 有两个交点
(1) − 3 3 < k < 0 -{\sqrt{3}\over3}<k<0 −33<k<0
(2) 0 < k < 2 2 0<k<{\sqrt{2}\over2} 0<k<22
19、能确定小明年龄
(1)小明年龄是完全平方数
(2)20年后小明年龄是完全平方数
20、关于 x 的方程 x 2 + a x + b = 1 x^2+ax+b=1 x2+ax+b=1有实根
(1) a +b =0
(2) a −b =0
21、如图,已知正方形 ABCD 面积,O 为 BC 上一点,P 为 AO 的中点,Q 为 DO 上一点,则能确定三角形 PQD 的面积。
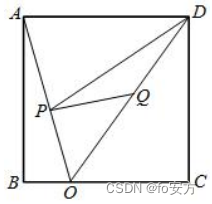
(1)O 为 BC 的三等分点
(2)Q 为 DO 的三等分点
22、设 n 为正整数,则能确定n 除以 5 的余数
(1) 已知 n 除以 2 的余数
(2) 已知n 除以 3 的余数
23、某校理学院五个系每年录取人数如下表:
| 系数 | 数学系 | 物理系 | 化学系 | 生物系 | 地学系 |
|---|---|---|---|---|---|
| 录取人数 | 60 | 120 | 90 | 60 | 30 |
今年与去年相比,物理系平均分没交,则理学院录取平均分升高了。
(1) 数学系录取平均分升高了 3 分,生物系录取平均分降低了 2 分
(2) 化学系录取平均分升高了 1 分,地学系录取平均分降低了 4 分
24、设三角区域D由直线 x + 8 y − 56 = 0 , x − 6 y + 42 = 0 x+8y-56=0,x-6y+42=0 x+8y−56=0,x−6y+42=0与 k x − y + 8 − 6 k = 0 ( k < 0 ) kx-y+8-6k=0(k<0) kx−y+8−6k=0(k<0)围成,则对任意的 ( x , y ) (x,y) (x,y), l g ( x 2 + y 2 ) ≤ 2 lg(x^2+y^2)≤2 lg(x2+y2)≤2
(1)
k
∈
(
−
∞
,
−
1
]
k∈(-∞,-1]
k∈(−∞,−1]
(2)
k
∈
[
−
1
,
−
1
8
)
k∈[-1,-{1\over8})
k∈[−1,−81)
25、设数列{
a
n
a_n
an}的前n项和为
S
n
S_n
Sn,则{
a
n
a_n
an}等差
(1)
S
n
=
n
2
+
2
n
,
n
=
1
,
2
,
3
S_n=n^2+2n,n=1,2,3
Sn=n2+2n,n=1,2,3
(2)
S
n
=
n
+
2
n
+
1
,
n
=
1
,
2
,
3
S_n=n^+2n+1,n=1,2,3
Sn=n+2n+1,n=1,2,3
2019年1月管理类联考数学参考答案
1-5 CBCDE
6-10 DDBED
11-15 EDCBA
16-20 CDACC
21-25 BECAA