报名明年4月蓝桥杯软件赛的同学们,如果你是大一零基础,目前懵懂中,不知该怎么办,可以看看本博客系列:备赛20周合集
20周的完整安排请点击:20周计划
每周发1个博客,共20周(读者可以按自己的进度选“正常”和“快进”两种计划)。
每周3次集中答疑,周三、周五、周日晚上,在QQ群上答疑:

文章目录
- 1. 数组的应用--高精度
- 1.1 Java和Python计算大数
- 1.2 C/C++高精度计算大数
- 1.2.1 高精度加法
- 1.2.2 高精度减法
- 1.2.3 高精度乘法
- 1.2.4 高精度除法
- 2. 队列
- 2.1 手写队列
- 2.1.1 C/C++手写队列
- 2.1.2 Java手写队列
- 2.1.3 Python手写队列
- 2.2 C++ STL队列queue
- 2.3 Java队列Queue
- 2.4 Python队列Queue和deque
- 2.5 例题
- 2.5.1 C/C++代码
- 2.5.2 Java代码
- 2.5.3 Python
- 3. 习题
第 6周: 高精度、队列
1. 数组的应用–高精度
高精度算法就是大数的计算方法。超过64位的大数计算,Java和Python都能直接算,而C++不能直接算,需要用数组来模拟大数的存储。
竞赛中常常用到很大的数组。强烈建议不要用动态分配,因为动态分配需要多写代码而且容易出错。定义为全局静态数组即可,而且不需要初始化为0,因为全局变量在编译时会自动初始化为全0。
#include <bits/stdc++.h>
using namespace std;
int a[10000000]; //定义一个很大的全局数组。自动初始化为0,不需要写成int a[10000000]={0};
int main(){
cout << a[0]; //输出0
return 0;
}
大数组不能定义在函数内部,这样做会导致栈溢出。因为局部变量是函数用到时才分配,大小不能超过栈,而栈不会很大。
这样写是错的:
#include <bits/stdc++.h>
using namespace std;
int main(){
int a[10000000]={0}; //这样写是错的,大数组不能定义在函数内部
cout << a[0]; //出错
return 0;
}
另外,注意全局变量和局部变量的初值。全局变量如果没有赋值,在编译时被自动初始化为0。在函数内部定义的局部变量,若需要初值为0,一定要初始化为0,否则可能为莫名其妙的值。
#include <bits/stdc++.h>
using namespace std;
int a; //全局变量自动初始化为0
int c = 999; //赋值为999
int main(){
int b;
cout << a <<endl; //输出0
cout << c <<endl; //输出999
cout << b <<endl; //由于b没有初始化,这里输出莫名奇妙的值
return 0;
}
1.1 Java和Python计算大数
Java和Python计算大数,理论上可以计算“无限大”的数,只要不超内存。
用下面的简单题说明Java和Python的大数计算。
【题目描述】 大数计算:输入两行表示两个整数。分别计算加、减、乘、除,分5行输出和、差、积、商、余数。
(1)Java代码。注意负数的计算,负数的加减乘都没问题,但是除法可能出错。
import java.math.BigInteger;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc=new Scanner(System.in);
BigInteger a,b;
a=sc.nextBigInteger();
b=sc.nextBigInteger();
System.out.println(a.add(b));
System.out.println(a.subtract(b));
System.out.println(a.multiply(b));
System.out.println(a.divide(b));
System.out.println(a.mod(b)); //注意:如果b是负数,这里可能报错
}
}
(2)Python代码。注意负数的计算,加减乘都没问题,但是除法的结果可能比较奇怪。
a=int(input())
b=int(input())
print(a+b)
print(a-b)
print(a*b)
print(a // b) #注意:如果a或b是负数,除法的结果可能比较怪,例如123//(-10)得-13
print(a % b) #注意:如果a或b是负数,求余的结果可能比较怪,例如123%(-10) 得-7
1.2 C/C++高精度计算大数
C++能表示的最大整数是64位的long long,如果需要计算更大的数,需要使用“高精度”。对于加减乘除四种计算,模拟每一位的计算,并处理进位或借位。
(1)数字的读取和存储。因为整数a和b太大,无法直接赋值给C++的变量,不能按数字读入,只能按字符读入。大数a用字符串string读入,一个字符存一位数字。注意存储的顺序,读入的时候,数字的左边是高位,右边是低位,即a[0]是最高位,a[n-1]是最低位;但是计算时习惯用a[0]表示最低位,a[n-1]表示最高位,所以需要把输入的字符串倒过来。
(2)加法和减法。简单地模拟即可。
(3)乘法。模拟小学竖式乘法操作,例如34×67,计算过程:

计算结果用int a[]存储,首先算出a[0]=4×7=28,a[1]=3×7+4×6=21+24,a[2]=3×6=18,然后处理进位,得到乘积2278。
(4)除法。直接做除法有点麻烦,简单一点的方法是利用减法。例如a除以b,转化为a连续减去b,减了多少次就是商,最后不够减的是余数。
1.2.1 高精度加法
链接:大整数加法
把输入的数字存到字符串中,然后在add()中把字符转成数字,做完加法后再转回字符。
#include<bits/stdc++.h>
using namespace std;
int na[1005],nb[1005]; //加数和被加数
string add(string a,string b){
int lena=a.size(),lenb=b.size();
for(int i=0;i<lena;i++)
na[lena-1-i] = a[i]-'0'; //把字符转成数字,然后翻转,使na[0]是最低位
for(int i=0;i<lenb;i++)
nb[lenb-1-i] = b[i]-'0';
int lmax = lena>lenb ? lena : lenb;
for(int i=0;i<lmax;i++) {
na[i] += nb[i];
na[i+1] += na[i]/10; //处理进位
na[i]%=10;
}
if(na[lmax]) lmax++; //若最高位相加后也有进位,数字长度加1
string ans;
for(int i=lmax-1;i>=0;i--) //把数字转成字符,然后翻转
ans += na[i]+'0';
return ans;
}
int main(){
string a,b;
cin >> a >> b;
cout << add(a,b);
return 0;
}
1.2.2 高精度减法
链接:大整数减法
#include<bits/stdc++.h>
using namespace std;
int na[1005],nb[1005]; //被减数和减数
string sub(string a,string b){
if(a == b) return "0"; //特判一下是否两数字相等
bool neg = 0; //标记是否为负数
if(a.size() < b.size() || a.size() == b.size() && a < b)
swap(a, b), neg = 1; //让a大于b
int lena=a.size(),lenb=b.size();
for(int i=0;i<lena;i++) //把字符转成数字,然后翻转,使na[0]是最低位
na[lena-1-i]=a[i]-'0';
for(int i=0;i<lenb;i++)
nb[lenb-1-i]=b[i]-'0';
int lmax = lena;
for(int i=0;i<lmax;i++){
na[i] -= nb[i];
if(na[i]<0){ //处理借位
na[i]+=10;
na[i+1]--;
}
}
while(!na[--lmax] && lmax>0) //找到首位为0的位置
; //什么都不做
lmax++;
string ans;
for(int i=lmax-1;i>=0;i--) //把数字转成字符,然后翻转
ans += na[i]+'0';
if(neg) ans = "-" + ans; //查询一下是否为负数
return ans;
}
int main(){
string a,b;
cin>>a>>b;
cout<<sub(a,b);
return 0;
}
1.2.3 高精度乘法
链接:大整数乘法
#include<bits/stdc++.h>
using namespace std;
int na[1005], nb[1005], nc[1000005];
string mul(string a,string b){
if(a=="0"||b=="0") return "0";
int lena=a.size(),lenb=b.size();
for(int i=0;i<lena;i++)
na[lena-i]=a[i]-'0';
for(int i=0;i<lenb;i++)
nb[lenb-i]=b[i]-'0';
for(int i=1;i<=lena;i++)
for(int j=1;j<=lenb;j++)
nc[i+j-1] += na[i]*nb[j];
for(int i=1;i<=lena+lenb;i++)
nc[i+1]+=nc[i]/10,nc[i]%=10;
string ans;
if(nc[lena+lenb]) ans += nc[lena+lenb]+'0';
for(int i=lena+lenb-1;i>=1;i--) ans += nc[i]+'0';
return ans;
}
int main(){
string a,b;
cin>>a>>b;
cout<<mul(a,b);
return 0;
}
1.2.4 高精度除法
链接:大整数除法
#include<bits/stdc++.h>
using namespace std;
string sub(string a,string b){//模拟大整数减法
string res;
int n=a.size(),m=b.size(),i,by=1;
reverse(a.begin(),a.end());
reverse(b.begin(),b.end());
for(i=0;i<m;++i){
int t=a[i]-b[i]+9+by;
res+=t%10+'0';
by=t/10;
}
for(;i<n;++i){
int t=a[i]-'0'+9+by;
res+=t%10+'0';
by=t/10;
}
//消去前缀零
while(res[--i]=='0'&&i>0);
res=res.substr(0,i+1);
reverse(res.begin(),res.end());
return res;
}
int main(){
string s1,s2,res,ans;
cin>>s1>>s2;
bool h=false;
int n=s1.size(),m=s2.size(),t;
//查找被除数末端非零位
int f=n-1;
while(s1[f]=='0')f--;
//模拟除法
for(int i=0;i<n;++i){//遍历被除数
ans+=s1[i];
t=0;
while(ans.size()>m||ans.size()==m&&ans>=s2){//具体操作
ans=sub(ans,s2);//用减法模拟除法
t++;
}
if(t||h){//等待商的首位
h=true;
res+=t+'0';
}
if(ans.empty()&&i>=f){//处理后缀零
while(++i<n)res+='0';
}
}
if(res.empty())res+='0';//余数为零
if(ans.empty())ans+='0';//商为零
cout<<res<<endl<<ans;
return 0;
}
2. 队列
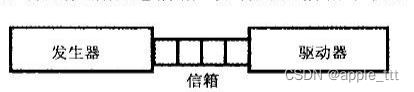
队列中的数据存取方式是“先进先出”,只能往队尾插入数据、从队头移出数据。队列的原型在生活中很常见,例如食堂打饭的队伍,先到先服务,不能插队。
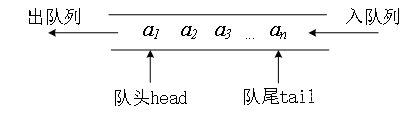
下图是队列的原理,队头head指向队列中的第一个元素
a
1
a_1
a1,队尾tail指向队尾最后一个元素
a
n
a_n
an。元素只能从队头方向出去,元素只能从队尾进入队列。
2.1 手写队列
2.1.1 C/C++手写队列
队列的代码很容易实现。如果使用环境简单,最简单的手写队列代码用数组实现。
const int N = 10000; //定义队列容量,确保够用
int que[N]; //队列,用数组模拟
int head = 0; //head始终指向队头。que[head]是队头。开始时队列为空,head = 0
int tail = -1; //tail始终指向队尾。que[tail]是队尾。开始时队列为空,tail = -1
//队列长度等于tail-head+1
head++; //弹出队头元素,让head指向新队头。注意保持head <= tail
que[head]; //读队头
que[++tail] = data; //入队:先tail加1,然后数据data入队。注意tail必须小于N
这个手写代码有一个严重缺陷:如果进入队列的数据太多,使得tail超过了N,数组que[N]就会溢出,导致出错。
用下面的例子给出上述手写代码的应用。
约瑟夫问题 https://www.luogu.com.cn/problem/P1996
约瑟夫问题是一个经典问题,可以用队列、链表等数据结构实现。下面的代码用队列来模拟报数。如果不理解代码,可以模拟执行的过程。
#include <bits/stdc++.h>
using namespace std;
const int N = 10000; //定义队列大小,确保够用
int que[N];
int head=0, tail=-1;
int main(){
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++) que[++tail] = i;
while((tail-head+1)!=0){
for(int i=1;i<m;i++){
que[++tail] = que[head];
head++;
}
cout << que[head] << " ";
head++;
}
cout<<endl;
return 0;
}
代码第3行定义了队列的容量N = 10000。本题的n最大是100,每人出圈一次,所以队列长度一定不超过100×100。如果把N设置小了,例如N=2000,提交到OJ会返回RE,即Runtime Error,说明溢出了。
如果要防止溢出,可以使用循环队列。在上面例子中,只需要设置一个N=100的循环队列即可。
手写循环队列的代码见:《算法竞赛》第8页“1.2.2 手写循环队列”。
队列是一种线性数据结构,线性数据结构的主要缺点是查找较慢。要在队列中查找某个元素,只能从头到尾一个个查找。
2.1.2 Java手写队列
下面是Java的手写队列代码,和C++代码基本一样。
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int m = sc.nextInt();
int[] que = new int[10000]; // 定义队列大小,确保够用
int head = 0, tail = -1;
for (int i = 1; i <= n; i++) que[++tail] = i;
while ((tail - head + 1) != 0) {
for (int i = 1; i < m; i++) {
que[++tail] = que[head];
head++;
}
System.out.print(que[head] + " ");
head++;
}
System.out.println();
}
}
2.1.3 Python手写队列
下面是Python的手写队列代码。这个手写队列是用list实现的,进队尾用append()实现,队列自动扩展,不会有溢出问题。
n, m = map(int, input().split())
que = [i for i in range(1, n+1)]
head, tail = 0, n-1 #队头和队尾
while tail - head + 1 != 0:
for i in range(1, m):
que.append(que[head])
head += 1
tail += 1
print(que[head], end=' ')
head += 1
2.2 C++ STL队列queue
C++STL官方文档:英文主页 https://en.cppreference.com/,或中文主页https://zh.cppreference.com/
queue的文档:https://en.cppreference.com/w/cpp/container/queue
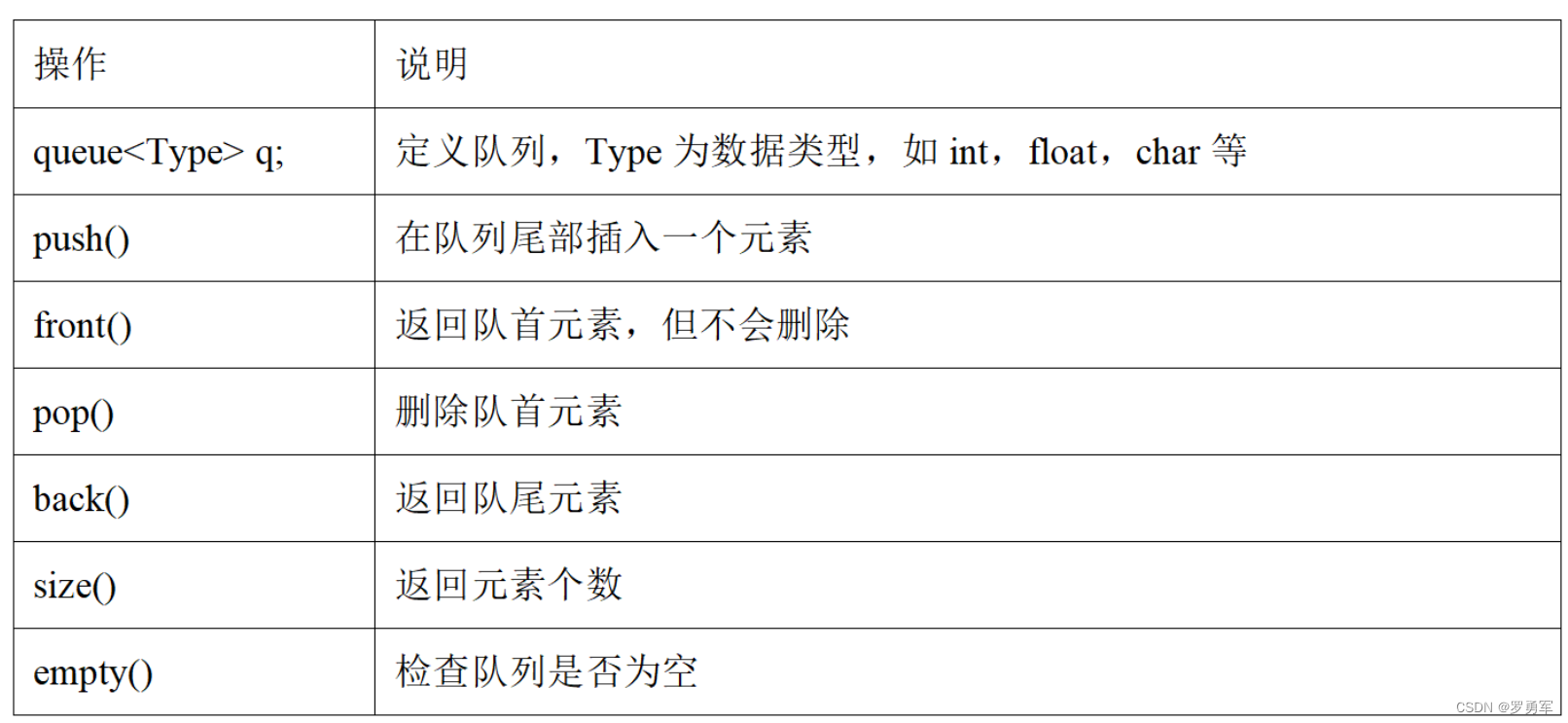
竞赛时一般不自己手写队列,而是用STL queue,而且没有溢出的问题,大大加快了做题速度。STL queue的主要操作见下表。
这里有篇博文可以参考:STL queue
下面是 约瑟夫问题 的STL queue实现。
#include <bits/stdc++.h>
using namespace std;
int main(){
int n,m;
cin>>n>>m;
queue<int>q;
for(int i=1;i<=n;i++) q.push(i);
while(!q.empty()){
for(int i=1;i<m;i++){
q.push(q.front());
q.pop();
}
cout << q.front() << " ";
q.pop();
}
cout<<endl;
return 0;
}
2.3 Java队列Queue
Java官方文档:https://docs.oracle.com/en/java/
Queue的文档:https://docs.oracle.com/en/java/javase/15/docs/api/java.base/java/util/Queue.html
Java用LinkedList实现基本队列Queue。常用操作有:

这篇博文可以参考:Java队列
下面是 约瑟夫问题 的Java Queue实现。
import java.util.LinkedList;
import java.util.Queue;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int m = sc.nextInt();
Queue<Integer> q = new LinkedList<>();
for (int i = 1; i <= n; i++) q.offer(i);
while (!q.isEmpty()) {
for (int i = 1; i < m; i++) {
q.offer(q.peek());
q.poll();
}
System.out.print(q.peek() + " ");
q.poll();
}
}
}
2.4 Python队列Queue和deque
Python官方文档:https://docs.python.org/3/
deque文档:https://docs.python.org/3/library/collections.html#collections.deque
Python的队列可以用list、Queue、deque实现。
下面先用Queue实现 约瑟夫问题 。
from queue import Queue
n, m = map(int, input().split())
q = Queue()
for i in range(1, n+1): q.put(i)
while not q.empty():
for i in range(1, m): q.put(q.get())
print(q.get(), end=' ')
不过,建议算法竞赛只使用deque,不要用queue。算法竞赛的代码都是单线程的,在这种场景下,deque比Queue快很多。
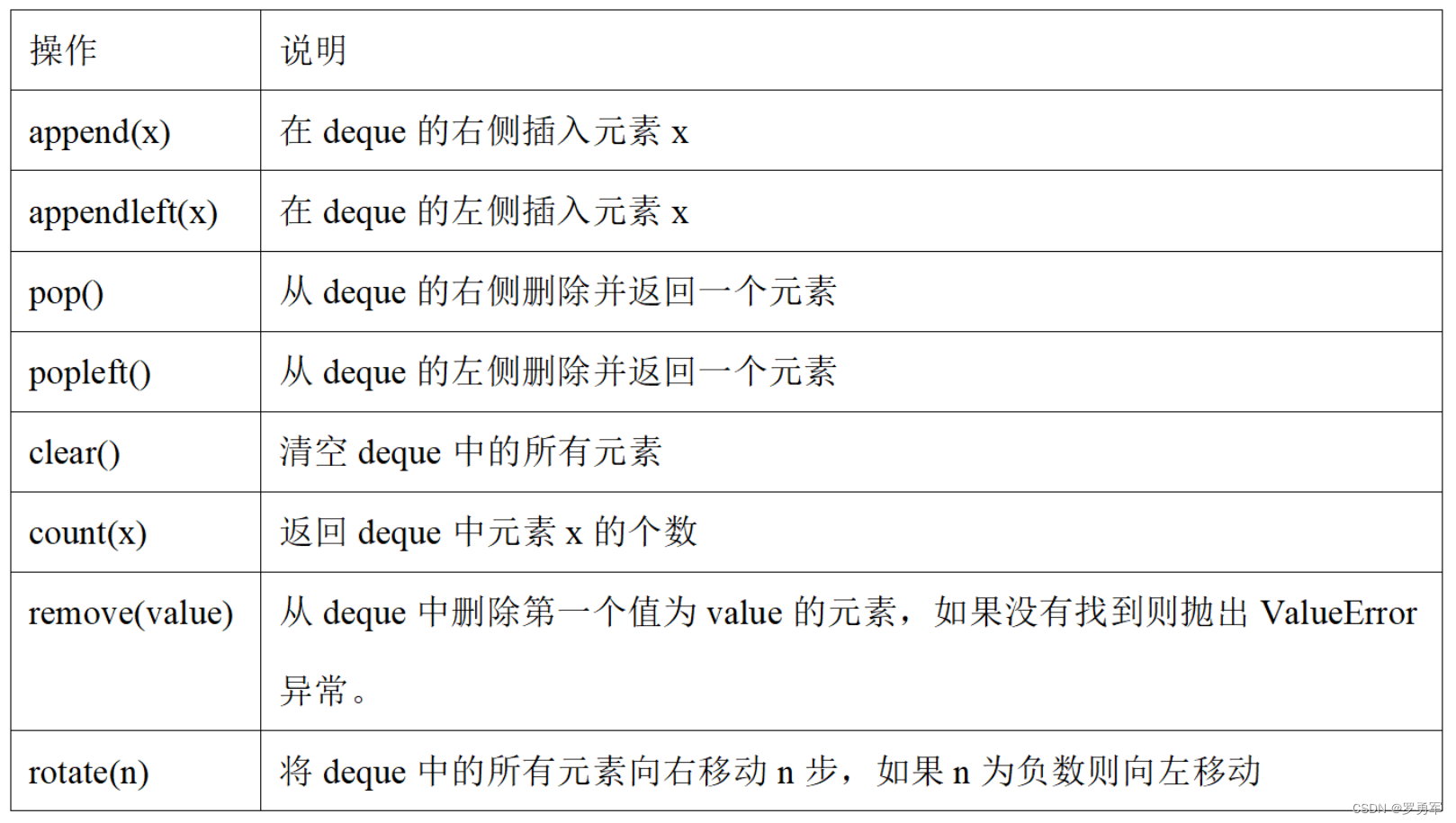
deque是双向队列,队头和队尾都能插入和弹出。当成普通队列使用时,只用它的队头弹出、队尾插入功能即可。deque的常用操作有:
参考博文:Deque
下面用deque实现 约瑟夫问题 。
from collections import deque
n, m = map(int, input().split())
dq = deque(range(1, n+1))
while dq:
dq.rotate(-(m-1)) #把前m-1个数挪到队列尾部
print(dq.popleft(), end=' ') #队头是第m个数,删除并打印它。
2.5 例题
机器翻译
用一个哈希表hashtable[]模拟内存,若hashtable[x]=true,表示x在内存中,否则不在内存中。用队列queue对输入的单词排队,当内存超过M时,删除队头的单词。
2.5.1 C/C++代码
#include <bits/stdc++.h>
using namespace std;
bool hashtable[1003]; //全局数组,自动初始化为0
int main(){
int m,n;
cin >> m >> n;
int ans=0; //函数内部变量,一定要初始化为0
queue<int> q;
for(int i=0;i<n;i++) {
int x; cin >> x;
if(hashtable[x] == false) {
hashtable[x] = true;
if(q.size() < m) q.push(x);
else {
hashtable[q.front()] = false;
q.pop();
q.push(x);
}
ans++; //内存中没有这个单词,到外存找,答案加1
}
}
cout << ans << '\n';
return 0;
}
2.5.2 Java代码
import java.util.*;
public class Main {
static boolean[] hashtable = new boolean[1003];
static Queue<Integer> q = new LinkedList<>(); //使用LinkedList实现队列
public static void main(String[] args) {
int m, n;
Scanner scanner = new Scanner(System.in);
m = scanner.nextInt();
n = scanner.nextInt();
int ans=0;
for (int i = 0; i < n; i++) {
int x = scanner.nextInt();
if (hashtable[x] == false) {
hashtable[x] = true;
if (q.size() < m)
q.add(x); //使用add方法添加元素到队列中
else {
//int front = ; //使用poll方法取出队列头部元素并移除
hashtable[q.poll()] = false;
q.add(x);
}
ans++;
}
}
System.out.println(ans);
}
}
2.5.3 Python
from collections import deque
hashtable = [False] * 1003 # 哈希表初始化,默认为False
m, n = map(int, input().split()) # 输入m和n
ans = 0 # 初始化答案为0
q = deque() # 初始化队列
line = list(map(int, input().split())) #读第2行
for x in line: #处理每个数
if hashtable[x] is False: # 如果x不在哈希表中
hashtable[x] = True # 将x加入哈希表
if len(q) < m: # 如果队列未满
q.append(x) # 将x加入队列
else: # 如果队列已满
hashtable[q.popleft()] = False # 将队列首元素出队并从哈希表中删除
q.append(x) # 将x加入队列
ans += 1 # 答案加1
print(ans) # 输出答案
3. 习题
https://www.lanqiao.cn/problems/3745/learning/
https://www.lanqiao.cn/problems/3746/learning/