论文:https://arxiv.org/pdf/2311.02877.pdf
简介
随着检测器的迅速发展, 边框回归取得了巨大的进步。然而,现有的基于 IoU 的边框回归仍聚焦在通过加入新的损失项来加速收敛,忽视 IoU 损失项其自身的限制。尽管理论上 IoU 损失能够有效描述边框回归状态,在实际应用中,它无法根据不同检测器与检测任务进行自我调整,不具有很强的泛化性。基于以上,我们首先分析了 BBR 模式,得出结论在回归过程区分不同回归样本并且使用不同尺度的辅助边框计算损失能够有效加速边框回归过程。对于高 IoU 样本,使用较小的辅助边框计算损失能够加速收敛,而较大辅助边框适用于低 IoU 样本。接着,我们提出了 Inner-IoU Loss, 其通过辅助边框计算 IoU 损失。针对不同的数据集与检测器,我们引入尺度因子 ratio 控制辅助边框的尺度大小用于计算损失。最后,将 Inner-IoU 集成至现有的基于 IoU 损失函数中进行仿真实验与对比实验。实验结果表明在使用本文所提出方法后检测效果得到进一步提升,验证了本文方法的有效性以及泛化能力。
本文贡献:
• 分析边框回归过程与模式,基于边框回归问题自身特性,提出在模型训练过程中使用较小的辅助边框计算损失对高IoU 样本的回归有增益效果,低IoU样本则与之相反。
• 提出了Inner-IoU Loss ,使用尺度因子ratio控制生成不同尺度的辅助边框用于计算损失。将其应用至现有IoU-based 损失函数中能够获得更快更为有效的回归结果。
• 进行了一系列仿真实验与对比实验,实验结果表明本文方法的检测效果与泛化性优于现有方法,并且适用于不同尺度的数据集达到了SOTA。
1.边框回归模式分析
IoU 损失函数在计算机视觉任务中具有广泛的应用。在边框回归过程中不但能够评估回归状态的好坏,而且能够通过计算回归损失进行梯度传播从而加速收敛。在这我们讨论回归过程中IoU 变化与边框尺寸的关系,分析边框回归问题的自身特性,解释本文所提出方法的合理性。

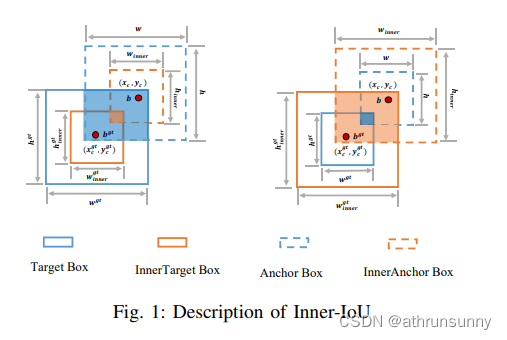
如上图所示,其中图a 为IoU-Deviation 曲线图,其水平轴与竖直轴分别表示deviation与IoU 值,三种不同颜色曲线对应不同尺度边框的IoU 变化曲线。A,B,C,D,E 分别对应achors and GT 框5 种不同位置关系,其中红色边框代表长宽为10 的anchors, 其对应的GT 框用黑色边框表示。图b 为ABS(Grad)-Deviation 曲线图,与图a 所不同的是在图b 中纵轴表示IoU 梯度的绝对值。我们假设实际边框尺寸为10,尺寸为8 和12 的边框作为其辅助边框。在图a与图b 中A,E 对应低IoU 样本回归状态,B,D 对应高IoU 样本回归状态,由图1可以得到以下结论。
1. 由于辅助边框与实际边框之间仅存在尺度差异,在回归过程中其IoU 值的变化趋势与实际边框的IoU值变化趋势一致,能够反应实际边框回归结果的质量。
2. 对于高IoU 样本,较小尺度的辅助边框的IoU梯度的绝对值大于实际边框IoU 梯度的绝对值。
3. 对于低IoU 样本,较大尺度的辅助边框的IoU梯度的绝对值大于实际边框IoU 梯度的绝对值。基于以上分析,使用较小尺度的辅助边框计算IoU 损失将有助于高IoU 样本回归,达到加速收敛的效果。与之相反使用较大尺度的辅助边框计算IoU 损失能够加速低IoU 样本回归过程。
2. Inner-IoU Loss
如图1所示,GT 框和锚框分别表示为和
。GT框和GT 框内部的中心点用
表示,而
则表示锚框和内部锚框的中心点。GT 框的宽度和高度分别表示为
和
,而锚框的宽度和高度分别表示为w 和h。变量”ratio ” 对应的是尺度因子,通常取范围为[0.5,1.5]。

Inner-IoU 的定义如下:

Inner-IoU损失继承了IoU损失的一些特性,同时具有自身的特性。和IoU损失一样Inner-IoU损失的取值范围为[0,1]。因为辅助边框与实际边框仅存在尺度上的差异,损失函数计算方式相同,InnerIoU-Deviation 曲线与IoU-Deviation曲线相似。与IoU损失相比,当ratio小于1,辅助边框尺寸小于实际边框,其回归的有效范围小于IoU损失,但其梯度绝对值大于IoU损失所得的梯度,能够加速高IoU样本的收敛。与之相反,当ratio大于1,较大尺度的辅助边框扩大了回归的有效范围,对于低Iou的回归有所增益。将Inner-IoU应用至现有基于IoU的边框回归损失函数中,定义如下:

在实验中作者证明了该方法的有效性,
在VOC数据集上ratio设置在[0.7,0.8]之间效果有明显提升

在AI-TOD数据集上ratio设置大于1效果有明显提升

yolo中改进
在utils/metrics.py文件中的bbox_iou替换为以下函数
import math
import torch
def bbox_iou(box1,
box2,
feat_sz,
xywh=True,
GIoU=False,
DIoU=False,
CIoU=False,
SIoU=False,
EIoU=False,
WIoU=False,
MPDIoU=False,
alpha=1,
scale=False,
monotonous=False,
ratio=1.0,
eps=1e-7):
"""
计算bboxes iou
Args:
feat_sz: 特征图大小
box1: predict bboxes
box2: target bboxes
xywh: 将bboxes转换为xyxy的形式
GIoU: 为True时计算GIoU LOSS (yolov5自带)
DIoU: 为True时计算DIoU LOSS (yolov5自带)
CIoU: 为True时计算CIoU LOSS (yolov5自带,默认使用)
SIoU: 为True时计算SIoU LOSS (新增)
EIoU: 为True时计算EIoU LOSS (新增)
WIoU: 为True时计算WIoU LOSS (新增)
MPDIoU: 为True时计算MPDIoU LOSS (新增)
alpha: AlphaIoU中的alpha参数,默认为1,为1时则为普通的IoU,如果想采用AlphaIoU,论文alpha默认值为3,此时设置CIoU=True则为AlphaCIoU
scale: scale为True时,WIoU会乘以一个系数
monotonous: 3个输入分别代表WIoU的3个版本,None: origin v1, True: monotonic FM v2, False: non-monotonic FM v3
ratio: Inner-IoU对应的是尺度因子,通常取范围为[0.5,1.5],原文中VOC数据集对应的Inner-CIoU和Inner-SIoU设置在[0.7,0.8]之间有较大提升,
数据集中大目标多则设置<1,小目标多设置>1
eps: 防止除0
Returns:
iou
"""
# Returns Intersection over Union (IoU) of box1(1,4) to box2(n,4)
# Get the coordinates of bounding boxes
if xywh: # transform from xywh to xyxy
(x1, y1, w1, h1), (x2, y2, w2, h2) = box1.chunk(4, -1), box2.chunk(4, -1)
w1_, h1_, w2_, h2_ = w1 / 2, h1 / 2, w2 / 2, h2 / 2
b1_x1, b1_x2, b1_y1, b1_y2 = x1 - w1_, x1 + w1_, y1 - h1_, y1 + h1_
b2_x1, b2_x2, b2_y1, b2_y2 = x2 - w2_, x2 + w2_, y2 - h2_, y2 + h2_
else: # x1, y1, x2, y2 = box1
b1_x1, b1_y1, b1_x2, b1_y2 = box1.chunk(4, -1)
b2_x1, b2_y1, b2_x2, b2_y2 = box2.chunk(4, -1)
w1, h1 = b1_x2 - b1_x1, (b1_y2 - b1_y1).clamp(eps)
w2, h2 = b2_x2 - b2_x1, (b2_y2 - b2_y1).clamp(eps)
# Intersection area
inter = (b1_x2.minimum(b2_x2) - b1_x1.maximum(b2_x1)).clamp(0) * \
(b1_y2.minimum(b2_y2) - b1_y1.maximum(b2_y1)).clamp(0)
# Union Area
union = w1 * h1 + w2 * h2 - inter + eps
if scale:
wise_scale = WIoU_Scale(1 - (inter / union), monotonous=monotonous)
# IoU
# iou = inter / union # ori iou
iou = torch.pow(inter / (union + eps), alpha) # alpha iou
feat_h, feat_w = feat_sz
# Inner-IoU
if xywh:
inner_b1_x1, inner_b1_x2, inner_b1_y1, inner_b1_y2 = x1 - w1_ * ratio, x1 + w1_ * ratio, \
y1 - h1_ * ratio, y1 + h1_ * ratio
inner_b2_x1, inner_b2_x2, inner_b2_y1, inner_b2_y2 = x2 - w2_ * ratio, x2 + w2_ * ratio, \
y2 - h2_ * ratio, y2 + h2_ * ratio
else:
x1, y1, x2, y2 = b1_x1, b1_y1, b2_x1, b2_y1
w1_, h1_, w2_, h2_ = w1 / 2, h1 / 2, w2 / 2, h2 / 2
inner_b1_x1, inner_b1_x2, inner_b1_y1, inner_b1_y2 = x1 - w1_ * ratio, x1 + w1_ * ratio, \
y1 - h1_ * ratio, y1 + h1_ * ratio
inner_b2_x1, inner_b2_x2, inner_b2_y1, inner_b2_y2 = x2 - w2_ * ratio, x2 + w2_ * ratio, \
y2 - h2_ * ratio, y2 + h2_ * ratio
inner_inter = (torch.min(inner_b1_x2, inner_b2_x2) - torch.max(inner_b1_x1, inner_b2_x1)).clamp(0) * \
(torch.min(inner_b1_y2, inner_b2_y2) - torch.max(inner_b1_y1, inner_b2_y1)).clamp(0)
inner_union = w1 * ratio * h1 * ratio + w2 * ratio * h2 * ratio - inner_inter + eps
inner_iou = inner_inter / inner_union
if CIoU or DIoU or GIoU or EIoU or SIoU or WIoU or MPDIoU:
cw = b1_x2.maximum(b2_x2) - b1_x1.minimum(b2_x1) # convex (smallest enclosing box) width
ch = b1_y2.maximum(b2_y2) - b1_y1.minimum(b2_y1) # convex height
c_area = cw * ch + eps # convex area
if CIoU or DIoU or EIoU or SIoU or WIoU: # Distance or Complete IoU https://arxiv.org/abs/1911.08287v1
c2 = (cw ** 2 + ch ** 2) ** alpha + eps # convex diagonal squared
rho2 = (((b2_x1 + b2_x2 - b1_x1 - b1_x2) ** 2 + (
b2_y1 + b2_y2 - b1_y1 - b1_y2) ** 2) / 4) ** alpha # center dist ** 2
if CIoU: # https://github.com/Zzh-tju/DIoU-SSD-pytorch/blob/master/utils/box/box_utils.py#L47
v = (4 / math.pi ** 2) * (torch.atan(w2 / h2) - torch.atan(w1 / h1)).pow(2)
with torch.no_grad():
alpha_ciou = v / (v - iou + (1 + eps))
return inner_iou - (rho2 / c2 + torch.pow(v * alpha_ciou + eps, alpha)) # CIoU
elif EIoU:
rho_w2 = ((b2_x2 - b2_x1) - (b1_x2 - b1_x1)) ** 2
rho_h2 = ((b2_y2 - b2_y1) - (b1_y2 - b1_y1)) ** 2
cw2 = torch.pow(cw ** 2 + eps, alpha)
ch2 = torch.pow(ch ** 2 + eps, alpha)
return inner_iou - (rho2 / c2 + rho_w2 / cw2 + rho_h2 / ch2) # EIou
elif SIoU:
# SIoU Loss https://arxiv.org/pdf/2205.12740.pdf
s_cw, s_ch = (b2_x1 + b2_x2 - b1_x1 - b1_x2) * 0.5 + eps, (b2_y1 + b2_y2 - b1_y1 - b1_y2) * 0.5 + eps
sigma = torch.pow(s_cw ** 2 + s_ch ** 2, 0.5)
sin_alpha_1, sin_alpha_2 = torch.abs(s_cw) / sigma, torch.abs(s_ch) / sigma
threshold = pow(2, 0.5) / 2
sin_alpha = torch.where(sin_alpha_1 > threshold, sin_alpha_2, sin_alpha_1)
angle_cost = torch.cos(torch.arcsin(sin_alpha) * 2 - math.pi / 2)
rho_x, rho_y = (s_cw / cw) ** 2, (s_ch / ch) ** 2
gamma = angle_cost - 2
distance_cost = 2 - torch.exp(gamma * rho_x) - torch.exp(gamma * rho_y)
omiga_w, omiga_h = torch.abs(w1 - w2) / torch.max(w1, w2), torch.abs(h1 - h2) / torch.max(h1, h2)
shape_cost = torch.pow(1 - torch.exp(-1 * omiga_w), 4) + torch.pow(1 - torch.exp(-1 * omiga_h), 4)
return inner_iou - torch.pow(0.5 * (distance_cost + shape_cost) + eps, alpha) # SIou
elif WIoU:
if scale:
return getattr(WIoU_Scale, '_scaled_loss')(wise_scale), (1 - iou) * torch.exp(
(rho2 / c2)), iou # WIoU v3 https://arxiv.org/abs/2301.10051
return iou, torch.exp((rho2 / c2)) # WIoU v1
return inner_iou - rho2 / c2 # DIoU
elif MPDIoU:
d1 = (b2_x1 - b1_x1) ** 2 + (b2_y1 - b1_y1) ** 2
d2 = (b2_x2 - b1_x2) ** 2 + (b2_y2 - b1_y2) ** 2
mpdiou_hw_pow = feat_h ** 2 + feat_w ** 2
return inner_iou - d1 / mpdiou_hw_pow - d2 / mpdiou_hw_pow - torch.pow((c_area - union) / c_area + eps,
alpha) # MPDIoU
# c_area = cw * ch + eps # convex area
return inner_iou - torch.pow((c_area - union) / c_area + eps, alpha) # GIoU https://arxiv.org/pdf/1902.09630.pdf
return iou # IoU
class WIoU_Scale:
"""
monotonous: {
None: origin v1
True: monotonic FM v2
False: non-monotonic FM v3
}
momentum: The momentum of running mean
"""
iou_mean = 1.
_momentum = 1 - pow(0.5, exp=1 / 7000)
_is_train = True
def __init__(self, iou, monotonous=False):
self.iou = iou
self.monotonous = monotonous
self._update(self)
@classmethod
def _update(cls, self):
if cls._is_train: cls.iou_mean = (1 - cls._momentum) * cls.iou_mean + \
cls._momentum * self.iou.detach().mean().item()
@classmethod
def _scaled_loss(cls, self, gamma=1.9, delta=3):
if isinstance(self.monotonous, bool):
if self.monotonous:
return (self.iou.detach() / self.iou_mean).sqrt()
else:
beta = self.iou.detach() / self.iou_mean
alpha = delta * torch.pow(gamma, beta - delta)
return beta / alpha
return 1同时在loss.py中做如下修改
# iou = bbox_iou(pbox, tbox[i], CIoU=True).squeeze() # iou(prediction, target)
# lbox += (1.0 - iou).mean() # iou loss
obj_sz = (tobj.size()[2],tobj.size()[3])
iou = bbox_iou(pbox, tbox[i], feat_sz=obj_sz, CIoU=True, ratio=0.8)
if isinstance(iou, tuple):
if len(iou) == 2:
lbox += (iou[1].detach().squeeze() * (1 - iou[0].squeeze())).mean()
iou = iou[0].squeeze()
else:
lbox += (iou[0] * iou[1]).mean()
iou = iou[2].squeeze()
else:
lbox += (1.0 - iou.squeeze()).mean() # iou loss
iou = iou.squeeze()