OCC教学：拓扑

拓扑：1.介绍

几何限制

OCCT 曲面支持矩形修剪。布尔运算后可能会出现非矩形域。
![[Pasted image 20231115140418.png]]

如何存储剪切操作的结果？

拓扑的目的

一般来说，拓扑是描述对象局限性的一种手段。
![[Pasted image 20231115140611.png]]

OCC拓扑被用于用于描述：

物体的边界；
对象之间的连接（通过公共边界）。
拓扑实体称为形状（shapes）。

拓扑的定义

拓扑形状是根据这两个概念定义的：

抽象拓扑（TopoDS）：通过描述有界和有界对象之间的关系来定义数据结构。示例：边由其边界（即顶点）描述。
边界表示（B-Rep）：通过关联拓扑和几何信息来完成对象的定义。例子：一条边位于曲线上并以点为界。
边界表示和算法类被分组在不同的包中。

为什么使用边界表示（B-rep）

B-Rep 有多种替代方案：

构造立体几何（CSG）， CSG 不允许对任意数字进行建模。
表面模型，表面模型不适合下游工程作业。
线框模型，多个实体可以对应于相同线框模型（结果不唯一）。
网格模型，网格不支持弯曲几何体。
B-Rep 有一些缺点。它是脆弱的、冗长的、复杂的。 B-Rep模型使用顶点、边和面作为几何载体，但也具有特殊的拓扑类型。模型的复杂性导致脆弱性。

拓扑：2.抽象拓扑

拓扑形状（shapes）

OCCT定义了以下类型的拓扑形状：

Vertex 顶点：一个点；
Edge 边：由顶点限制的曲线的一部分；
Wire 线框：一组边（通过它们的顶点连接）；
Face 面：由线限制的表面的一部分；
Shell 壳：一组面（通过边连接）；
Solid 实体：受壳限制的空间的一部分；
Compsolid 复合实体：一组通过面连接的实体；
Compound 复合：任意拓扑形状的群。

拓扑结构图

下图显示了复杂形状（图中的实体）的子形状之间关系的示例：
![[Pasted image 20231115142801.png]]

形状（shapes）的连接性

如果两个形状（shapes）共享一些边界子形状，则它们是连接的。
示例：让我们考虑两条边——e1 和 e2。它们中的每一个都受到其边界的限制，边界是顶点（v1f 和 v1l是e1的边界）（v2f 和 v2l是e2的边界）。当这两条边共享一个公共顶点 v3 时，它们是连接的。
![[Pasted image 20231115143423.png]]

形状（shape）的层次结构

TopoDS_Shape 是所有拓扑形状类的基类。
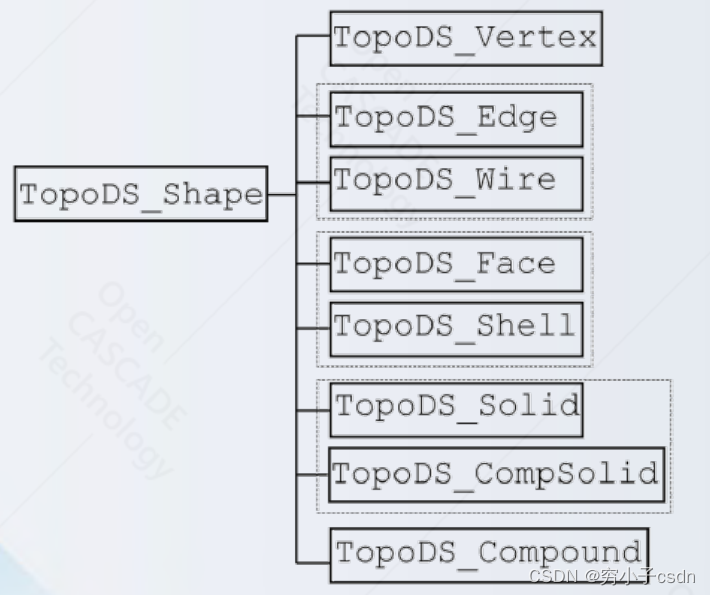
在这里插入图片描述

TopoDS_Vertex 保存有关点（零维对象）的信息；
TopoDS_Edge 保存有关曲线（一维对象）的信息；
TopoDS_Wire 是边的集合；
TopoDS_Face 保存有关表面（二维对象）的信息；
TopoDS_Shell 是面的集合；
TopoDS_Solid、TopoDS_Compsolid 保存有关实体的信息；
TopoDS_Compound 表示一个形状，它是形状的集合。

形状（shape）结构

TopoDS_Shape 类通过以下方式定义形状：

TopoDS_TShape 句柄（handle）（TopoDS package）；
局部坐标系（TopLoc package）;
方向（TopAbs package）。

TopoDS_TShape：一个句柄类，描述其对象在它默认坐标系。这个类从来没有直接使用过，通常使用 TopoDS_Shape。
TopLoc_Location：定义局部坐标系，将形状放置在与其定义不同的位置。
示例：所有这些盒子共享相同的 TShape，但位置不同。
![[Pasted image 20231115144358.png]]

TopAbs_Orientation：描述形状如何根据区域（内部和外部）界定几何形状。
![[Pasted image 20231115145008.png]]

考虑形状（shape）的上下文关系时，形状的方向和位置参数也被假定影响其子形状。当将一个形状发展为子形状时，子形状的方向和位置将与主形状的方向和位置相结合。这确保了在引用子形状的每个形状的上下文中对子形状的参数进行一致的解释。例如，当在这些面的上下文中搜索时，两个相连的面共享的边将具有相反的方向。

形状（shape）操作

TopoDS_Shape 类及其子类提供了各种有用的方法，例如：
访问 TShape：

IsNull() 检查 TShape 是否为 null；
Nullify() - 使 TShape 智能指针无效。
访问location：
Location() - 返回现有位置；
Move () - 对实际形状应用变换；
Moved() - 返回应用变换的新形状。
ShapeType() - 返回 TopoDS_Shape 的类型。
形状比较：
IsPartner()——相同的 TShape；
IsSame()——相同的 TShape 和位置；
IsEqual()——相同的 TShape、位置和方向。

向下转型（基类->子类）

TopoDS_Shape 对象通过值进行操作。这就是为什么要实现特殊方法来提供向下转换功能的原因：

TopoDS::Vertex() 返回一个 TopoDS_Vertex
TopoDS::Edge() 返回一个 TopoDS_Edge
TopoDS::Wire() 返回一个 TopoDS_Wire
TopoDS::Face() 返回一个 TopoDS_Face
TopoDS::Shell() 返回一个 TopoDS_Shell
TopoDS::Solid() 返回 TopoDS_Solid
TopoDS::CompSolid() 返回TopoDS_CompSolid
TopoDS::Compound() 返回一个 TopoDS_Compound
注意：当进行不适当的转换时会引发异常。
示例：第一个代码块是正确的，但第二个代码块被编译器报错。

形状（shape）的集合

TopTools 包提供：

用于计算具有或不具有方向的形状的哈希码的类。
形状集合的实例化。

搜索工具

搜索拓扑形状意味着找到它的子形状，可能符合特定的标准。

TopoDS_Iterator 类搜索给定形状的第一级子形状（来自其 TShape 中的列表）。
TopExp_Explorer 类搜索给定形状中的所有子形状，并可以选择实体类型（例如，仅面）。
TopExp::MapShapes() 方法搜索子形状并将它们放入map中（从而检测相同的元素）。
TopExp::MapShapesAndAncestors() 方法返回引用另一个实体的所有实体。

在OCCT中，不存在从子形状到其祖先形状的反向指针。相反，TopExp::MapShapesAndAncestors() 可用于恢复此信息。例如，如果您想查找包含给定顶点或边的所有面，您可以使用此方法。

拓扑：3.边界表示（B-rep)

边界表示

边界表示（B-Rep）在三维描述模型对象。
在 B-Rep 建模中，实体由其边界表示。
![[Pasted image 20231115151959.png]]

B-Rep 将几何融入拓扑：

几何形状：面位于曲面上，边位于曲线上，顶点位于点上。
拓扑：形状的连通性。
因此模型对象的描述就完成了。
B-Rep 描述基于：
TopoDS package——描述对象的拓扑结构。
Geom 和 Geom2d package——描述这些物体的几何形状。

B-Rep 实体

定义 BRep_TVertex、BRep_TEdge 和 BRep_TFace 是为了向拓扑模型添加几何信息。
BRep_TVertex、BRep_TEdge 和 BRep_TFace 继承 TopoDS_TShape。
根据拓扑实体的不同，几何信息的存储方式也不同。
存储几何信息的实体允许描述：

边：受顶点限制的曲线；
面：由边限制的曲面；
实体：受面限制的空间。

BRep_TVertex 中的几何图形

BRep_TVertex 几何存储为：3D 点 (gp_Pnt) ——对于所有顶点。
点表示的列表可以是：

曲线上的点（Geom_Curve，参数）——如果顶点界定边。
曲面上曲线上的点（Geom_Surface、Geom2d_Curve、参数）——如果顶点界定曲面上的边。
曲面上的一点(Geom_Surface, Uparameter, Vparameter)——如果顶点界定面。

BRep_TEdge 中的几何图形

BRep_TEdge 几何图形存储为曲线列表，可以是：

一条 3D 曲线和曲线上的两个参数（Geom_Curve、FirstParameter、LastParameter）。
曲面上的一条曲线，曲线上的两个参数和曲面上的两对参数（Geom2d_Curve、FirstParameter、LastParameter、Geom_Surface、FirstUVCoord、LastUVCoord）。
SameParameter 属性指示是否对边缘的不同表示进行参数化同步，即 3D 曲线上具有相同参数值的点与每条 2D 曲线重合（在边的公差范围内）

BRep_TFace 中的几何图形

BRep_TFace 几何图形存储为 Geom_Surface
![[Pasted image 20231115153915.png]]

B-Rep 的精度

一些几何表示可以附加到拓扑（B-Rep）对象。例如，一个顶点可以表示为：

3D点；
曲线上的参数；
曲面上的一对参数。
这些表示相似但很少相同。对于建模算法，有必要准确地知道与该近似值相关
的精度。该精度的数值与每个 B-Rep 形状相关联，称为公差。它定义了对象的
所有几何表示所在的区域。
在 BRep_TVertex 中，精度定义了围绕3D 点的球体的半径：

在 BRep_TEdge 中，精度定义了 3D 曲线周围管道的半径： ![[Pasted image 20231115162914.png]]

在 BRep_TFace 中，精度定义了曲面面上方和下方的厚度： ![[Pasted image 20231115163008.png]]

由于公差与几何载体相关，因此它是由 B-Rep 中创建或修改几何的算法定义的。
OCCT要求：公差(顶点) >= 公差(边) >= 公差(面)
![[Pasted image 20231115163106.png]]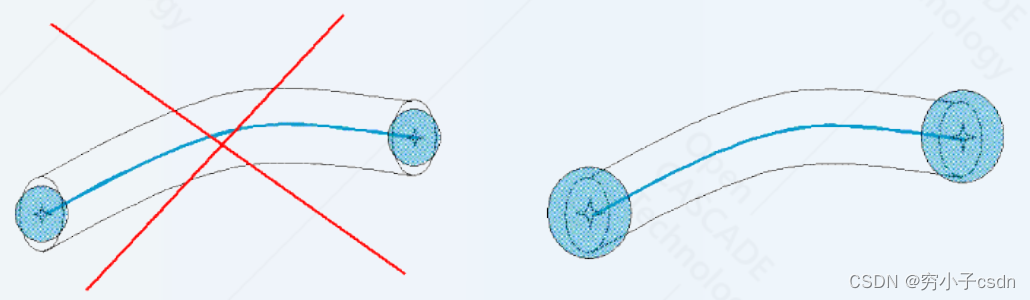 在这里插入图片描述

Package: BRepAdaptor

OCCT 使适配器用于通过适配器模式在几何算法中使用拓扑实体。边界表示作为修剪的曲线和曲面工作，从而消除了手动修剪的必要性。可以使用以下适配器：

BRepAdapter_Curve——接受边曲线适配器；
BRepAdapter_Curve2d——接受边和面的曲线适配器；
BRepAdapter_CompCurve——接受线框的曲线适配器；
BRepAdaptor_Surface——接受面的曲面适配器。
注意：可提供手柄版本的适配器。例如，BRepAdaptor_HSurface类是曲面适配器的手柄版本。

B-Rep 特点

3D 空间（3D 拓扑）和参数空间（UV 拓扑）中同一面的表示通常拓扑相似。
![[Pasted image 20231115164601.png]]
有时 3D 拓扑和 UV 拓扑是不同的。这是情况出现在接缝边和退化的边。

接缝边是定义封闭面上（通常构建在周期性曲面上）上的接缝的边。在这种情况下，一个 3D 拓扑对应于多个UV 拓扑。
当一条或多条 UV 2d 曲线对应于单个 3D 顶点时，称边已退化。此类边没有 3d 曲线表示，并且两次包含相同的顶点（方向相反）。

形状（shapes）构造

OCCT提供了多个软件包，为建模算法提供高级 API。这些 API 既简单又强大：

简单，因为只需要调用一次函数即可创建对象
功能强大，因为它包括错误处理和对算法提供的额外信息的访问

Package: BRepBuilderAPI

该包包含以下类：

从几何实体直接构造拓扑对象或从形状集合组合拓扑
- BRepBuilderAPI_MakeVertex：从点构建顶点；
- BRepBuilderAPI_MakeEdge、MakeEdge2d：从曲线构建边；
- BRepBuilderAPI_MakePolygon：从点构建线框；
- BRepBuilderAPI_MakeWire：从边构建线框；
- BRepBuilderAPI_MakeFace：从曲面构建面；
- BRepBuilderAPI_MakeShell：从曲面面构建外壳（分割为 C2 Patches）；
- BRepBuilderAPI_MakeSolid：从壳构建实体。
修改对象：
- RepBuilderAPI_Transform：对形状应用变换；
- BRepBuilderAPI_Copy：进行形状的深层复制；
- BRepBuilderAPI_Sewing：通过合并边界边从一组面构建外壳。
创建基本对象：
- BRepPrimAPI_MakeBox
- BRepPrimAPI_MakeWedge
- BRepPrimAPI_MakeSphere
- BRepPrimAPI_MakeCone
- BRepPrimAPI_MakeCylinder
- BRepPrimAPI_MakeTorus
- BRepPrimAPI_MakeHalfSpace
创建扫掠对象：
- BRepPrimAPI_MakePrism
- BrepPrimAPI_MakeRevol

位置修改

OCCT 中提供的数据共享概念允许重复使用拓扑信息和实例模型通过不同的位置。形状内的位置是一组连续的变换，它们是作为单个转换进行操作。
注意：空位置和现有的相同位置被视为不同。IsSame() 检查将返回 false。
位置方法如下：

Location
Move
Moved

方向：边内的顶点

OCCT方向概念旨在通过内部和外部区域的信息完成边界表示。该信息是一组影响形状正确性的规则。
方向本身对于顶点没有任何意义。仅当顶点限制某些边时，顶点方向才有
意义。边是使用一对顶点构造的（在周期曲线的情况下至少一个顶点使用两
次）；按照约定，第一个顶点具有 TopAbs_FORWARD 方向，第二个顶点具有 TopAbs_REVERSED 方向。
注意：BRepBuilderAPI_MakeVertex 构造一个具有 TopAbs_FORWARD 方向的顶点。
![[Pasted image 20231115171023.png]]

方向：线框内的边

面是由边界定的一部分曲面。边被组织成线框，以便能够单独跟踪每个环（外部或内部）。
当相框是自由时，没有任何限制；可以无限制地将边添加到线框上。
当线框属于面时，右手法则起作用；线框中的每个边应根据曲线上参数增加的方向定向，使内部位于左侧。
![[Pasted image 20231115171720.png]]

可以重建曲线，但更好的做法是复原基础曲线。第二选项是在OCCT中重建。

方向：实体中的面

实体是模型空间的一部分，由组织成壳的面界定。实体中的法线应该指向实体外部。微分几何指出可以通过曲面上的点计算曲面法向，使用以下公式（“x”代表叉积）： $N(u_{0},v_{0})=s_{u}'(u_{0},v_{0})\times s_{v}'(u_{0},v_{0})$
法向计算得到方向的符号，因此存在交换偏导数的替代公式（OCCT 使用上面提供的公式）。如何保证实体中正确的法线方向？
面方向在法线之前决定符号：

TopAbs_FORWARD——方向根据上述公式进行计算
TopAbs_REVERSED——法向被乘以-1.0
注意：实体可以表示除由实体边界界定的部分空间之外的整个模型空间。法线
在这种情况下将指向空间的有界部分内部。

拓扑：4.建模应用接口（API）

建模API：BRepAlgoAPI

OCCT 有两种布尔算法的实现。在内部，它们被称为“旧”和“新”算法。旧算法不再维护并标记为已过时。 OCCT 的“新”布尔算法可在 BRepAlgoAPI package中找到。可以使用以下算法：

相减 Cut（BRepAlgoAPI_Cut）;
并集 Fuse（BRepAlgoAPI_Fuse）。
相交 Common（BRepAlgoAPI_Common）。
相交线 Section（BRepAlgoAPI_Section）。
分离器 Splitter（BRepAlgoAPI_Splitter）。

建模API：BRepOffsetAPI

该软件包提供了额外的构建工具，例如：

BRepOffsetAPI_ThruSections——从一组轮廓放样（loft）构建壳体或实体；
BRepOffsetAPI_DraftAngle——使用给定的角度信息锥化一个形状的面集；
BRepOffsetAPI_MakeOffsetShape——在给定形状上构建偏移形状；
BRepOffsetAPI_MakeThickSolid——根据给定实体和要删除的面集构建空心实体；
BRepOffsetAPI_MakePipe——通过沿着导线（spine）扫掠形状轮廓（profile）来构建管道形状（用于创建管道（Pipe）形状，通常是通过沿着一条给定的曲线生成具有不同截面的形状。这是一种通过定义路径和截面来创建具有变化横截面的几何体的方法）；
BRepOffsetAPI_MakeEvolved——从平面或线（spine）和轮廓（profile）构建可展形状（是一个更一般化的工具，用于创建演化（Evolved）形状。它可以处理更复杂的几何演变，包括旋转、放样、扭曲等。与 BRepOffsetAPI_MakePipe不同，BRepOffsetAPI_MakeEvolved可以执行更广泛的形状演变操作）