文献思想

作者发现不同循环寿命的电池，第100次和第10次循环放电容量的差有不同，作者由这一现象，提取出了放电容量差的方差、平均值、最小值等特征，其中放电容量差的方差对数和循环寿命的对数的皮尔逊相关性高达-0.93，然后由此系列特征，用回归模型对循环寿命做估计，最好的模型使用前100个循环的数据预测周期寿命时，有9.1%的测试误差，此时大多数电池还没有表现出容量退化。除此之外，本文还对电池做了低寿命组和高寿命组的分类，仅使用前5个循环数据对电池分类，有4.9%的测试误差。另作者认为石墨负极在这些电池的降解中占主导地位，这些结果可能对其他基于石墨的锂离子电池也很有用。

复现过程

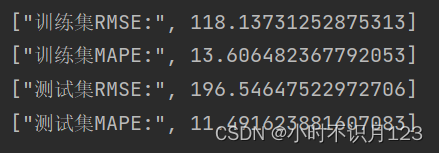
评测指标：MAPE和RMSE
总数据集：124
测试集：40

Fig. 1

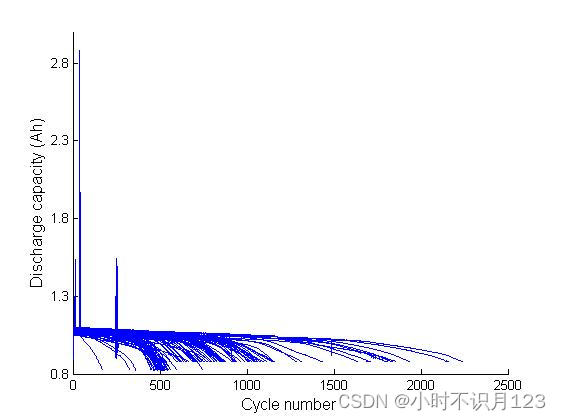
a : 124块电池每次循环时总放电容量与循环数的关系,容量衰减轨迹的交叉说明了初始容量与寿命之间的弱关系;和文献里的图略有不同：文献中的图只保留了电池的前1000次循环，这里画出了电池的整个生命周期。

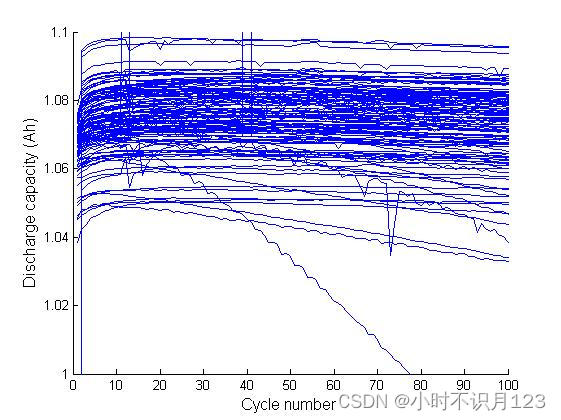
b : a的详细视图，只显示前100个循环，到100个循环时，还没有出现明显的寿命衰减。

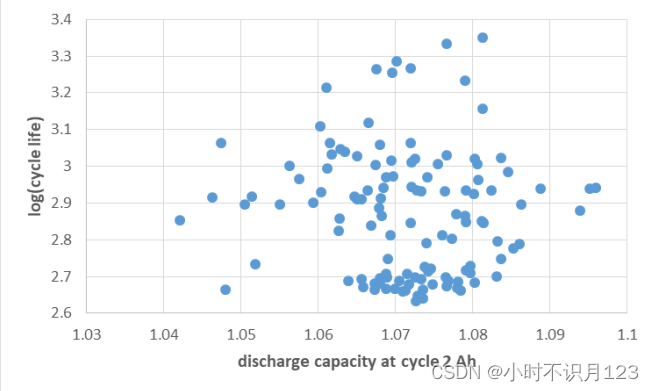
d : 循环2时的总放电容量与循环寿命对数的相关系数为-0.061。

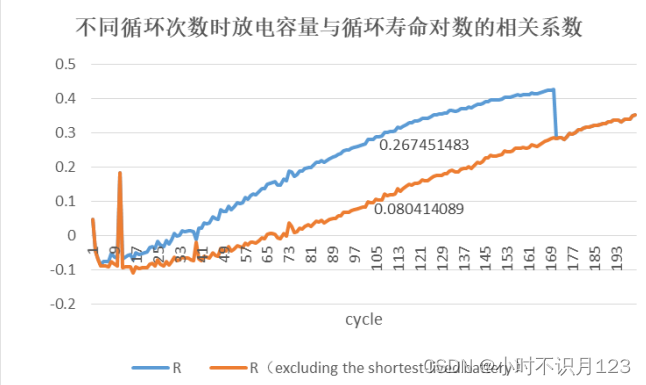
e : 循环100时的总放电容量与循环寿命对数的相关系数为0.27（排除寿命最短的电池后为0.08）。这里是文献图的延申：这里画的是循环从1到200时，分别对应的相关系数.

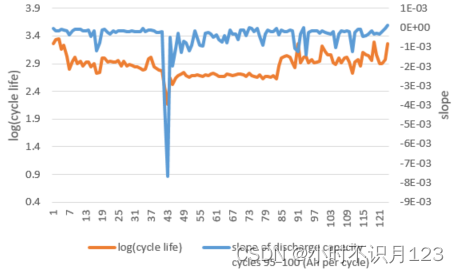
f : 循环寿命95和100的总放电容量差值和循环寿命对数的相关系数是0.479。

Fig. 2

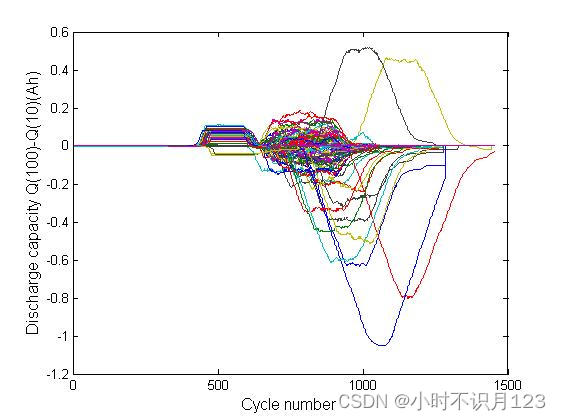
b : 124个电池的第100次和第10次循环的放电容量曲线的差值图示，ΔQ100-10(V)。
下图便是论文作者的核心思想：不同循环寿命的电池，容量差不一样。
原始图：

放电容量差值后的图

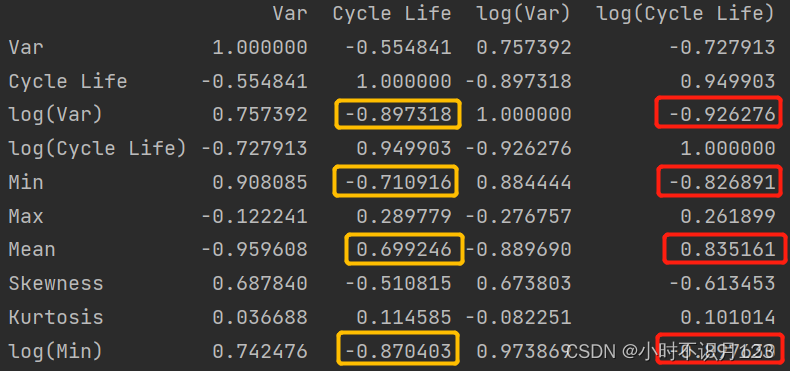
c ： 循环寿命的对数和ΔQ100-10(V)的方差的相关系数为-0.93。

Table 1

‘Variance’ model
和原文一致，测试集上rmse为196，mape为11.4%。

思考

本文中同一块电池的工况一直都是保持一致的，实车工况复杂。
实车效果验证周期性太长了。

代码

数据表头：

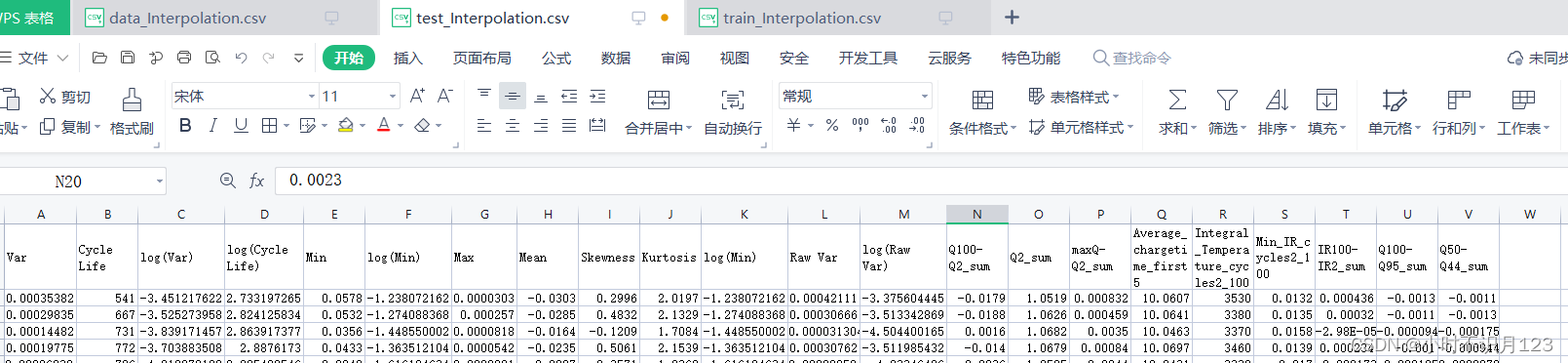
import pandas as pd, numpy as np
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import r2_score, mean_squared_error, mean_absolute_error, mean_absolute_percentage_error
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
import json
from sklearn.ensemble import BaggingRegressor
from sklearn import tree
from sklearn import linear_model
from sklearn import svm
from sklearn import neighbors
from sklearn import ensemble
from sklearn import ensemble
from sklearn import ensemble

plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']
plt.rcParams['axes.unicode_minus'] = False

data = pd.read_csv('data/train_Interpolation.csv', header = 0)
x_columns = [x for x in data.columns if x in ['log(Var)']]
# x_columns = [x for x in data.columns if x in ['log(Min)','log(Var)','Skewness','Kurtosis','Q2_sum','maxQ-Q2_sum']]
# x_columns = [x for x in data.columns if x in ['log(Min)','log(Var)','Q2_sum','Average_chargetime_first5',"Integral_Temperature_cycles2_100",'Min_IR_cycles2_100','IR100-IR2_sum','Q50-Q44_sum']]
# x_columns = [x for x in data.columns if x in ['log(Min)','log(Var)','Skewness','Kurtosis','Q2_sum','maxQ-Q2_sum','Average_chargetime_first5',"Integral_Temperature_cycles2_100",'Min_IR_cycles2_100','IR100-IR2_sum','Q50-Q44_sum']]
x_train = data[x_columns].dropna()
y_train = data['log(Cycle Life)'].dropna()

data = pd.read_csv('data/test_Interpolation.csv', header = 0)
x_columns = [x for x in data.columns if x in ['log(Var)']]
x_test = data[x_columns].dropna()
y_test = data['log(Cycle Life)'].dropna()

# 随机划分成训练集和测试集, test_size表示比例（这里训练集：测试集=8:2)
# x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3,shuffle=True)

rf1 = tree.DecisionTreeRegressor()
rf2 = linear_model.LinearRegression()
# rf2=linear_model.Lasso(alpha = 0.0009,fit_intercept=False,warm_start=True)
rf3 = svm.SVR()
rf4 = neighbors.KNeighborsRegressor()
rf5 = ensemble.RandomForestRegressor(n_estimators = 20, max_depth = 5)
rf6 = ensemble.AdaBoostRegressor(n_estimators = 50)
rf7 = ensemble.GradientBoostingRegressor(n_estimators = 100)
rf8 = BaggingRegressor()

rf = rf2.fit(x_train, y_train)

y_train_pred = 10 ** (rf.predict(x_train))
y_test_pred = 10 ** (rf.predict(x_test))
y_train = 10 ** y_train
y_test = 10 ** y_test

print(json.dumps(('训练集RMSE:', mean_squared_error(y_train, y_train_pred) ** 0.5),
                 ensure_ascii = False))
print(json.dumps(('训练集MAPE:', mean_absolute_percentage_error(y_train, y_train_pred) * 100),
                 ensure_ascii = False))

print(json.dumps(('测试集RMSE:', mean_squared_error(y_test, y_test_pred) ** 0.5),
                 ensure_ascii = False))
print(json.dumps(('测试集MAPE:', mean_absolute_percentage_error(y_test, y_test_pred) * 100),
                 ensure_ascii = False))


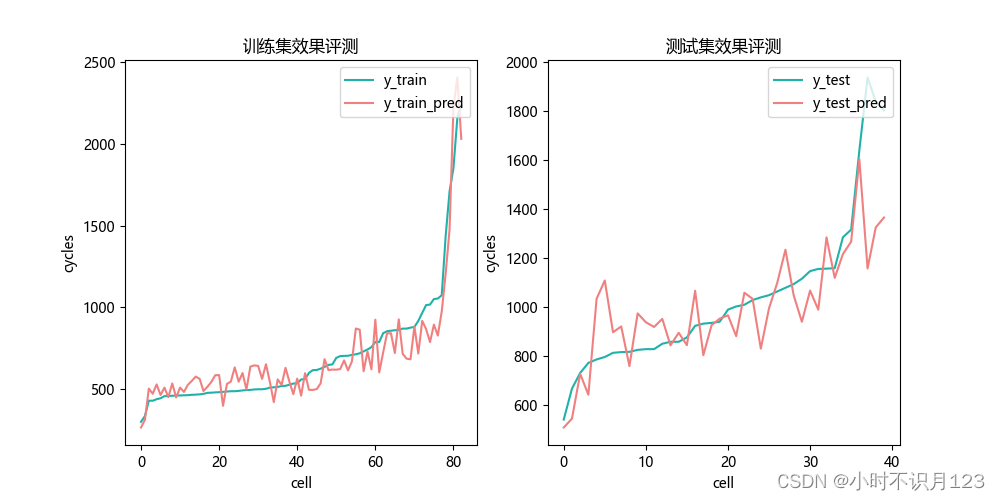
def plotF(y_train, y_train_pred, y_test, y_test_pred):
    plt.figure(figsize = (10, 5))
    plt.subplot(121)
    plt.plot(np.arange(len(y_train)), y_train, '#20B2AA', label = 'y_train')
    plt.plot(np.arange(len(y_train_pred)), y_train_pred, '#F08080', label = 'y_train_pred')
    plt.legend(loc = 1)
    plt.xlabel('cell')
    plt.ylabel('cycles')
    plt.title('训练集效果评测')

    plt.subplot(122)
    plt.plot(np.arange(len(y_test)), y_test, '#20B2AA', label = 'y_test')
    plt.plot(np.arange(len(y_test)), y_test_pred, '#F08080', label = 'y_test_pred')
    plt.legend(loc = 1)
    plt.xlabel('cell')
    plt.ylabel('cycles')
    plt.title('测试集效果评测')
    plt.show()


def corrF():
    pd.set_option('display.max_columns', None)
    pd.set_option('display.max_rows', None)
    data = pd.read_csv('data/data_Interpolation.csv', header = 0)
    print(data.corr())

附录

数据进一步说明

124块商用LFP/石墨电池，A123 Systems，型号APR18650M1A，标称容量1.1Ah，额定电压为3.3V，制造商推荐的快充协议是3.6C恒定电流-恒定电压 (CC-CV)。

恒温环境室(30°C)中，不同的快速充电条件，相同的放电条件下进行循环，循环寿命从150次到2300次不等。
充电时：采用 "C1(Q1)-C2"的策略，C1和C2分别是第一和第二恒定电流步骤，Q1是电流切换时的充电状态（SOC，%），第二个电流步骤在80%的SOC时结束，此后电池以1C CC-CV充电到3.6V 及C/50的电流截止点。
放电时：4C到2.0V，其中1C为1.1A，先恒流再恒压。
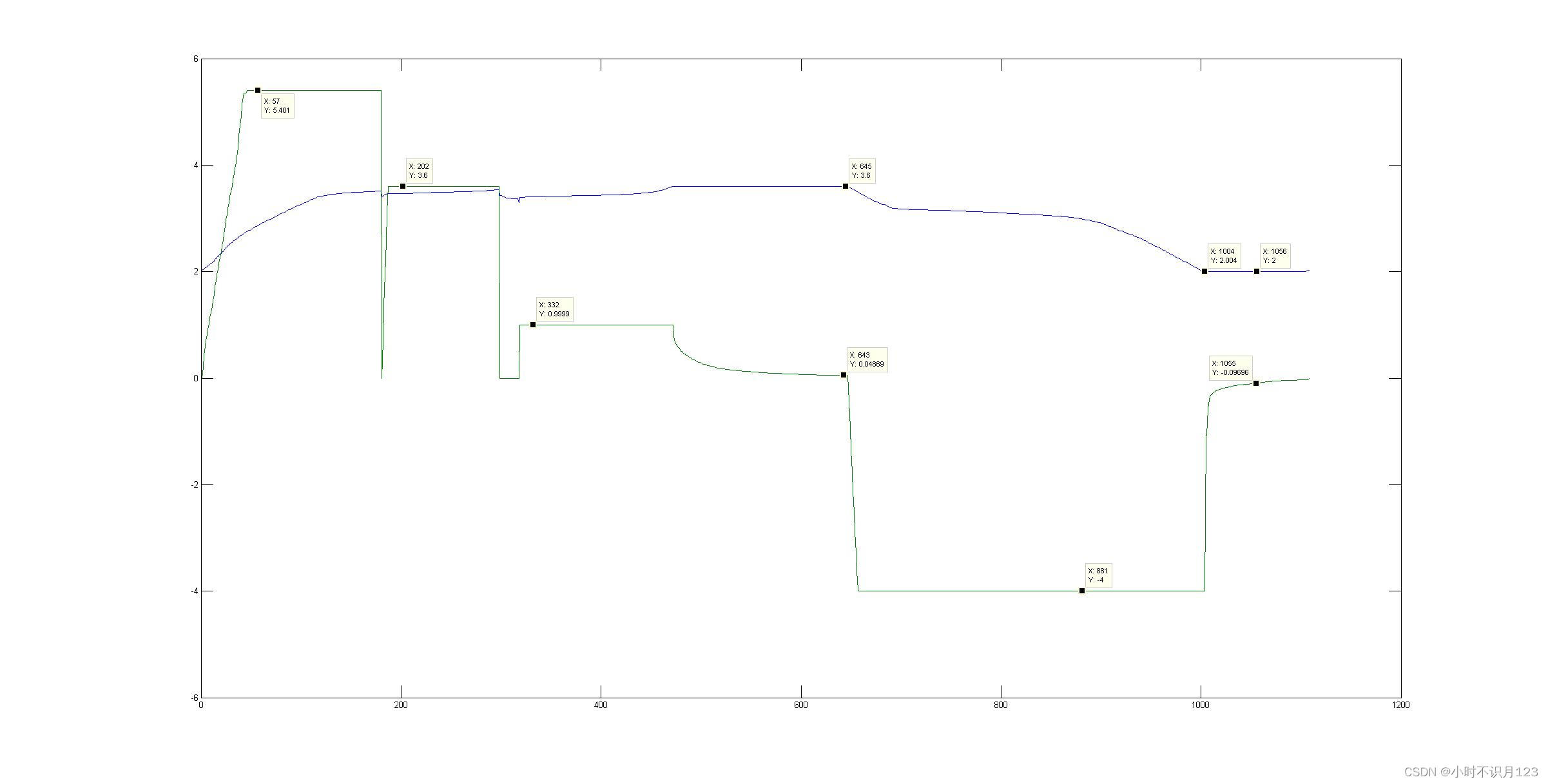
'5.4C(40%)-3.6C’的充电策略如下：