在运筹学领域的经典模型中，最大流问题、多商品网络流问题和最短路径问题等都依附在图上对问题进行描述，同样，当我们梳理问题的数学模型，或理解相关问题的求解算法时，也要依靠它。因此，我将总结和图相关的问题，并梳理各类问题的求解算法。本文先对寻找有向无权图最短路径的方法进行小结。

图的定义和种类

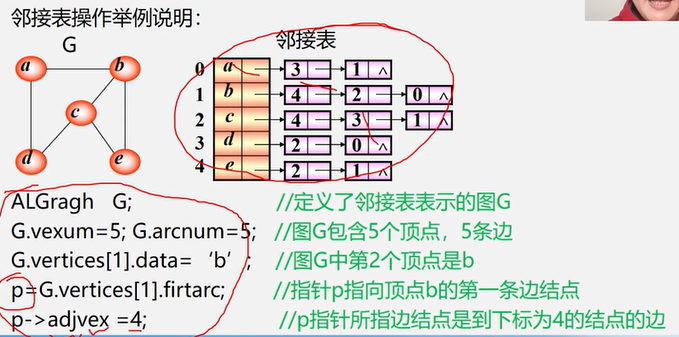
如上所示，在一个图中有两个重要的组成元素，分别是节点和边，通常我们会把节点集合记作 V = { v 1 , v 2 . . . v n } V=\lbrace v_1,v_2...v_n \rbrace V={v1​,v2​...vn​}，将边记作 E = { e 1 , e 2 , . . . e m } E=\lbrace e_1,e_2,...e_m \rbrace E={e1​,e2​,...em​}，这样就可以用数学方式表示出来一个图$G=(V,E)$。图中的节点可以表示实际生活中的对象，节点之间的边可以理解为对象之间的特定关系；比如，可以将上图中每个节点想象为每个城市的火车站，那边就可以看作两座城市的火车站之间可以通车。

有了图的基本概念后，伴随着各种各样的问题，就有了形形色色的图。假设还把它理解为城市之间的火车站连通情况，现在我想在这副图上表示出两个城市之间火车通车的时间，那我就可以给每条边加上权重，这样它就变成了无向有权图；如果车站之间是单程的（只是假定），那我就可以给每条边加上方向，这样就得到一个有向有权图 。下图是一个有向有权图。

寻找有向无权图最短路径

在有向无权图中，我们将相邻节点之间的路径长度定义为$1$。寻找有向无权图的最短路径，即给定一个起点和终点后，找到一个从起点到终点距离最短的路径； 也可以理解为从起点经过最少数量的节点，到达终点（仅限有向无权图）。

求解有向无权图的最短路径算法中， 给算法输入一个图和起点，就可以得到从起点到各点的最短路径。接下来以上图为例，讲述算法的求解过程。

初始化阶段，准备一个Queue，并初始化一个Status table，如下表所示。

在Status table中，有四列，第一列是图中的节点名称，第二列表示该节点有没有被访问过，初始时所有节点设置为$no$，第三列$dist$表示该节点与起点之间的距离，初始时设置为$inf$，即为无限远；第四列为该节点在最优路径中对应的前置节点，初始时设置为$0$。

• 初始化

我们假设起点为$v_3$，寻找到剩余节点的最短路径。在初始化阶段，将Status table中的起点$v_3$的$visit$设置为$yes$，自己和自己的距离为$0$，设置$dist$为0。同时，将起点$v_3$放入Queue中。这些完成后，我们可以进行第一轮循环。

• Iteration 1
  • 从队列中取出第一个节点，即$v_3$。
  • 根据给出的图发现，节点$v_3$的相邻节点有$v_1$和$v_6$。
    • 更新$v_1$和$v_6$的$visit$为$yes$，代表已经被访问过。更新$dist$为1（$v_3$到$v_1$的距离为1）。更新$path$为$v_3$。
    • 将$v_1$和$v_6$放入Queue队列中。
  • 进行第二轮循环

• Iteration 2

  • 从队列中取出第一个节点，即$v_1$。

  • 根据给出的图发现，节点$v_1$的相邻节点有$v_2$和$v_4$。

    • 更新$v_2$和$v_4$的$visit$为$yes$，代表已经被访问过。更新$dist$为1+1（$v_3$到$v_1$的距离为1，$v_1$到$v_2$的距离为1，因此为2）。更新$path$为$v_1$。
    • 将$v_2$和$v_4$放入Queue队列中。

  • 进行第三轮循环

• Iteration 3

  • 从队列中取出第一个节点，即$v_6$。

  • 根据给出的图发现，节点$v_6$没有相邻节点。不做操作。

  • 进行第四轮循环

• Iteration 4

  • 从队列中取出第一个节点，即$v_2$。

  • 根据给出的图发现，节点$v_2$的相邻节点有$v_4$和$v_5$。

    • 由于$v_4$已经被访问过了，不需要更新
    • 更新$v_5$的$visit$为$yes$，代表已经被访问过。更新$dist$为2+1。更新$path$为$v_2$。
    • 将$v_5$放入Queue队列中。

  • 进行五轮循环

• Iteration 5

  • 从队列中取出第一个节点，即$v_4$。

  • 根据给出的图发现，节点$v_4$的相邻节点有$v_3$、$v_5$、$v_6$和$v_7$。

    • 由于$v_3$、$v_5$和$v_6$已经被访问过了，不需要更新
    • 更新$v_7$的$visit$为$yes$，代表已经被访问过。更新$dist$为2+1。更新$path$为$v_4$。
    • 将$v_7$放入Queue队列中。

  • 判断Queue是否为空，若不为空，进行第六轮循环，若为空，则结束，Status table中记录了起点到其他所有节点的最短距离和路径。

• Iteration 6

  • 从队列中取出第一个节点，即$v_5$。

  • 根据给出的图发现，节点$v_5$的相邻节点有$v_7$。

    • 由于$v_7$已经被访问过了，不需要更新。

  • 判断Queue是否为空，若不为空，进行第七轮循环，若为空，则结束，Status table中记录了起点到其他所有节点的最短距离和路径。

• Iteration 7

  • 从队列中取出第一个节点，即$v_7$。

  • 根据给出的图发现，节点$v_7$的相邻节点有$v_6$。

    • 由于$v_6$已经被访问过了，不需要更新。

  • 判断Queue是否为空，若不为空，进行第八轮循环，若为空，则结束，Status table中记录了起点到其他所有节点的最短距离和路径。已经为空，结束。

通过上面的手算，我们理清了寻找有向无权图最短路径的算法步骤，有几个需要注意的地方用加粗标识出来。

算法实现

沿着上面的求解思路，我们不难得出，算法的结束标志就是队列是否为空，若为空，则代表算法结束。下面是我用python求解的代码，给一个图、起点和终点，得到最优路径。

import networkx as nx
import matplotlib.pyplot as plt
import math


#-------------------------------构建有向无权图-----------------------------------
# 创建无权有向图
Graph = nx.DiGraph()
# 添加节点
Graph.add_nodes_from(['v1', 'v2', 'v3', 'v4', 'v5', 'v6', 'v7'])
# 添加边
Graph.add_edges_from([
    ('v1', 'v2'),
    ('v1', 'v4'),
    ('v2', 'v4'),
    ('v2', 'v5'),
    ('v3', 'v1'),
    ('v3', 'v6'),
    ('v4', 'v3'),
    ('v4', 'v5'),
    ('v4', 'v6'),
    ('v4', 'v7'),
    ('v5', 'v7'),
    ('v7', 'v6'),
])
# 获取节点和边的数量
# print(list(Graph.edges))
# print(list(Graph.nodes))
# 画图
# nx.draw(Graph, pos=nx.planar_layout(Graph), with_labels=True)
# plt.show()



#-------------------------------寻找最短路径-----------------------------------
def find_shortest_path(Graph, begin_node, end_node):
    # 1. 初始化列表，用来存放节点
    select_nodes        = []
    neighboring_nodes   = []
    # 2. 初始化键值为列表的字典，存放访问信息
    total_nodes_status  = {}
    for node in Graph.nodes:
        total_nodes_status[node] = ['false', None, ' ']
        #print(total_nodes_status[node])
    # 3. 将起点插入selct_nodes
    select_nodes.append(begin_node)
    # 4. 更新total_nodes_status中的begin_node
    total_nodes_status[begin_node][0] = 'true'
    total_nodes_status[begin_node][1] = 0
    #print(total_nodes_status)
    # 5. 当select_nodes不为空时执行如下循环操作
    while(len(select_nodes)!=0):
        # 5.1 取出队列顶端的节点
        current_node = select_nodes[0]
        select_nodes.remove(current_node)
        # 5.2 找到current_node相邻的节点, 若该节点没有被访问过, 将其放入neighboring_nodes
        neighboring_nodes.clear()
        for node in Graph.neighbors(current_node):
            if total_nodes_status[node][0] == 'false':
                neighboring_nodes.append(node)
        # 5.3 对于neighboring_nodes中的所有节点，做下面操作
        for node in neighboring_nodes:
            # 5.3.1 将node插入select_nodes
            select_nodes.append(node)
            # 5.3.2 更新total_nodes_status中node被访问过
            total_nodes_status[node][0] = 'true'
            # 5.3.3 更新total_nodes_status中node的距离
            total_nodes_status[node][1] = total_nodes_status[current_node][1] + 1
            # 5.3.4 设置total_nodes_status中node的前置节点
            total_nodes_status[node][2] = current_node
    # 6. 若为空, 则执行完毕, 输出最终的状态
    for key, value in total_nodes_status.items():
        print(key, value)

    # 7.记录起点到终点的最优路径
    shortest_path = []
    shortest_path_length = total_nodes_status[end_node][1]
    current_node = end_node
    while current_node != begin_node:
        shortest_path.append(current_node)
        current_node            = total_nodes_status[current_node][2]
    shortest_path.append(begin_node)
    shortest_path.reverse()

    return shortest_path_length, shortest_path



#-------------------------------算例测试-----------------------------------
begin_node 	= 'v3'
end_node 	= 'v7'
shortest_path_length, shortest_path = find_shortest_path(Graph, begin_node, end_node)
print("起点%s到终点%s的最短距离是：%g \n "
      "路线如下所示：" % (begin_node, end_node, shortest_path_length))
path = ""
for element in shortest_path:
    if(element != end_node):
        path    += element
        path    += " -> "
    else:
        path    += element

print(path)

当我输入起点$v_3$和终点$v_7$时，运行算法，最终的Status table和最优路径如图所示：