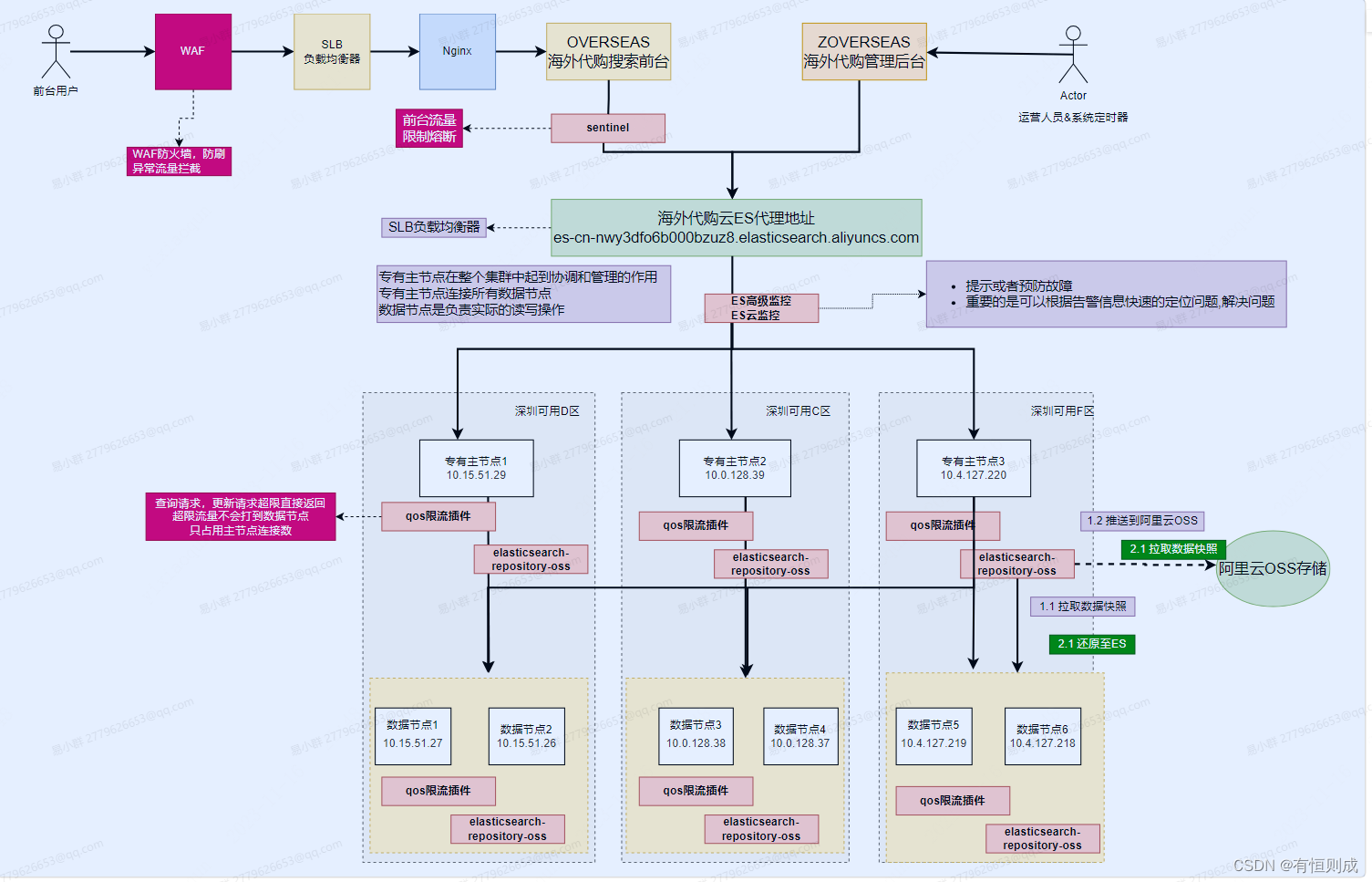
文章目录
- 邻接表
- 无向图
- 有向图
- 图的邻接表存储表示:
- 图的邻接表的弧(边)的结点结构
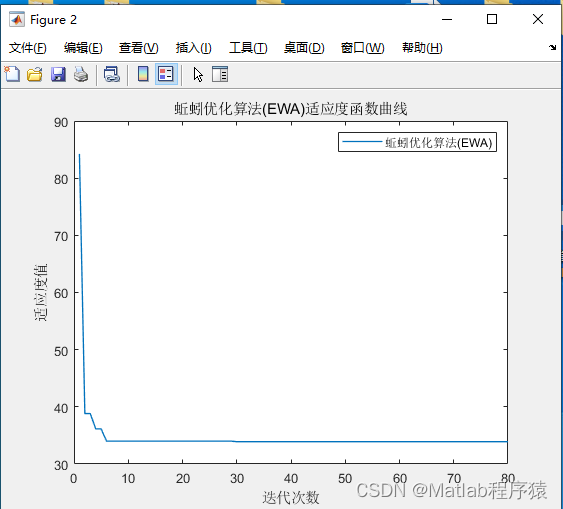
邻接矩阵的好处:
1.直观,简单,好理解。
2.方便检查任意一对顶点间是否存在边
3.方便找到任一顶点的所有“邻接点”(有边直接相连的顶点)。
4.方便计算任一顶点的“度”
- 无向图:对应行(列)非0元素的个数。
- 有向图:对应行非0元素的个数“出度”。
对应列的非0元素个数为“入度”。
邻接矩阵的缺点:
1.不便于增加和删除顶点。
2.浪费空间----存稀疏图(点很多而边很少)有大量无效元素。
但对稠密图(特别是完全图)还是很合算的。
3.浪费时间----统计稀疏图中一共有多少条边。
邻接表
无向图
1.邻接表表示法(链式)

头结点存储的是邻接点的序号和下一个顶点的地址域。

这里的adjvex是邻接点域:存放与vi邻接的顶点在表头数组中的位置。
nextarc:链域:指示下一条边或弧。
后面还可以加一个存储空间info:存储当前的权值。
- 顶点:
- 按编号顺序将顶点数据存储在一位数组中;
- 关联同一顶点的边(以顶点为尾的弧):
- 用线性链表存储。
邻接表的特点:
- 邻接表不唯一。
- 若无向图中有n个顶点,e条边,则其邻接表需n个头结点和2e个表结点。适宜存储稀疏图。
- 无向图中顶点vi的度为第i个单链表中的结点数。
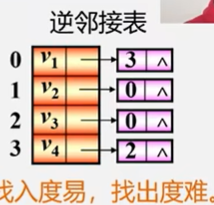
有向图
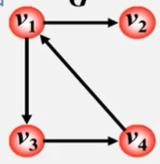
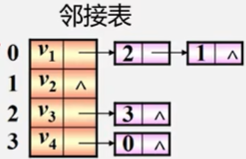
有向图只记录以v1为出度的顶点。
特点:
- 顶点vi的出度为第i个单链表中的结点数。
- 顶点vi的入度为整个单链表中邻接点域值是i-1的结点个数。
- 找出度易,找入度难。
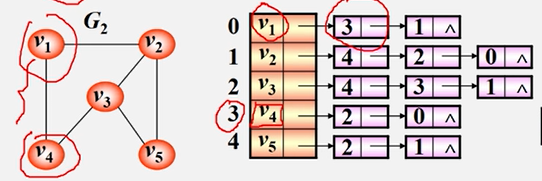
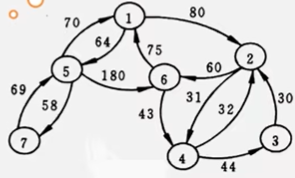
例:已知某网的邻接(出边)表,请画出该网络。
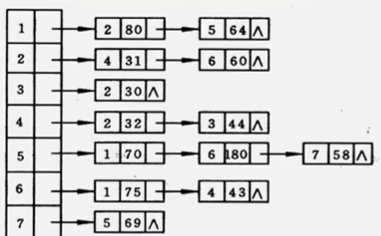
当邻接表的存储结构形成后,图便唯一确定。
图的邻接表存储表示:
typedef struct VNode {
VerTexType data;//顶点信息
ArcNode* firstarc;//指向第一条依附于顶点的边的指针
}VNode,AdjList[MVNum];//AdjList表示邻接表的类型
AdjList v:就是v里面的每一个变量都有数据和指针的两个部分; 相当于 VNode v[MVNum];
图的邻接表的弧(边)的结点结构

typedef struct ArcNode {//边结点
int adjvex;//该边所指向的顶点的位置
struct ArcNode* nextarc;//指向下一条边的指针
OtherInfo info;//和边相关的信息
}ArcNode;
图的结构定义:
typedef struct {
AdjList vertices;//邻接表类型的数组,存储着所有的结点
int vexnum, arcnum;//图的所有顶点和边(弧)
}ALGraph;
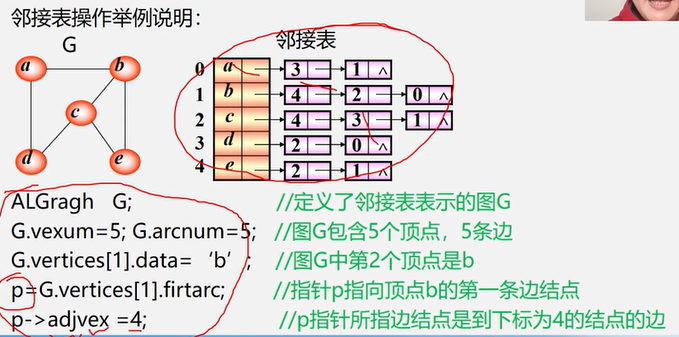
ALGraph G{};//定义了邻接表示的图G
G.vexnum = 5;
G.arcnum = 5;//定义了5个顶点,5条边
G.vertices[1].data = 'b';//图G的第二个顶点是b
p = G.vertices[1].firstarc;//指针p指向顶点b的第一条边的结点
p->adjvex = 4;//p指针所指结点是到下标为4的结点的边