目录

编码与调制

数字基带信号

模拟基带信号

码元

常用编码

不归零编码

归零编码 

曼彻斯特编码

差分曼彻斯特编码

编码习题

基本调制方法

调幅

调频

调相

混合调制

QAM-16

---

编码与调制

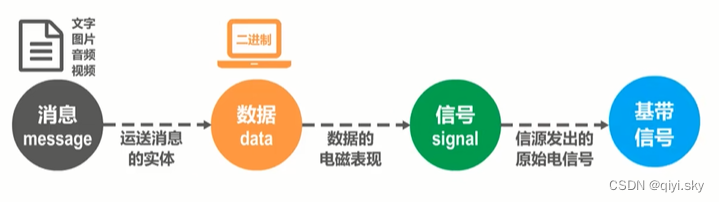
在计算机网络中，计算机需要处理和传输用户的文字、图片、音频和视频，他们可以统称为消息。

数据是运送消息的实体，我们人类比较熟悉的是十进制数据，而计算机只能处理二进制数据，也就是比特0和比特1。

计算机中的网卡，将比特0和比特1，变换成相应的电信号发送到网线。也就是说，信号是数据的电磁表现。

由信源发出的原始电信号，称为基带信号 。

基带信号又可分为两类：

• 一类是数字基带信号，例如计算机内部CPU与内存之间传输的信号。
• 另一类是模拟基带信号，例如麦克风收到声音后产生的音频信号。

数字基带信号

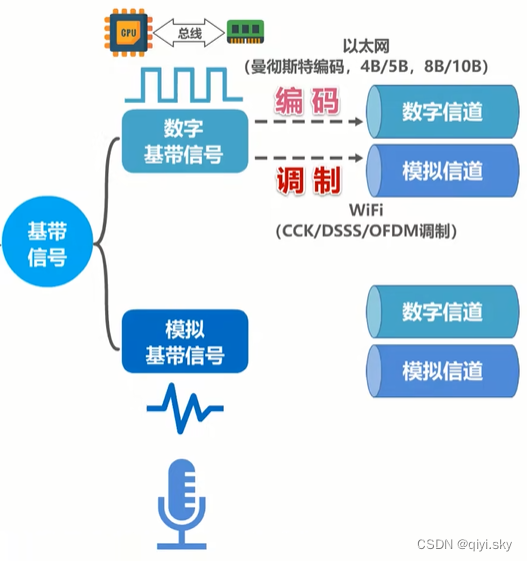
信号需要在信道中进行传输，信道可分为数字信道和模拟信道两种。

在不改变信号性质的前提下，仅对数字基带信号的波形进行变换，称为编码。

编码后产生的信号仍为数字信号，可以在数字信道中传输，例如以太网使用曼彻斯特编码，4B/5B，8B/10B等。

编码把数字基带信号的频率范围搬移到较高的频段，并转换为模拟信号，称为调制。

调制后产生的信号是模拟信号，可以在模拟信号中传输，例如Wifi使用补码键控，直接序列扩频，正交频分复用等调制方法。

模拟基带信号

对于模拟基带信号的处理，也有编码和调制两种方法。

对模拟基带信号进行编码的典型应用，是对音频信号进行编码的脉码调制PCM，也就是将模拟音频信号通过采样、量化、编码这三个步骤进行数字化。

对模拟信号进行调制的典型应用，是将语音数据加载到模拟的载波信号中传输。例如传统的电话。

另一个是频分复用FDM技术，可以充分利用带宽资源。

码元

接下来我们介绍码元的概念：

在使用时间域的波形表示数字信号时，代表不同离散数值的基本波形，称为码元。

简单来说，码元就是构成信号的一段波形。
例如这是一个调频信号：

图示这两段波形，是构成该信号的基本波形，我们可称其为码元。它们可以表示比特0，也可以表示比特1。

可见该信号由两种码元构成 。

注意传输媒体与信道的关系，

严格来说，传输媒体和信道不能直接划等号。

对于单工传输，传输媒体中只包含一个信道，要么是发送信道，要么是接收信道。

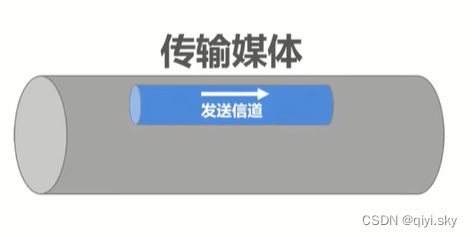
而对于半双工和全双工传输，传输媒体中要包含两个信道，一个是发送信道，另一个是接收信道。

如果使用信道复用技术，一条传输媒体还可以包含多个信道。 

在计算机网络中，常见的是将数字基带信号，通过编码或调制的方法在相应信道进行传输。

常用编码

下面介绍几种常用编码，这是待传输的比特流：

不归零编码

这是采用不归零编码产生的该比特流的相应信号，正电平表示比特1，负电平表示比特0。

这是零电平：

所谓不归零，就是指在整个码元时间内电平不会出现零电平。

例如该码元在其时间内全部是正电平

而该码元在其时间内全部是负电平

那么就有一个问题了：接收端如何判断出是两个码元还是三个码元。

这需要发送方的发送与接收方的接收做到严格的同步，需要额外一根传输线来传输时钟信号，接收方按时钟信号的节拍来逐个接收码元。

然而对于计算机网络，宁愿利用这根传输线来传输数据信号，而不是要传输时钟信号。

因此由于不归零编码存在同步问题，计算机网络中的数据传输不采用这类编码。

归零编码 

这是归零编码，分别有正电平、零电平、负电平：

很明显每个码元传输结束后，信号都要“归零”，所以接收方只要在信号归零后，进行采样即可，不需要单独的时钟信号。

实际上归零编码相当于把时钟信号用归零方式编码在了数据之内，这称为“自同步”信号。

但是归零编码中，大部分的数据带宽都用来传输归零而浪费掉了。

也就是说，归零编码的优点是自同步，但缺点是编码效率低。

曼彻斯特编码

这是曼彻斯特编码，如图所示

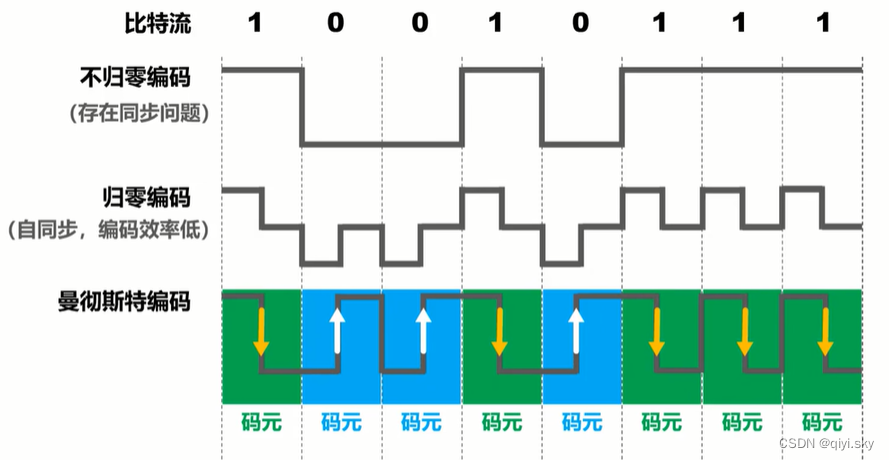
在每个码元时间的中间时刻，信号都会发生跳变；例如负跳变表示比特1，正跳变表示比特0。

码元中间时刻的跳变既表示时钟，又表示数据。

传统以太网使用的就是曼彻斯特编码。

差分曼彻斯特编码

这是差分曼彻斯特编码，如图所示

在每个码元时间的中间时刻，信号都会发生跳变。

与曼彻斯的编码不同，跳变仅表示时钟。

而用码元开始处电平是否发生变化，来表示数据，如图所示：

依据码元开始处电平是否发生变化，来表示比特0或比特1。

接下来我们做一个有关编码的练习题

编码习题

若下图为10BaseT网卡接收到的信号波形，则该网卡收到的比特串是：

A.0011 0110        B.1010 1101        C.0101 0010        D.1100 0101

10BaseT中的10表示带宽为10Mb/s，Base表示基带传输，T表示双绞线。

10BaseT这种以太网使用曼彻斯特编码。

根据曼彻斯特编码的特点，也就是每个码元在其中间时刻发生跳变，可以划分出所给信号中的各码元，至于正跳变表示1还是0，负跳变表示0还是1，没有具体规定，可以自行假设。

我们假设正跳变表示1，负跳变表示0，最终会发现没有一个答案是符合的，那说明我们的假设有错误。

那么应该是正跳变表示0，负跳变表示1，写出个码元所表示的比特，就很容易可以看出正确答案应为A。

下面介绍基本调制方法

基本调制方法

这是待传输的数字基带信号：

也就是来自信源的原始数字信号，我们要使用模拟信道来传输。

因此，需要将数字基带信号通过调制方法，调制成可以在模拟信道中传输的模拟信号。

调幅

这是调幅（AM）所产生的模拟信号：

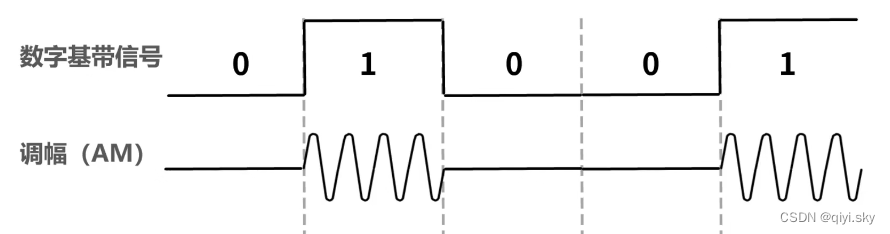
无载波输出，表示比特0；有载波输出，表示比特一 

调频

这是调频（FM）所产生的模拟信号：

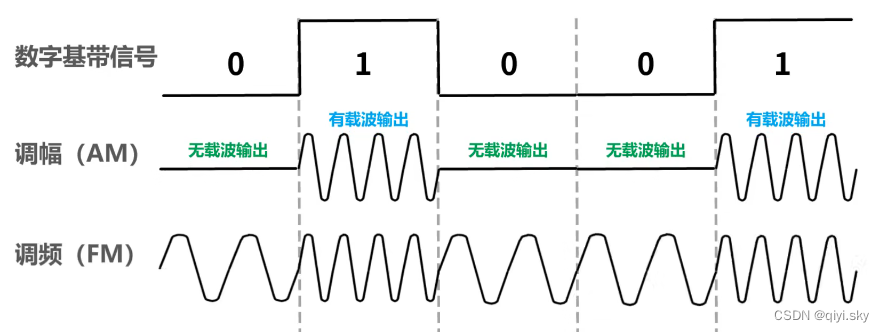
频率f1的波形表示比特0，频率f2的波形表示比特1

调相

这是调向（PM）所产生的模拟信号：

 初相位为0度的波形表示比特0；初相位为180度的波形表示比特1

很明显，使用基本调制方法，一个码元只能表示，或者说包含一个比特信息。
那么，如何能使一个码元包含更多的比特呢 ？

混合调制

可以采用混合调制的方法。

因为频率和相位是相关的，也就是说频率是相位随时间的变化率，所以一次只能调制频率和相位两个中的一个。

通常情况下，相位和振幅可以结合起来一起调制，称为正交振幅调制QAM。

QAM-16

我们来看属于正交振幅调制的QAM-16。

这种调制方法所调制出的波形，可以有12种相位，每种相位有一或两种振幅可选。
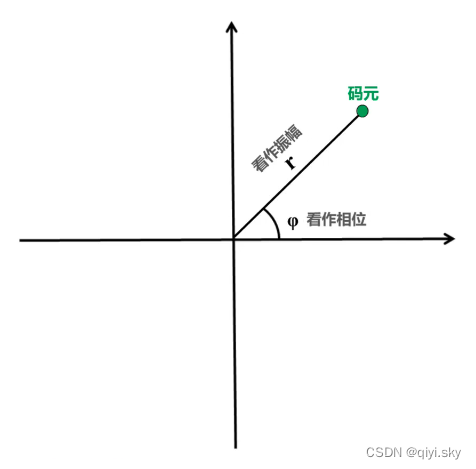
我们可在星座图中，画出该调制方法所产生的码元，该点就表示其中的一个码元：

它与圆心连线的距离可看作是振幅，连线与横坐标的夹角可看作是相位

这是QAM-16可调制出的16种码元：

思考两个问题：

•  每个码元可以包含几个比特
• 每个码元与4个比特的对应关系能否随便定义

如图所示，这是我们随便定义的每个码元所对应的4个比特：

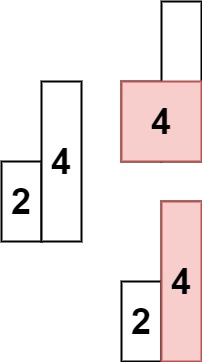
假设A B C D E是接收端接收到的5个码元，这5个码元原本都是表示4个比特0的：

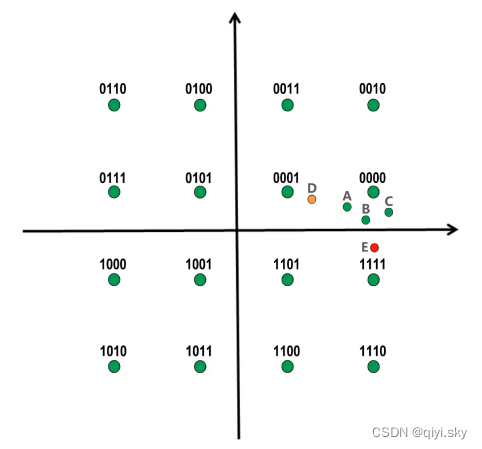
由于传输过程中产生失真，导致他们在星座图中并未落在理想的位置。

接收端可能会将码元A B C解调为0000，这是正确的；

也可能将码元D解调为0001，有一个错位；

也可能将码元E解调为1111，四位全错。

这就说明，每个码元与四个比特的对应关系，不能随便定义。

每个码元与4个比特的对应关系，应该采用格雷码，也就是任意两个相邻码元只有一个比特不同。

如图所示：

---

END 

---

学习自：湖科大——计算机网络微课堂