子串, 等价于 子数组, 都要求连续

回文子串

力扣链接

• 子串 ⇒ 状态表示
  

• 子串 ⇒ 状态转移方程
  

• 初始化 : 全都初始化为 false

• 遍历顺序
  

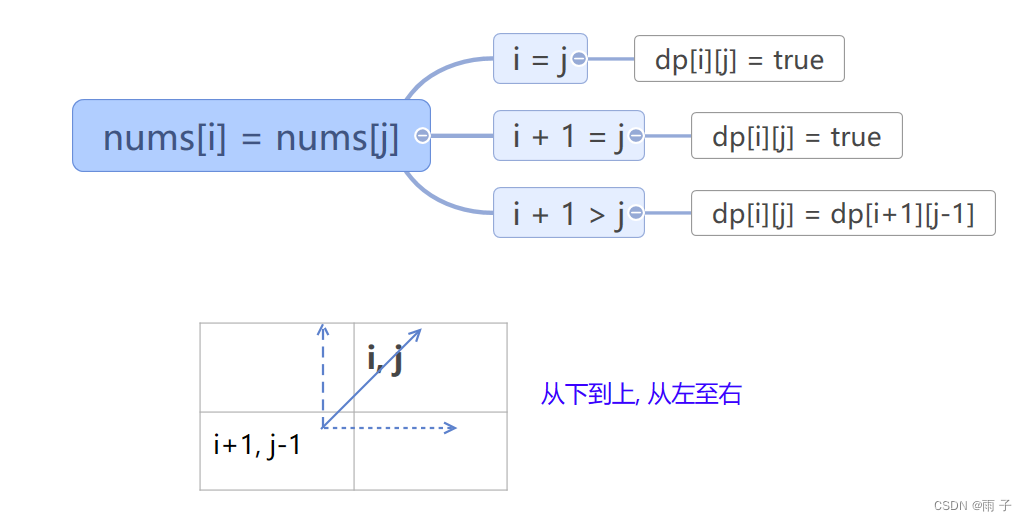
• 返回结果 : 此时的dp表中, 已经是每个区间能否是回文子串的结果了 ⇒ 我们要统计所有的回文子串的数目, 那么就是 统计dp表中为true的数量

class Solution {
public:
    int countSubstrings(string s) 
    {
        int n = s.size();

        // 建表 + 初始化
        vector<vector<bool>> dp(n, vector<bool>(n));

        // 统计结果
        int res = 0;

        for(int i = n-1; i >= 0; i--) // 固定起始位置
        {
            for(int j = i; j < n; j++) // 枚举结束位置
            {
                if(s[i] == s[j])
                {
                    if(i == j)  dp[i][j] = true;
                    else if(i+1 == j)  dp[i][j] = true;
                    else  dp[i][j] = dp[i+1][j-1];
                }

                // 统计dp表中为true的数量
                if(dp[i][j])  res++;
            }
        }

        return res;
    }
};

---

最长回文子串

力扣链接

• 子串 ⇒ 状态表示
  

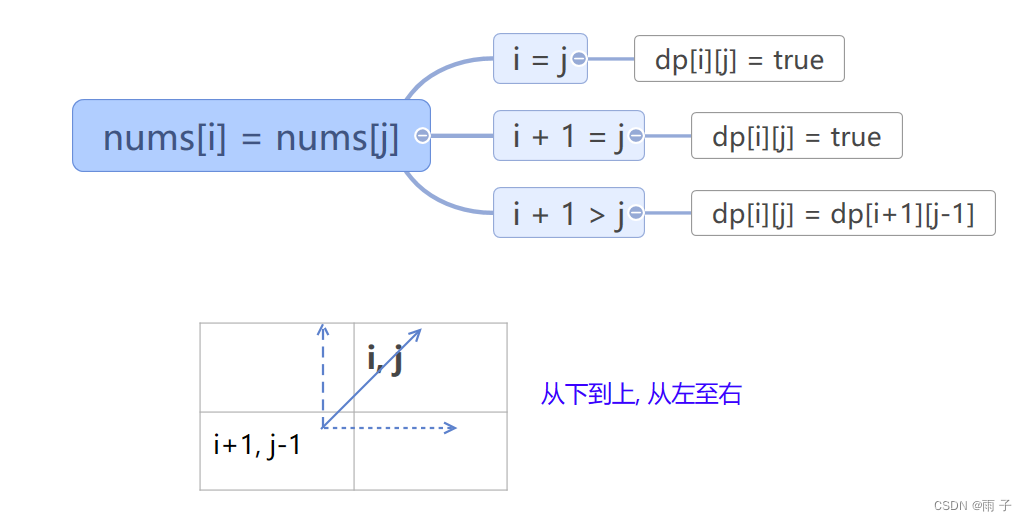
• 子串 ⇒ 状态转移方程
  

• 初始化 : 全都初始化为 false

• 遍历顺序
  

• 返回结果 : 记录最长长度 和 最长长度的起始下标 ⇒ substr

class Solution {
public:
    string longestPalindrome(string s) 
    {
        int n = s.size();

        // 建表 + 初始化
        vector<vector<bool>> dp(n, vector<bool>(n));

        // 返回结果
        int count = 0; // 记录最长长度
        int begin = 0; // 记录最长长度的起始下标

        // 填表
        for(int i = n-1; i >= 0; i--) // 固定起始下标
        {
            for(int j = i; j < n; j++) // 枚举结束下标
            {
                if(s[i] == s[j])
                {
                    if(i == j)  dp[i][j] = true;
                    else if(i+1 == j)  dp[i][j] = true;
                    else  dp[i][j] = dp[i+1][j-1];
                }

                // 更新最长长度 和 最长长度的起始下标
                if(dp[i][j] && j-i+1 > count)
                {
                    begin = i;
                    count = j-i+1;
                }
            }
        }

        // 返回结果
        string str = s.substr(begin, count);

        return str;
    }
};

---

铸镜须青铜，青铜易磨拭。结交远小人，小人难姑息。
铸镜图鉴微，结交图相依。凡铜不可照，小人多是非。
— — 孟郊《结交》