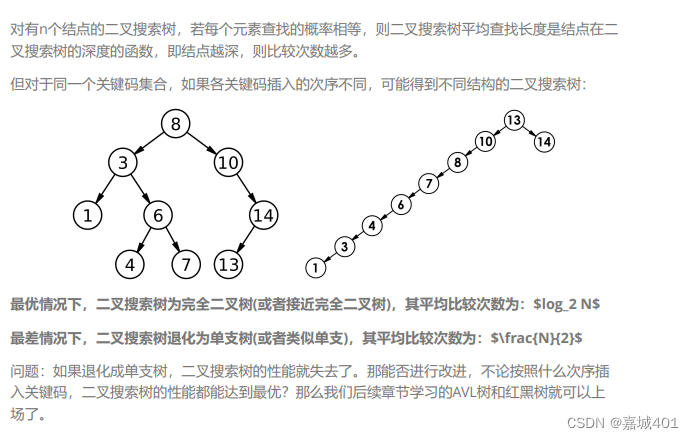
题目

84. 柱状图中最大的矩形

困难

相关标签

栈   数组   单调栈

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

示例 1:

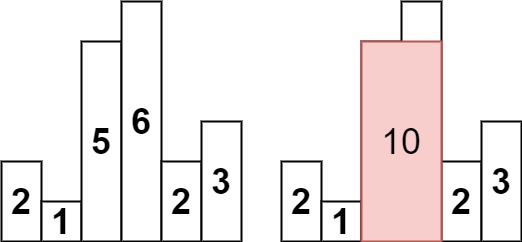
输入：heights = [2,1,5,6,2,3]
输出：10
解释：最大的矩形为图中红色区域，面积为 10

示例 2：

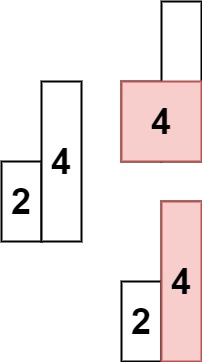
输入： heights = [2,4]
输出： 4

提示：

• 1 <= heights.length <=105
• 0 <= heights[i] <= 104

思路和解题方法

1. int result = 0;：初始化结果变量为0，用来存放最大矩形面积。
2. stack<int> st;：声明一个整型栈st，用来存放数组元素的下标。
3. heights.insert(heights.begin(), 0);：在heights数组头部插入一个值为0的元素。
4. heights.push_back(0);：在heights数组尾部插入一个值为0的元素。
5. st.push(0);：将0这个下标入栈。

接下来是for循环，遍历heights数组：

1. for (int i = 1; i < heights.size(); i++)：从下标1开始遍历heights数组。
2. if (heights[i] > heights[st.top()])：如果当前高度大于栈顶元素所对应的高度，则将当前下标入栈。
3. else if (heights[i] == heights[st.top()])：如果当前高度等于栈顶元素所对应的高度，则不做任何操作。
4. else：如果当前高度小于栈顶元素所对应的高度，进入循环。
5. while (!st.empty() && heights[i] < heights[st.top()])：当栈不为空且当前高度小于栈顶元素所对应的高度时，执行循环。
6. int mid = st.top(); st.pop();：取出栈顶元素的下标，并将其出栈。
7. if (!st.empty())：如果栈不为空，说明存在左边界。
8. int left = st.top(); int right = i;：获取左边界和右边界的下标。
9. int w = right - left - 1; int h = heights[mid];：计算矩形的宽度和高度。
10. result = max(result, w * h);：更新最大矩形面积。

最后，返回计算得到的最大矩形面积result。

复杂度

        时间复杂度:

                O(n)

时间复杂度为O(n)，其中n是输入数组heights的长度。因为在一次遍历中，每个元素最多被压入和弹出栈各一次，所以总的操作次数与输入数组的长度成线性关系。

        空间复杂度

                O(n)

空间复杂度为O(n)，主要是由栈st所使用的额外空间造成的。

c++ 代码

class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        int result = 0; // 初始化最大面积为0
        stack<int> st; // 定义一个栈来辅助计算
        heights.insert(heights.begin(), 0); // 数组头部加入元素0
        heights.push_back(0); // 数组尾部加入元素0
        st.push(0); // 将0入栈作为起始位置

        // 从下标1开始遍历数组
        for (int i = 1; i < heights.size(); i++) {
            if (heights[i] > heights[st.top()]) { // 情况一：当前高度大于栈顶高度，入栈
                st.push(i);
            } else if (heights[i] == heights[st.top()]) { // 情况二：当前高度等于栈顶高度，可以忽略
                st.pop(); // 这个可以加，可以不加，效果一样，思路不同
                st.push(i);
            } else { // 情况三：当前高度小于栈顶高度，需要计算面积并更新最大面积
                while (!st.empty() && heights[i] < heights[st.top()]) { // 注意是while
                    int mid = st.top(); // 弹出栈顶元素作为矩形的高度
                    st.pop();
                    if (!st.empty()) {
                        int left = st.top(); // 获取左边界
                        int right = i; // 获取右边界
                        int w = right - left - 1; // 计算宽度
                        int h = heights[mid]; // 获取高度
                        result = max(result, w * h); // 更新最大面积
                    }
                }
                st.push(i); // 将当前位置入栈
            }
        }
        return result; // 返回最大面积
    }
};

简洁代码

class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        stack<int> st; // 创建一个整型栈st，用来存放数组元素的下标
        heights.insert(heights.begin(), 0); // 在heights数组头部插入一个值为0的元素
        heights.push_back(0); // 在heights数组尾部插入一个值为0的元素
        st.push(0); // 将0这个下标入栈
        int result = 0; // 初始化结果变量为0，用来存放最大矩形面积
        for (int i = 1; i < heights.size(); i++) { // 遍历heights数组
            while (heights[i] < heights[st.top()]) { // 当当前高度小于栈顶元素所对应的高度时，执行循环
                int mid = st.top();
                st.pop(); // 取出栈顶元素的下标，并将其出栈
                int w = i - st.top() - 1; // 计算矩形的宽度
                int h = heights[mid]; // 获取矩形的高度
                result = max(result, w * h); // 更新最大矩形面积
            }
            st.push(i); // 将当前下标入栈
        }
        return result; // 返回计算得到的最大矩形面积
    }
};

Java代码

class Solution {
    public int largestRectangleArea(int[] heights) {
        // 创建一个新数组newHeight，长度比原数组heights多2，并在两端补0
        int[] newHeight = new int[heights.length + 2];
        System.arraycopy(heights, 0, newHeight, 1, heights.length); // 复制heights数组到newHeight数组
        newHeight[heights.length+1] = 0; // 在newHeight数组末尾加入一个值为0的元素
        newHeight[0] = 0; // 在newHeight数组头部加入一个值为0的元素

        Stack<Integer> stack = new Stack<>(); // 创建一个整型栈stack，用来存放数组元素的下标
        stack.push(0); // 将0这个下标入栈

        int res = 0; // 初始化结果变量为0，用来存放最大矩形面积
        for (int i = 1; i < newHeight.length; i++) { // 遍历newHeight数组
            while (newHeight[i] < newHeight[stack.peek()]) { // 当当前高度小于栈顶元素所对应的高度时，执行循环
                int mid = stack.pop(); // 取出栈顶元素的下标，并将其出栈
                int w = i - stack.peek() - 1; // 计算矩形的宽度
                int h = newHeight[mid]; // 获取矩形的高度
                res = Math.max(res, w * h); // 更新最大矩形面积
            }
            stack.push(i); // 将当前下标入栈
        }
        return res; // 返回计算得到的最大矩形面积
    }
}

觉得有用的话可以点点赞，支持一下。

如果愿意的话关注一下。会对你有更多的帮助。

每天都会不定时更新哦  >人<  。