✏️✏️✏️今天给大家分享几道二叉树OJ题!
😛😛😛希望我的文章能对你有所帮助,有不足的地方还请各位看官多多指教,大家一起学习交流!
动动你们发财的小手,点点关注点点赞!在此谢过啦!哈哈哈!😛😛😛
✏️✏️✏️如果觉得我分享和内容还不错的话,可以给我一个小小的赞吗
清风的CSDN博客

目录
一、检查两棵树是否相同
二、另一棵树的子树
三、翻转二叉树
四、平衡二叉树的判断
五、对称二叉树
一、检查两棵树是否相同
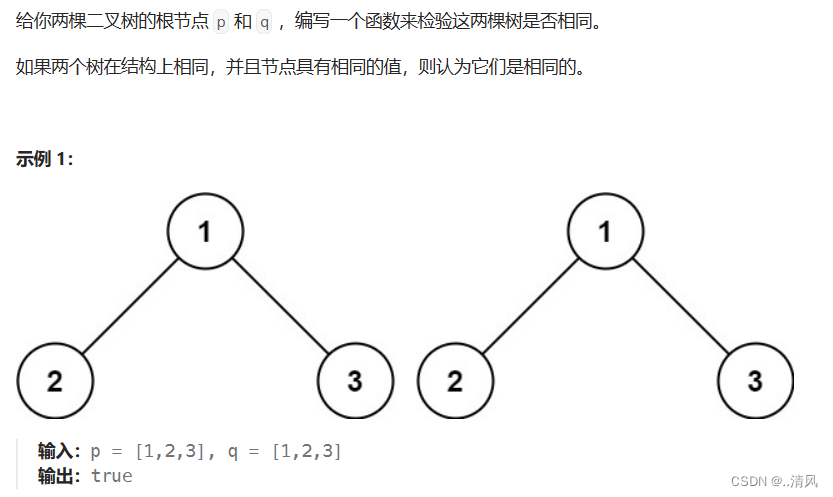
两个二叉树相同,当且仅当两个二叉树的结构完全相同,且所有对应节点的值相同。因此,可以通过搜索的方式判断两个二叉树是否相同。
思路:
- 如果两个二叉树都为空,则两个二叉树相同。如果两个二叉树中有且只有一个为空,则两个二叉树一定不相同。
-
如果两个二叉树都不为空,那么首先判断它们的根节点的值是否相同。
-
若不相同则两个二叉树一定不同。
-
若相同,再分别判断两个二叉树的左子树是否相同以及右子树是否相同。
-
这是一个递归的过程,因此可以使用深度优先搜索,递归地判断两个二叉树是否相同。
class Solution {
public boolean isSameTree(TreeNode p, TreeNode q) {
if((p==null && q!=null) || (p!=null && q==null)){
return false;
}
if(p==null && q==null){
return true;
}
//走到这里,p和q都不为空
if(p.val!=q.val){
return false;
}
return isSameTree(p.left,q.left) && isSameTree(p.right,q.right);
}
}二、另一棵树的子树
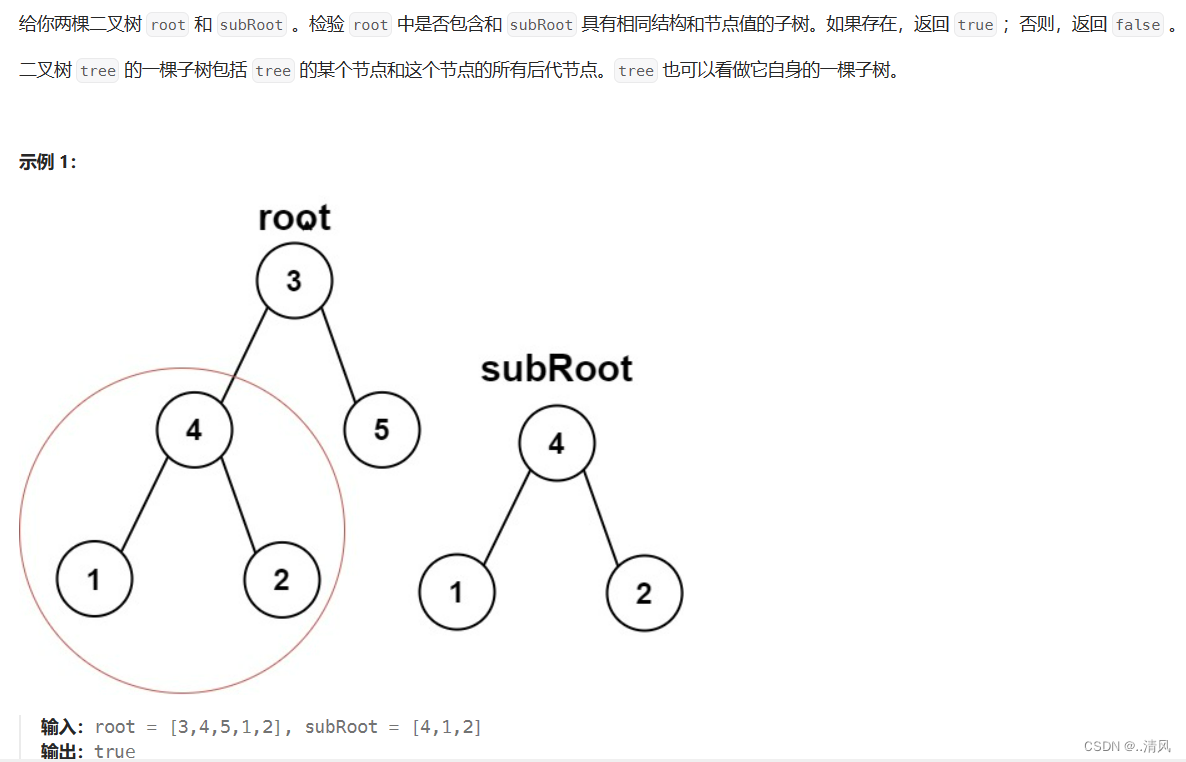
思路:
- 首先可以想到,如果两棵树都为空,那么直接返回false就可以了。
- 其次可以判断,题目所给的两棵树是否相同,如果相同,也满足条件,返回true。而判断两棵树相同,又需要深度优先搜索,这里就可以利用上面那道题的判断两棵树相同的思路,进行判断。
- 如果两棵树不相同,那么就把题目所给的子树分别和另一棵树的左子树比较,右子树比较。
- 可以通过递归的方式去进行深度优先搜索。
class Solution {
public boolean isSubtree(TreeNode root, TreeNode subRoot) {
if(root==null && subRoot==null){
return false;
}
if(isSameTree(root,subRoot)){
return true;
}
if(root==null){
return false;
}
if(isSubtree(root.left,subRoot)){
return true;
}
if(isSubtree(root.right,subRoot)){
return true;
}
return false;
}
public boolean isSameTree(TreeNode p, TreeNode q) {
if((p==null && q!=null) || (p!=null && q==null)){
return false;
}
if(p==null && q==null){
return true;
}
//走到这里,p和q都不为空
if(p.val!=q.val){
return false;
}
return isSameTree(p.left,q.left) && isSameTree(p.right,q.right);
}
}三、翻转二叉树

思路:
-
从根节点开始,递归地对树进行遍历。
-
从根的左右节点先开始翻转。翻转其实就是交换节点的引用。交换完根的左右节点之后,递归的进行翻转左子树和右子树即可。
-
每次翻转后,先判断翻转后的节点的next域是否为null,若为null则无需进行再次翻转。也相当于是一个小小的优化。
class Solution { public TreeNode invertTree(TreeNode root) { if(root==null){ return null; } TreeNode tmp=root.left; root.left=root.right; root.right=tmp; if(root.left==null && root.right==null){ return root; } invertTree(root.left); invertTree(root.right); return root; } }四、平衡二叉树的判断

思路:
- 一棵二叉树是平衡二叉树,当且仅当其所有子树也都是平衡二叉树,因此可以使用递归的方式判断二叉树是不是平衡二叉树,递归的顺序可以是自顶向下或者自底向上。
- 用递归的方式判断二叉树是不是平衡二叉树,其实就是左子树个右子树的高度差的绝对值是否小于等于1。
- 那么只需要递归的判断二叉树的左右子树的高度差的绝对值是否不大于1即可。
- 可以定义一个求高度的方法,当在递归调用这个方法的过程中,若发现左右子树的高度差大于1时,直接返回-1,则不需要在进行递归遍历,减少递归次数。
class Solution {
public boolean isBalanced(TreeNode root) {
if(root==null){
return true;
}
return height(root)>0;
}
private int height(TreeNode root){
if(root==null){
return 0;
}
int leftHeight=height(root.left);
if(leftHeight<0){
return -1;
}
int rightHeight=height(root.right);
if(leftHeight>=0 && rightHeight>=0 && Math.abs(leftHeight-rightHeight)<=1){
return Math.max(leftHeight,rightHeight)+1;
}else{
return -1;
}
}
}五、对称二叉树
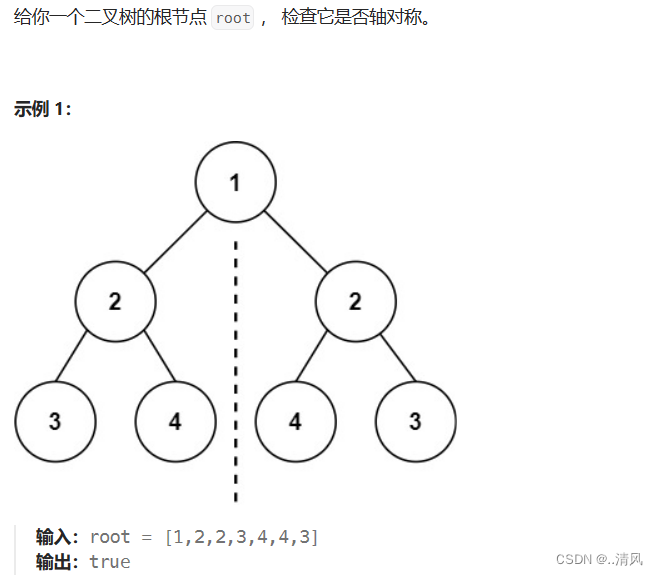
思路:
-
如果一个树的左子树与右子树镜像对称,那么这个树是对称的。
-
要判断树的左子树与右子树对称,首先一个为空一个不为空的情况,那么一定是不对称的。其次,判断左子树的根和右子树的根的值是否一样,以及左树的左和右树的右、左树的右和右树的左是否相同,利用递归的方式进行判断即可。
class Solution {
public boolean isSymmetric(TreeNode root) {
if(root==null){
return true;
}
return isSymmetree(root.left,root.right);
}
public boolean isSymmetree(TreeNode lefttree,TreeNode righttree){
if((lefttree!=null&&righttree==null) || (lefttree==null&&righttree!=null)){
return false;
}
if(lefttree==null && righttree==null){
return true;
}
if(lefttree.val!=righttree.val){
return false;
}
return isSymmetree(lefttree.right,righttree.left) &&
isSymmetree(lefttree.left,righttree.right);
}
}
✨希望各位看官读完文章后,能够有所提升。
🎉好啦,今天的分享就到这里!!
✨创作不易,还希望各位大佬支持一下!
👍点赞,你的认可是我创作的动力!
⭐收藏,你的青睐是我努力的方向!
✏️评论:你的意见是我进步的财富