[PyTorch][chapter 63][强化学习-QLearning]

news2024/11/26 4:29:32

前言：

这里结合走迷宫的例子,重点学习一下QLearning迭代更新算法

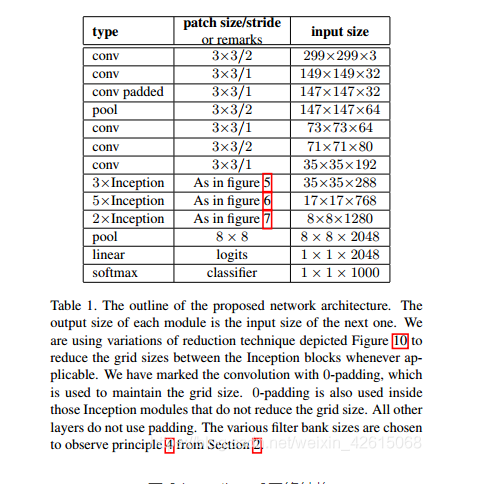
0,1,2,3,4 是房间，之间绿色的是代表可以走过去。

5为出口

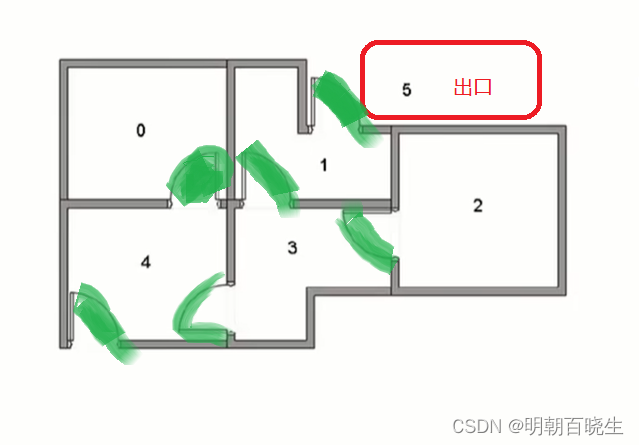
可以用下图表示

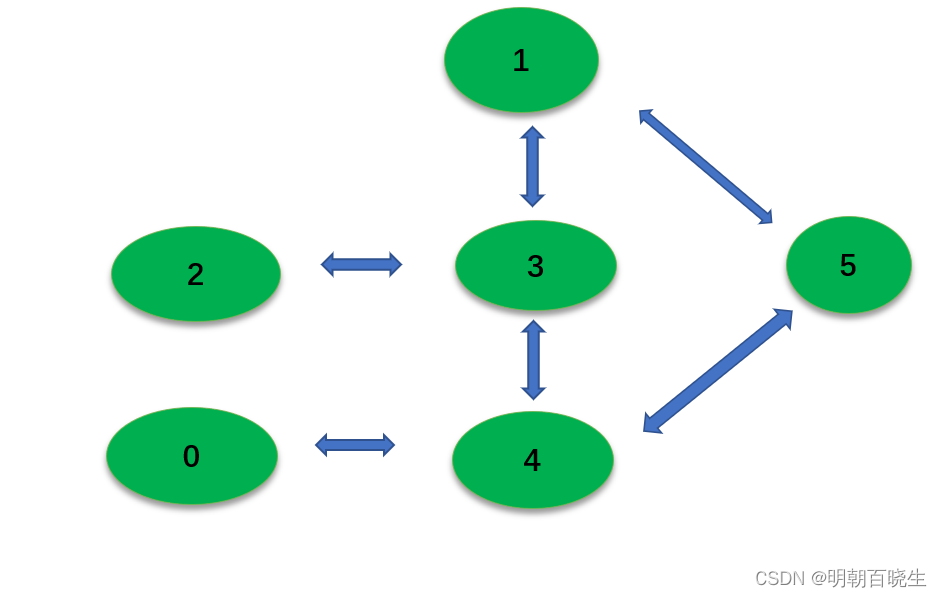
目录：

策略评估
策略改进
迭代算法
走迷宫实现Python

一策略评估

强化学习最终是为了学习好的策略 $\pi$ ，在不同的state 下面根据策略 $\pi$ 做出最优的action.

对于策略评估我们通过价值函数来度量.

1.1 状态值函数 V

T步累积奖赏: $V_{T}^{\pi}(s)=E_{\pi}[\frac{1}{T}\sum_{t=1}^{T}r_t|s_0=s]$ ,

$\gamma$ 折扣累积奖赏: $V_{\gamma}^{\pi}(s)=E_{\pi}[\sum_{t=0}^{\infty }\gamma^tr_{t+1}|s_0=s]$

1.2 状态-动作值函数 Q

T步累积奖赏: $Q_{T}^{\pi}(s,a)=E_{\pi}[\frac{1}{T}\sum_{t=1}^{T}r_t|s_0=s,a_0=a]$ ,

$\gamma$ 折扣累积奖赏: $V_{\gamma}^{\pi}(s,a)=E_{\pi}[\sum_{t=0}^{\infty }\gamma^tr_{t+1}|s_0=s,a_0=a]$

1.3 Bellan 等式展开

状态值函数 V

$V_{T}^{\pi}(s)=\sum_{a \in A} \pi(s,a) \sum_{s^{'} \in S}P_{s\rightarrow s^{'}}^a(\frac{1}{T}R_{s \rightarrow s^{'}}^{a}+\frac{T-1}{T}V_{T-1}^{\pi}(s^{'}))$

$V_{\gamma}^{\pi}(s)=\sum_{a \in A} \pi(s,a) \sum_{s^{'} \in S}P_{s\rightarrow s^{'}}^a(R_{s \rightarrow s^{'}}^{a}+\gamma V_{\gamma}^{\pi}(s^{'}))$

状态-动作函数Q

$Q_{T}^{\pi}(s,a)=\sum_{s^{'} \in S}P_{s\rightarrow s^{'}}^a(\frac{1}{T}R_{s \rightarrow s^{'}}^{a}+\frac{T-1}{T}V_{T-1}^{\pi}(s^{'}))$

$Q_{\gamma}^{\pi}(s,a)=\sum_{s^{'} \in S}P_{s\rightarrow s^{'}}^a(R_{s \rightarrow s^{'}}^{a}+\gamma V_{\gamma}^{\pi}(s^{'}))$

二策略改进

强化学习的目的：尝试各种策略 $\pi$ ，找到值函数最大的策略（累积奖赏）

$\pi^{*}= argmax_{\pi} \sum_{s \in S} V^{\pi}(s)$

2.1 最优策略值函数

$\forall s \in S :$ $v^{*}(s)=V^{\pi^{*}}(s)$

由于最优值函数的累积奖赏已经达到最大值,因此可以对Bellman 等式做个改动，即对动作求和改为最优

$V_{T}^{*}(s)=max_{a\in A} \sum_{s^{'} \in S}P_{s\rightarrow s^{'}}^a(\frac{1}{T}R_{s \rightarrow s^{'}}^{a}+\frac{T-1}{T}V_{T-1}^{*}(s^{'}))$ ..1

$V_{\gamma}^{*}(s)=max_{a\in A}\sum_{s^{'} \in S}P_{s\rightarrow s^{'}}^a(R_{s \rightarrow s^{'}}^{a}+\gamma V_{\gamma}^{\pi}(s^{'}))$ ...2

则

$V^{*}(s)= max_{a \in A} Q^{\pi^{*}}(s,a)$ ...3

最优状态-动作 Bellman 等式为：

$Q_{T}^{*}(s,a)= \sum_{s^{'} \in S}P_{s\rightarrow s^{'}}^a(\frac{1}{T}R_{s \rightarrow s^{'}}^{a}+\frac{T-1}{T} max_{a^{'} \in A}Q_{T-1}^{*}(s^{'},a^{'}))$

$V_{\gamma}^{*}(s,a)=\sum_{s^{'} \in S}P_{s\rightarrow s^{'}}^a(R_{s \rightarrow s^{'}}^{a}+\gamma max_{a^{'} \in A}Q_{\gamma}^{*}(s^{'},a^{'}))$

三递推改进方式

原始策略为 $\pi$

改进后策略 $\pi^{'}$

改变动作的条件为： $V^{\pi}(s) \leq Q^{\pi}(s,\pi^{'}(s))$

$V^{\pi}(s) \leq Q^{\pi}(s,\pi^{'}(s))$

$=\sum_{s^{'} \in S}P_{s\rightarrow s^{'}}^{\pi^{'}(s)}(R_{s \rightarrow s^{'}}^{\pi^{'}(s)}+\gamma V^{\pi}(s^{'}))$

$\leq \sum_{s^{'} \in S}P_{s\rightarrow s^{'}}^{\pi^{'}(s)}(R_{s \rightarrow s^{'}}^{\pi^{'}(s)}+\gamma Q^{\pi}(s^{'},\pi^{'}(s^{'})))$

...

$=V^{\pi^{'}}(s)$

四值迭代算法

4.1 环境变量

Reward 和 QTable 都是矩阵

4.2 迭代过程

当state 为1,Q 函数更新过程

5.3 收敛结果

五 走迷宫实现Python
reward 我们用一个矩阵表示：

行代表： state

列代表： action

值代表： reward

5.1 Environment.py 实现环境功能

# -*- coding: utf-8 -*-
"""
Created on Wed Nov 15 11:12:13 2023

@author: chengxf2
"""

import numpy as np
from enum  import Enum

#print(Weekday.test.value) 房间
class Room(Enum):
    
      room1 = 1
      room2 = 2
      room3 = 3
      room4 = 4
      room5 = 5
      
      



class Environment():
    
    def action_name(self, action):
        
        if action ==0:
            name = "左"
        elif action ==1:
            name = "上"
        elif action ==2:
            name = "右"
        else:
            name = "上"
        return name
    
    def __init__(self):
        
        
         
         self.R =np.array([ [-1, -1, -1, -1,  0, -1],
                   [-1, -1, -1,  0, -1, 100],
                   [-1, -1, -1,  0, -1, -1],
                   [-1,  0,  0, -1,  0, -1],
                   [0,  -1, -1,  0, -1, 100],
                   [-1,  0, -1, -1,  0, 100]])
         
         
    
    def step(self, state, action):
        #即使奖励： 在state, 执行action, 转移新的 next_state,得到的即使奖励
        #print("\n step ",state, action)
        reward = self.R[state, action]
        next_state = action# action 网哪个房间走
        if action == Room.room5.value:
            
            done = True
        else:
            done = False
        
    
        return  next_state, reward,done

5.1 main.py 实现Agent 功能

# -*- coding: utf-8 -*-
"""
Created on Wed Nov 15 11:29:14 2023

@author: chengxf2
"""

# -*- coding: utf-8 -*-
"""
Created on Mon Nov 13 09:39:37 2023

@author: chengxf2
"""

import numpy as np

def init_state(WORLD_SIZE):
    
    S =[]
    for i in range(WORLD_SIZE):
        for j in range(WORLD_SIZE):
            
            state =[i,j]
            S.append(state) 
            
    print(S)
    
# -*- coding: utf-8 -*-
"""
Created on Fri Nov 10 16:48:16 2023

@author: chengxf2
"""

import numpy as np
from environment  import Environment


class Agent():
    
    def __init__(self,env):
        self.discount_factor = 0.8 #折扣率
        self.theta = 1e-3 #最大偏差
        self.nS = 6 #状态 个数
        self.nA=  6  #动作个数
        self.Q = np.zeros((6,6))
        self.env = env
        self.episode = 500
       
        
    
    
    #当前处于的位置,V 累积奖赏
    def one_step_lookahead(self,env, state, action):
        
        #print("\n state :",state, "\t action ",action)
        next_state, reward,done = env.step(state, action)
        
        maxQ_sa = max(self.Q[next_state,:])
        
        return next_state, reward, done,maxQ_sa
        

    
    def value_iteration(self, env, state, discount_factor =1.0):
        
         #随机选择一个action,但是不能为-1
         
         indices = np.where(env.R[state] >-1)[0]
         action =  np.random.choice(indices,1)[0]
         #print("\n state :",state, "\t action ",action)
         next_state, reward, done,maxQ_sa = self.one_step_lookahead(env, state, action)
         
         #更新当前的Q值
         
         r  = reward + self.discount_factor*maxQ_sa
         
         self.Q[state,action] = int(r)
         
         #未达到目标状态，走到房间5， 执行下一次迭代
         if done == False:
             
             self.value_iteration(env, next_state)
             
         

    def learn(self):

        
        for n in range(self.episode): #最大迭代次数
            
            #随机选择一个状态
            state = np.random.randint(0,self.nS)
            
            #必须达到目标状态，跳转到出口房间5
            self.value_iteration(env, state, discount_factor= self.discount_factor)
            #print("\n n ",n)
        print(self.Q)
        
            
if __name__ == "__main__":
    
    env = Environment()
    agent =Agent(env)
    agent.learn()

参考：

8-QLearning基本原理_哔哩哔哩_bilibili

9-QLearning迭代计算实例_哔哩哔哩_bilibili

10-QLearning效果演示_哔哩哔哩_bilibili

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1213655.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！