文章目录
- 前言
- 人工智能 :一种现代的方法 第七章 逻辑智能体
- 7.1 基于知识的智能体
- 7.2 Wumpus世界
- 7.4 命题逻辑
- 7.5 命题逻辑定理证明
- 7.5.1推导和证明
- 7.5.2 归结原理
- 7.5.3 horn子句和限定子句
- 7.5.4 前向链接和后向链接
- 7.6 有效命题逻辑模型求解
- 7.6.1完备的回溯算法
- 7.6.2 不完备的回溯算法
- 7.7 基于命题逻辑的Agent
- 7.7.1 世界的当前状态
前言
本文旨在讲清楚:
- KBA(knowledge based agent)与逻辑
- 模型,有效性,可满足性,蕴含,推理过程
- 如何证明KB蕴含a(模型检验,逻辑等价,推理规则)
- 基于命题逻辑的Agent如何工作的
人工智能 :一种现代的方法 第七章 逻辑智能体
7.1 基于知识的智能体
基于知识的系统
def KB_AGENT(percept):
# 定义持久化变量
persistent KB, t
counter = 0 # 初始时间为0
# 告知知识库当前感知到的信息
Tell(KB, MAKE_PERCEPT_SENTENCE(percept, t))
# 提出询问
action = ASK(KB, MAKE_ACTION_QUERY())
# 告知知识库当前执行的动作
Tell(KB, MAKE_ACTION_SENTENCE(action, t))
t += 1 # 时间步进
return action
基于知识的Agent的核心部件是其知识库,或称KB。
知识库(KB):是一个语句(用知识表示语言表达,表示了关于世界的某些断言)集合。有时,当某语句是直接给定而不是推导得到的时候,我们将其尊称为公理。
Ask:查询目前所知内容
Tell:将新语句添加到知识库
KBA(Knowledge based agent),即基于知识的Agent,通过感知器,把感知信息加入知识库,向知识库询问最好改采取哪个行动,并告诉知识库它会实施该行动。
以基于知识的旅行规划助手为例

- 知识表示:旅行知识库可以使用图谱或本体表示来存储城市、景点、交通路线等信息。图谱可以表示城市之间的关系、景点之间的关联,本体可以定义旅行相关的概念和属性。
- 知识获取:旅行知识可以通过多种途径获取,包括从旅游网站、旅游指南、用户评论等抽取数据,并将其转化为可用的知识表示形式。
用户输入处理:系统需要解析用户提供的旅行起点、终点,以及偏好和时间限制等信息。 - 知识推理:系统可以利用推理技术从旅行知识库中提取有用的信息。例如,通过图谱的关系和规则的逻辑推理,找到连接起点和终点的最佳路线;通过用户偏好和景点属性的匹配,筛选出符合用户偏好的景点。
- 结果生成:根据推理的结果,系统可以生成旅行规划建议,包括路线、景点选择、交通方式等。这些建议可以按照用户的偏好和时间限制进行排序和过滤。
- 用户交互:系统可以提供用户界面,让用户查看和选择旅行规划建议。用户可以与系统进行交互,提供反馈和调整,系统也可以根据用户的反馈进行进一步的推荐和优化。
最重要的是知识表示和知识推理(本章节是以命题逻辑为例,是最基础的表示方法)
7.2 Wumpus世界
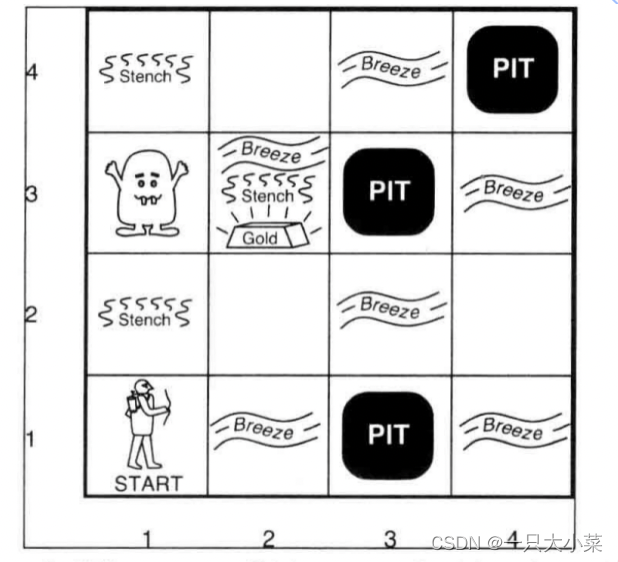
Wumpus世界是由多个房间组成并相连接起来的山洞;
- 某处隐藏着一只Wumpus怪兽,会吃掉进入它房间的任何人;
- Agent可以射杀Wumpus,但只有一支箭;
- 某些房间是无底洞,任何人进入这些房间会被无底洞吞噬;
- 生活在该环境的唯一希望是发现一堆金子。
在与无底洞相邻的方格内,Agent能感知到微风;
在与Wumpus相邻的方格内,Agent能感受到臭气;
在金子所处方格,Agent能感受到闪闪金光;
当Agent碰到墙时,它感知到碰撞;
当Wumpus被杀死后,它发出的嚎叫声在洞穴(所有房间组成一个山洞)内的任何地方都能感受到;
问题定义(PEAS):
- 性能度量:带着金子爬出洞口+1000;掉入无底洞或被Wumpus吃掉-1000;采取一个行动-1;用掉箭-10;Agent死亡或Agent出洞,游戏结束。
- 环境:4*4的房间网格。Agent从(1,1)出发,面向右方。金子和Wumpus、无底洞随机选择在除了起始方格的任一方格;
- 执行器:Agent可以向前、左转、右转。可以捡起所处方格内的物体;可以向正对方向射箭;箭向前运动直到击中Wumpus;Agent只能从(1,1)中爬出。
- 传感器:有5个传感器[臭气,微风,金光,撞击,嚎叫]例:[Stench, Breeze, None, None, None]
环境情况
环境情况:离散的、静态的、单个Agent、部分可观察的;
7.4 命题逻辑
基本语法
原子语句:单个命题词组成,每个命题词代表一个真或假的命题
复合句:简单语句和逻辑连接词构造而成
文字:原子命题及其否定。
互补文字:一个文字是另一文字的否定。
子句:文字的析取式。单个文字可以被视为只有一个文字的析取式,也叫单元子句。
合取范式公式:若干子句的合取
归并:去除文字的多余副本。
5种常用逻辑连接词:
1)非 ¬,否定式
2)与 ∧,合取式
3)或 ∨,析取式
4)蕴含 ⇒或→或⊃,蕴含式
蕴含式也称为规则或if-then语句。
5)当且仅当 ⇔(英文:If and only if, 或者:iff),双向蕴含式
一个简单的知识库

简单的推理过程
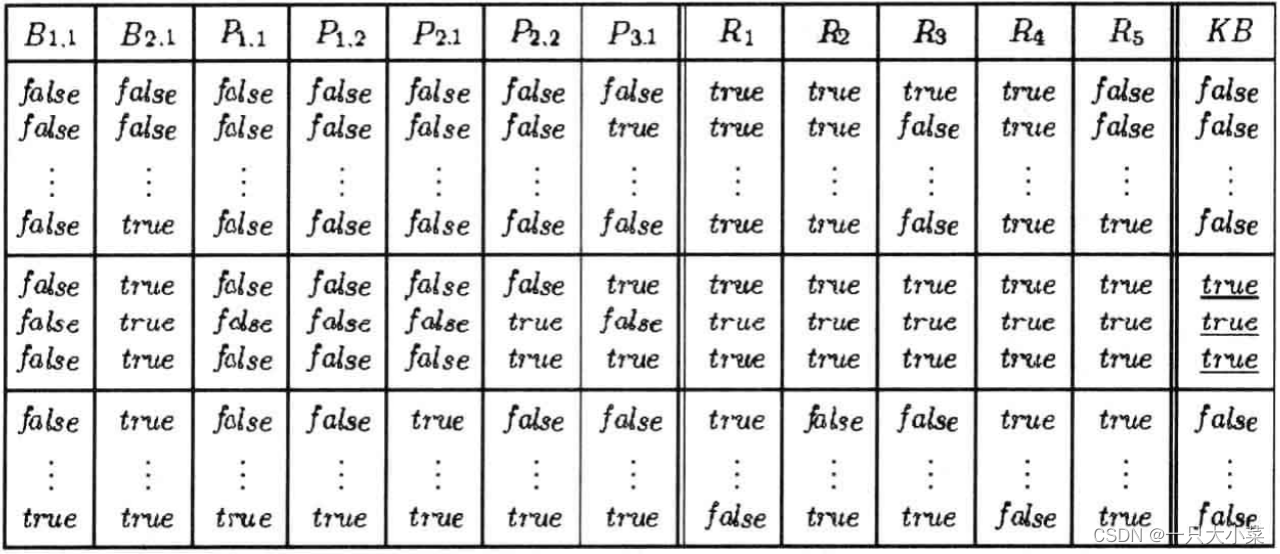
递归蕴含算法
def TT_ENTAILS(KB, a):
# 获取KB和a中的命题符号列表
symbols = get_proposition_symbols(KB, a)
return TT_CHECK_ALL(KB, a, symbols, {})
def TT_CHECK_ALL(KB, a, symbols, model):
if not symbols:
if PL_TRUE(KB, model):
return PL_TRUE(a, model)
else:
return True # 当KB为假时,总是返回True
else:
P = symbols[0]
rest = symbols[1:]
return (TT_CHECK_ALL(KB, a, rest, extend_model(model, P, True)) and
TT_CHECK_ALL(KB, a, rest, extend_model(model, P, False)))
# 获取KB和a中的命题符号列表
def get_proposition_symbols(KB, a):
symbols = set()
symbols.update(get_symbols(KB))
symbols.update(get_symbols(a))
return list(symbols)
# 获取句子中的命题符号列表
def get_symbols(sentence):
symbols = []
# 实现获取命题符号的逻辑
return symbols
# 将命题符号与取值扩展到模型中
def extend_model(model, symbol, value):
model_extended = model.copy()
model_extended[symbol] = value
return model_extended
# 判断句子在给定模型下是否为真
def PL_TRUE(sentence, model):
# 返回句子在给定模型下的真值结果
return True or False # 根据实际情况进行实现
7.5 命题逻辑定理证明
7.5.1推导和证明
推导规则:
1)假言推理规则(Modus Ponens,拉丁文):
α
⇒
β
,
α
β
\frac{\alpha \Rightarrow \beta , \alpha}{\beta}
βα⇒β,α
2)消去合取词 :
α
∧
β
α
\frac{\alpha \wedge \beta}{\alpha}
αα∧β
3)逻辑等价:如果两个语句在同样的模型集合中为真,则二者逻辑等价。
任意搜索算法来找出证明序列,只需定义如下证明问题:
- 初始状态:初始KB
- 行动:行动集合由应用于语句的所有推理规则组成
- 结果:将推理规则下半部分的语句实例加入KB
- 目标:要证明的语句状态
(这叫搜索证明,是模型枚举的一个替代方法)
7.5.2 归结原理
如果有两个子句 C 1 C_1 C1和 C 2 C_2 C2,其中 C 1 C_1 C1包含文字 l l l, C 2 C_2 C2包含互补文字 ¬ l \neg l ¬l,则可以通过合一操作生成一个新的子句 C C C,其中不包含 l l l和 ¬ l \neg l ¬l。
具体地,可以表示为:
C 1 ∨ l C 2 ∨ ¬ l C 1 ∨ C 2 \frac{C_1 \vee l \quad C_2 \vee \neg l}{C_1 \vee C_2} C1∨C2C1∨lC2∨¬l
这个公式表示了单元归结的规则:选择两个子句,一个包含文字 l l l,另一个包含互补文字 ¬ l \neg l ¬l,然后通过合一操作生成一个新的子句 C C C,其中不包含 l l l和 ¬ l \neg l ¬l
from sympy.logic.boolalg import Or, Not
from sympy.logic.inference import satisfiable
def PL_RESOLUTION(KB, query):
clauses = KB + [Not(query)] # 将查询语句的否定形式添加到知识库中
new = clauses.copy() # 初始化新的子句集合
while True:
for C1 in clauses:
for C2 in clauses:
if C1 != C2: # 确保两个子句不相同
resolvents = PL_RESOLVE(C1, C2) # 应用归结规则生成新的归结子句
if Or() in resolvents: # 如果生成了空子句,返回True表示蕴含关系成立
return True
new += resolvents # 将生成的归结子句添加到新的子句集合中
if new == clauses: # 如果没有生成新的子句,返回False表示蕴含关系不成立
return False
clauses += new # 将新的子句集合添加到原始子句集合中
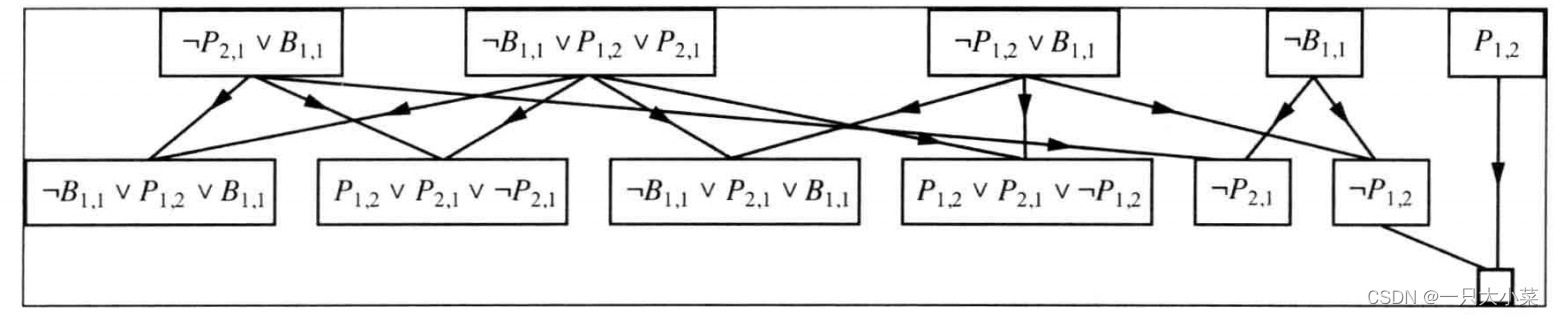
归结原理的完备性
归结闭包:给定子句集S,通过对S中子句或其派生子句反复应用归结规则而生成的所有子句的集合
完备性:如果子句集是不可满足的,那么这些子句的归结闭包包含空子句
7.5.3 horn子句和限定子句
限定子句:受限形式的一种子句,它是指恰好只含一个正文字的析取式。例如:(A∨B∨¬C)不是限定子句,而(A∨¬B∨¬C)是限定子句。
每个限定子句可写为蕴含式
Horn子句:至多只有一个正文字的析取式。如:(A∨¬B∨¬C)和(¬A∨¬B∨¬C)都是horn子句。
Horn子句在归结下是封闭的:如果对两个Horn子句进行归结,结果依然是Horn子句。
目标子句:没有正文字的析取式。如:(¬A∨¬B∨¬C)就是目标子句
7.5.4 前向链接和后向链接
前向链接
from collections import deque
def PL_FC_ENTAILS(KB, g):
count = {} # 记录子句前提中符号的数量
inferred = {} # 记录已推导过的符号
agenda = deque() # 存储已知为真的符号
# 初始化count和inferred
for clause in KB:
count[clause] = len(clause.PREMISE) # 初始化子句前提中符号的数量
inferred[clause] = False # 初始化已推导过的符号
for symbol in clause.PREMISE:
inferred[symbol] = False
# 将已知为真的符号添加到agenda
for symbol in KB.known_symbols():
agenda.append(symbol)
# PL-FC-ENTAILS算法主循环
while agenda:
p = agenda.popleft() # 从agenda中取出一个符号
if p == g: # 如果符号等于查询的命题符号,则返回True
return True
if not inferred[p]:
inferred[p] = True # 将符号标记为已推导过
for clause in KB:
if p in clause.PREMISE: # 如果符号在子句的前提中
count[clause] -= 1 # 减少子句前提中符号的数量
if count[clause] == 0: # 如果子句的前提中的所有符号都已推导过
agenda.append(clause.CONCLUSION) # 将子句的结论添加到agenda
return False # 循环结束时仍未找到查询的命题符号,返回False
后向链接
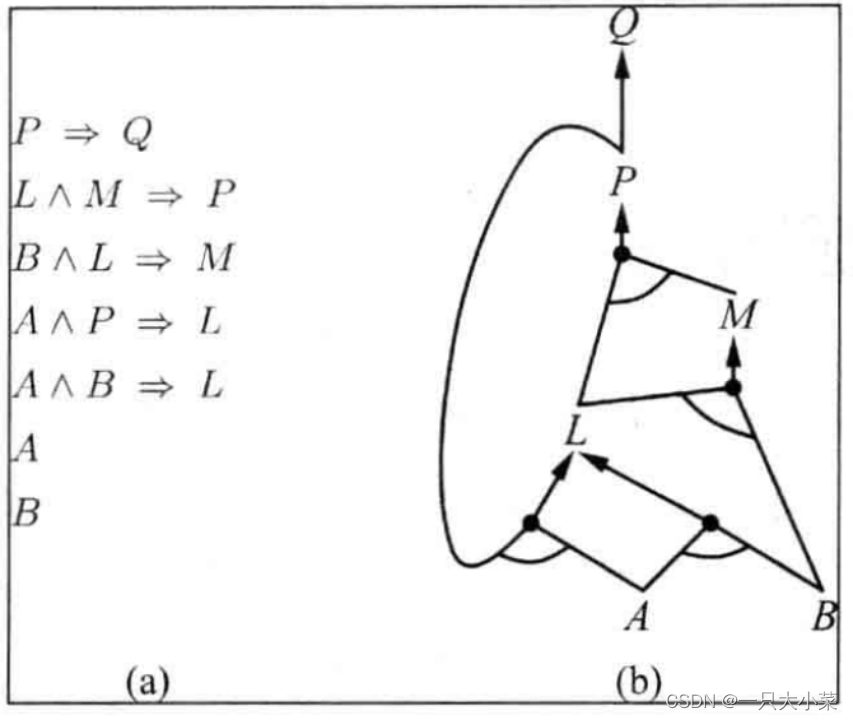
7.6 有效命题逻辑模型求解
可满足性问题第一个被证明是NP完全的问题,由于所有NP完全问题能在多项式时间内相互转化,因此高效可满足性判断算法理论上可用于任意NP的问题.
7.6.1完备的回溯算法
def DPLL_SATISFIABLE(s):
clauses = s.clauses() # 获取CNF表示中的子句集合
symbols = s.symbols() # 获取命题符号列表
model = {} # 初始化模型
return DPLL(clauses, symbols, model)
def DPLL(clauses, symbols, model):
if all_clause_true(clauses, model):
return True
if some_clause_false(clauses, model):
return False
P, value = find_pure_symbol(symbols, clauses, model)
if P is not None:
return DPLL(clauses, symbols - {P}, model.union({P: value}))
P, value = find_unit_clause(clauses, model)
if P is not None:
return DPLL(clauses, symbols - {P}, model.union({P: value}))
P = symbols[0]
rest = symbols[1:]
return DPLL(clauses, rest, model.union({P: True})) or DPLL(clauses, rest, model.union({P: False}))
7.6.2 不完备的回溯算法
特征:算法返回可满足的赋值说明公式可满足,否则不能区分公式是否可满足
代表算法:随机局部搜索,贪心法的变体,信念传播
代表性求解器:GSAT、WalkSAT、CCASat、BP、SP
def gsat(F, MAX_FLIPS, MAX_TRIES):
for i in range(MAX_TRIES):
o = randomly_generated_assignment(F) # 随机生成F的真值赋值
for j in range(MAX_FLIPS):
if satisfies(F, o): # 判断赋值o是否满足F
return o
v = variable_with_greatest_decrease(F, o) # 找到在赋值o下导致未满足子句数最大减少(可能为负)的变量
flip(v, o) # 翻转变量v在赋值o下的取值
return "FAIL"
7.7 基于命题逻辑的Agent
7.7.1 世界的当前状态
收集公理
如果方格中有微风,则其邻居方格中存在无底洞: Breeze(x, y) ⇔ (Pit(x+1, y) ∨ Pit(x-1, y) ∨ Pit(x, y+1) ∨ Pit(x, y-1)).
至少存在一个方格中有
Wumpus:Wumpus(1, 1) ∨ Wumpus(1, 2) ∨ … ∨ Wumpus(4, 4).
这些公理可以作为知识库的初始语句,用于基于命题逻辑的Agent进行推理和决策。需要根据Agent的感知信息动态更新知识库,以便Agent能够根据最新的信息进行推理和决策。
感知信息
- 时序变量:t
- 当前位置: L x , y t L^t_{x,y} Lx,yt
- 方向:
F
a
c
i
n
g
E
a
s
t
t
,
F
a
c
i
n
g
W
e
s
t
t
,
…
FacingEast^t , FacingWest^t, …
FacingEastt,FacingWestt,…
S t e n c h t , H a v e A r r o w t , W u m p u s A l i v e t Stench^t, HaveArrow^t, WumpusAlive^t Stencht,HaveArrowt,WumpusAlivet
感知信息: L x , y t = > ( S t e n c h t < = > S x , y ) L^t_{x,y} => (Stench^t <=> S_{x,y}) Lx,yt=>(Stencht<=>Sx,y)
Agent的感知信息动态更新知识库来描述现在的世界的状态。
效果公理
L 1 , 1 0 ∧ F a c i n g E a s t 0 ∧ F o r w a r d 0 ⇒ L 2 , 1 1 ∧ L 1 , 1 1 L^0_{1,1}∧ FacingEast^0∧ Forward^0 ⇒ L^1_{2,1} ∧L^1_{1,1} L1,10∧FacingEast0∧Forward0⇒L2,11∧L1,11
对于每个可能的时间步、16 个方格中的每一个方格、四个方向中的每一个方向,都需要一个这样的语句。对其他行动如:Grab、Shoot、Climb、TurnLeft 和 TurnRight,也同样需要类似的语句。
通过效果公式可以跟踪流的变化,将转移模型写成一组逻辑语句。
画面问题
效应公理并没有陈述行动的后果未改变哪些状态,引发了画面问题,有两种方式解决
一种是显示表示
F
o
r
w
a
r
d
t
=
>
(
H
a
v
e
A
r
r
o
w
t
<
=
>
H
a
v
e
A
r
r
o
w
t
+
1
)
Forward^t=>(HaveArrow ^ t<=>HaveArrow ^t+1)
Forwardt=>(HaveArrowt<=>HaveArrowt+1)
一种是后继状态表示
H
a
v
e
A
r
r
o
w
t
+
1
=
>
(
H
a
v
e
A
r
r
o
w
t
∧
¬
S
h
o
o
t
t
)
HaveArrow^{t+1}=>(HaveArrow^t ∧ \neg Shoot ^t)
HaveArrowt+1=>(HaveArrowt∧¬Shoott)