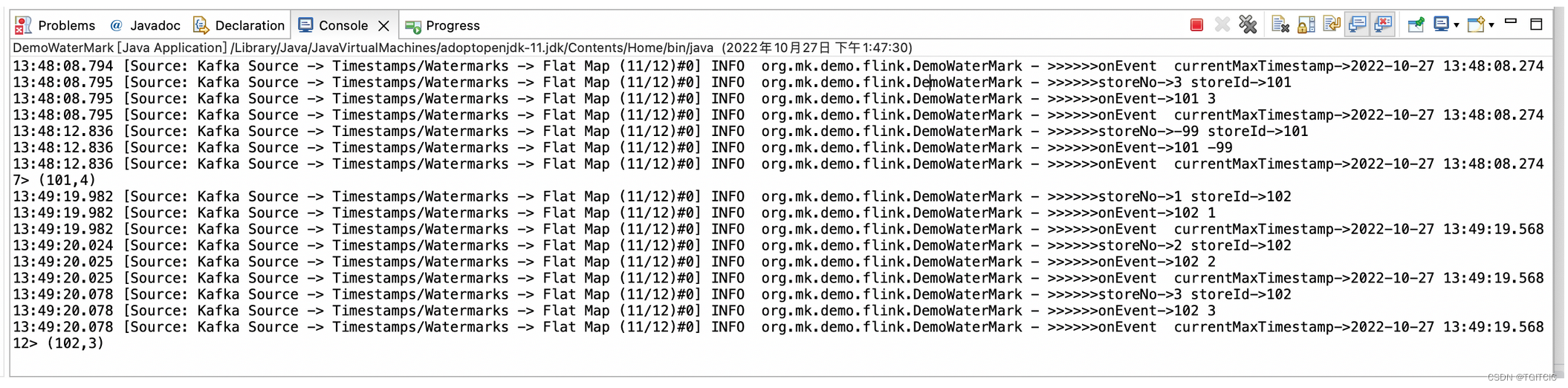
这章讲述模型框架和概念的时间较多，好像并没有涉及过多的运算，重在一些概念的理解。

Traditional Autoencoder

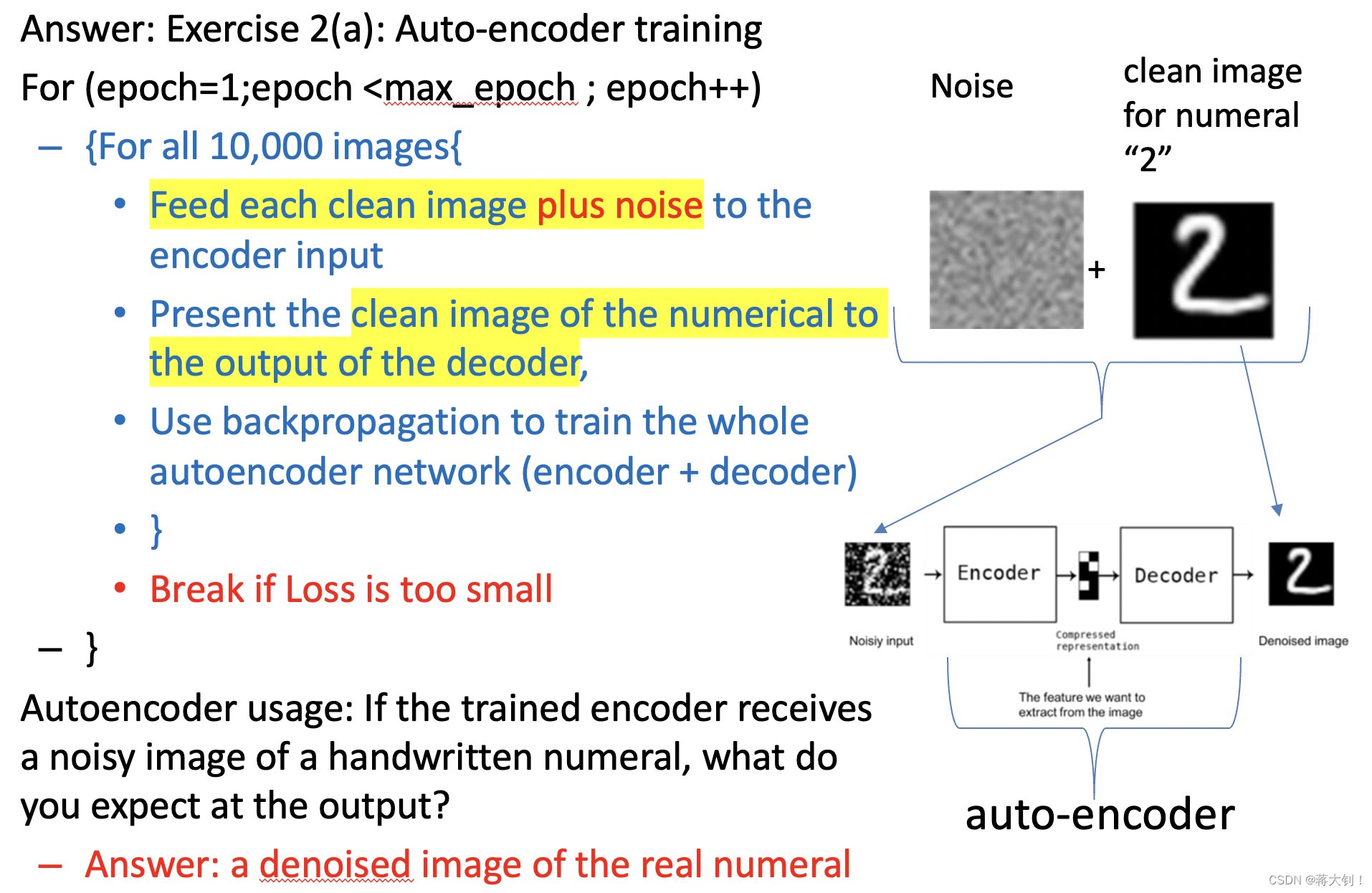
传统的自编码器常用来进行图像去噪的任务，需要了解其模型架构和流程。

自编码器由两部分组成：从Noisy Input到Z称为编码器，从Z到De-noised Output称为解码器。Input和Output有着相同的维度。

自编码器的最终目的是让X的重建误差最小，这样子能保证输入和输出尽可能地相似。

Auto-encoder的训练是一个无监督学习的过程，因为并不需要标记的数据训练。流程如下所示，它将纯净的图像+噪声整体放入encoder input，同时将纯净的图像放入decoder output，将forward processing得出的图像与纯净图像算出误差进行backpropagation训练。

Variational Autoencoder

Variational Autoencoder会从输入的图像中学习概率分布的参数，然后通过这些参数来产生新的图像。通过输入的图像X学到概率分布的变量$\mu$和$\sigma$，潜在参数$Z$的Sample从该概率分布中随机取样得到，接着放入Decoder进行重建。

其训练过程同Auto-encoder一致，在去噪任务中，将噪声图像放入input，纯净图像放入output，通过反向传播进行训练，其中的关键在于反向传播过程中损失Loss的定义，损失的定义中有两项。

先对相关参数进行定义，
$q_{\theta (en)}(z|x_i)$ 表示接受输入数据$x_i$，返回潜在变量$Z$（$Z$是由$\mu$和$\sigma$随机产生的），可以从$Z$中进行Sampling，$\theta (en)$代表encoder的weights和bias。

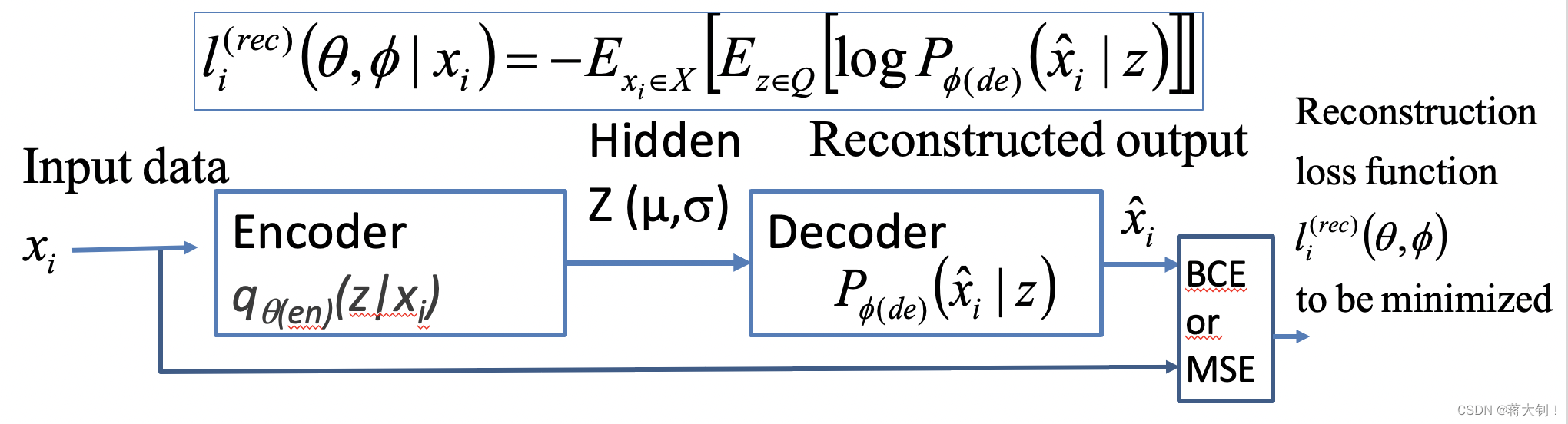
$P_{\varphi (de)}({\hat{x}}_i|z)$接受潜在变量$Z$产生的Sample，得到输出为$\hat{X}$，$\varphi (de)$代表decoder的weights和bias。

重建的损失$l_i(\theta ,\varphi )=-E_{x_i\in X}[E_{z\in Q}[log{P}_{\varphi (de)}({\hat{x}}_i|z)]]$需要尽可能地小。由于$P$为高斯分布，因此可以对上式重写为=$\frac{1}{N}\sum _{x_i\in X}(\frac{1}{2{\sigma }_{\widehat{x_i}|z}^2}(x_i-{\mu }_{\widehat{x_i}|z}{)}^2)$.

Kullback–Leibler divergence

但是会存在的问题是，同样$l_i(\theta ,\varphi )$较小，$q_{\theta (en)}(z|x_i)$和$P_{\varphi (de)}({\hat{x}}_i|z)$的差异很大，显然不是来自相同的分布。因此这里引入了Kullback–Leibler divergence 来衡量两个分布的差异程度，$D_{KL}[q_{\theta (en)(z|x_i)}||(N(0,I)]$衡量了差生图像分布与标准高斯分布的差异。

最终该模型的Loss定义为$L^{(all)}=\frac{1}{N}\sum _{x_i\in X}(\frac{1}{2{\sigma }_{\widehat{x_i}|z}^2}(x_i-{\mu }_{\widehat{x_i}|z}{)}^2)+D_{KL}[q_{\theta (en)(z|x_i)}||(N(0,I)]$，其物理意义为在局部的概率分布中，产生与输入误差最小的输出。

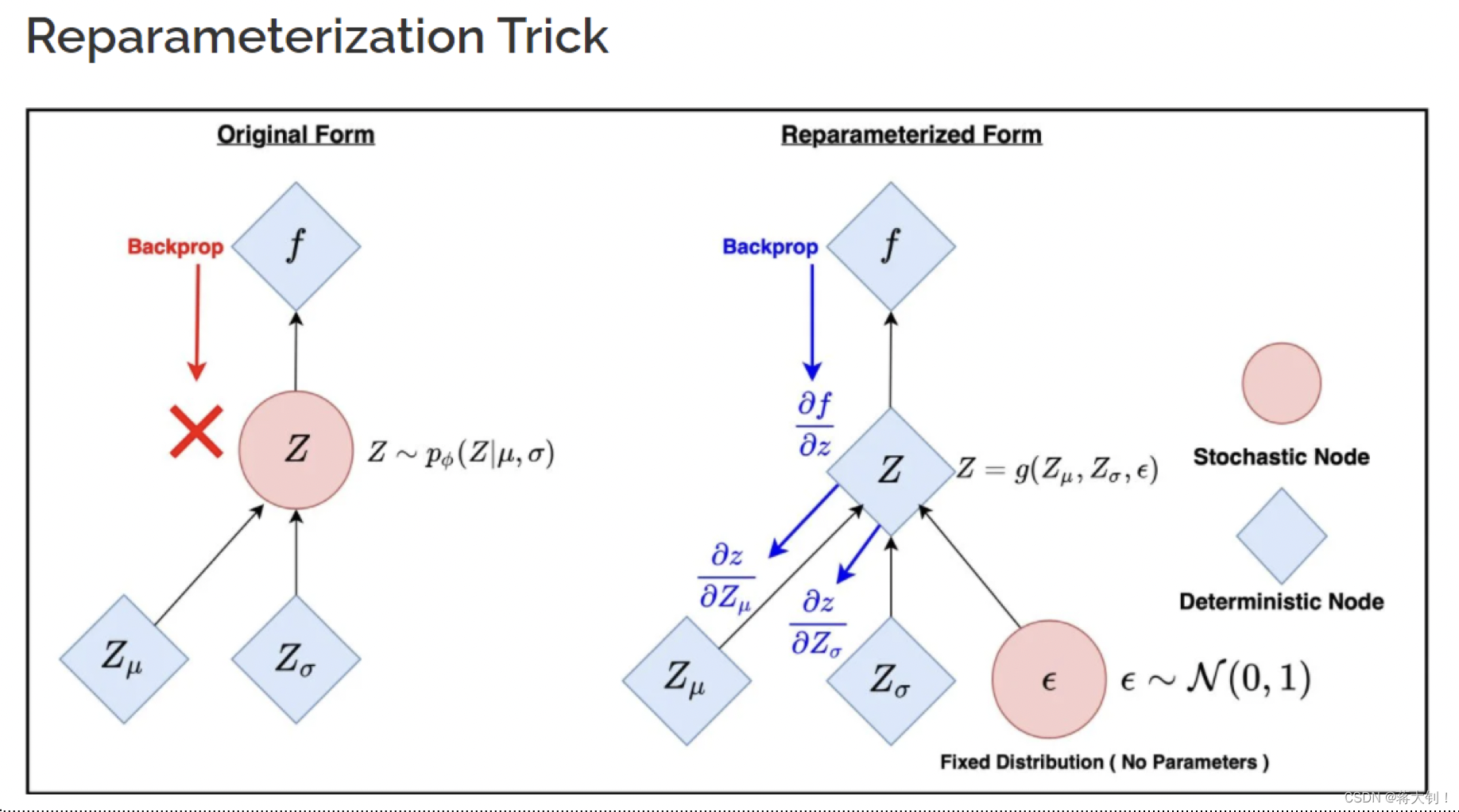
Reparameterization

在模型构建的过程中，潜在变量$Z$在$\mu$和$\sigma$固定的情况下涉及了random选择sample的过程，不能通过backpropagate进行训练，因此引入了reparameterization trick. 其将原先平均值为$\mu$，标准差为$\sigma$的高斯分布，表示为$Z=ϵ\cdot {\sigma }_x+{\mu }_x$，其中$ϵ\in N(0,1)$，这样子任意的$Z$都可以通过对$N(0,1)$的缩放表示出来。

该方法让原先随机化的过程确定化，从而能够进行backpropagation.