-
数据是对客观事物的符号表示
-
元素之间的关系不同,通常由四类基本结构————集合,线性结构,树形结构,图状结构
-
算法的五个特性——出入确可穷
1个或多个输出 0个或多个输入 确定性 可行性 有穷性 -
求下列程序段的时间复杂度
for(i=1;i<=n;i++) for(j=1;j<=n;j++) { C[i][j]=0; for(k=1;k<=n;k++) C[i][j]+=a[i][k]*B[k][j] }
我的理解:外圈有效循环n次,中圈执行n次,内圈执行n次,就是O(n^3)
-
再长度为n的顺序表的第i个元素a之前插入一个元素,需要移动n/2个元素
-
入栈顺序位abcdefg,出栈第一个元素是g,则出栈第五个元素是?
我的理解: g第一个出来,那abcdef也就都进去了, 所以第五个出来的只能是c -
深度为10的满二叉树,有几个节点
(2^10)-1 -
二叉树中有100个度为2的节点,则该二叉树有几个叶子节点
性质3,叶子节点=度为2的节点数+1=101 -
无向图有20个顶点,当有多少条边时,称为完全无向图
我的理解:完全无向图:该图中每条边都没有方向,任意两个顶点间都存在边 ,三个顶点,第一个顶点射出两条边,第二个顶点射出一条边,所以20个顶点就是1+2+3+4+5+…+19=190
-
不稳定的排序:快希选堆
-
稳定的排序:冒泡,插入,排序
-
循环队列的最大长度为6,队列中已有3个元素,对头元素是a,队尾元素是c,依次进行三个步骤,d入队,e入队,一个元素出队。求front,rear下标
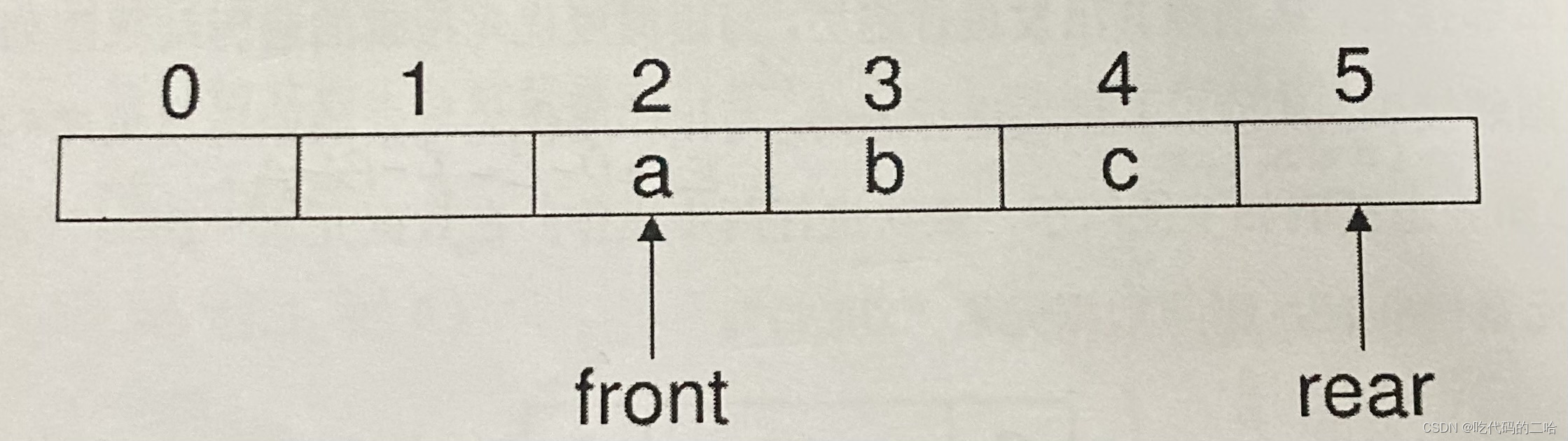
我的理解:循环队列,入队是rear+1,出队是front+1
d入队,e入队,队列的r+2到1了,一个元素出队f+1到3 -
二叉树的后序遍历为DCBFJIHGEA,中序为BCDAFEHJIG,画出二叉树求先序
我的理解:根据后序遍历得到A为根,看A在中序哪里,是不是在中间,就说明,根的左边有BCD,根的右边有FEHJIG。再看后序遍历的,后序遍历的是从右向左看噢,所以看完了根,再看E,中序里E再A的左边,也就是说E是A的右孩子,记住先看根节点是谁,怎么看根节点是谁呢,先序的第一个元素就是根节点,因为先序遍历时是根左右嘛,后序遍历的最后一个节点是根节点,因为后序遍历的是左右根。找到根节点是谁之后,根据中序遍历看看其他节点大致的分布在根节点的两边,再根据先序从左往右,后序从右往左的一个一个找元素,找到一个元素拿到中序里看他在父节点的哪边。再写出他的先序遍历,先序是根左右,ABCDEFGHIJ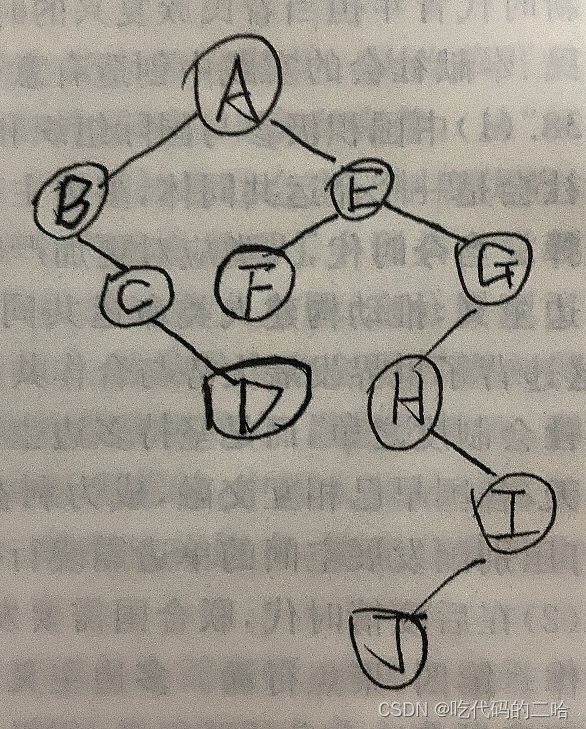
-
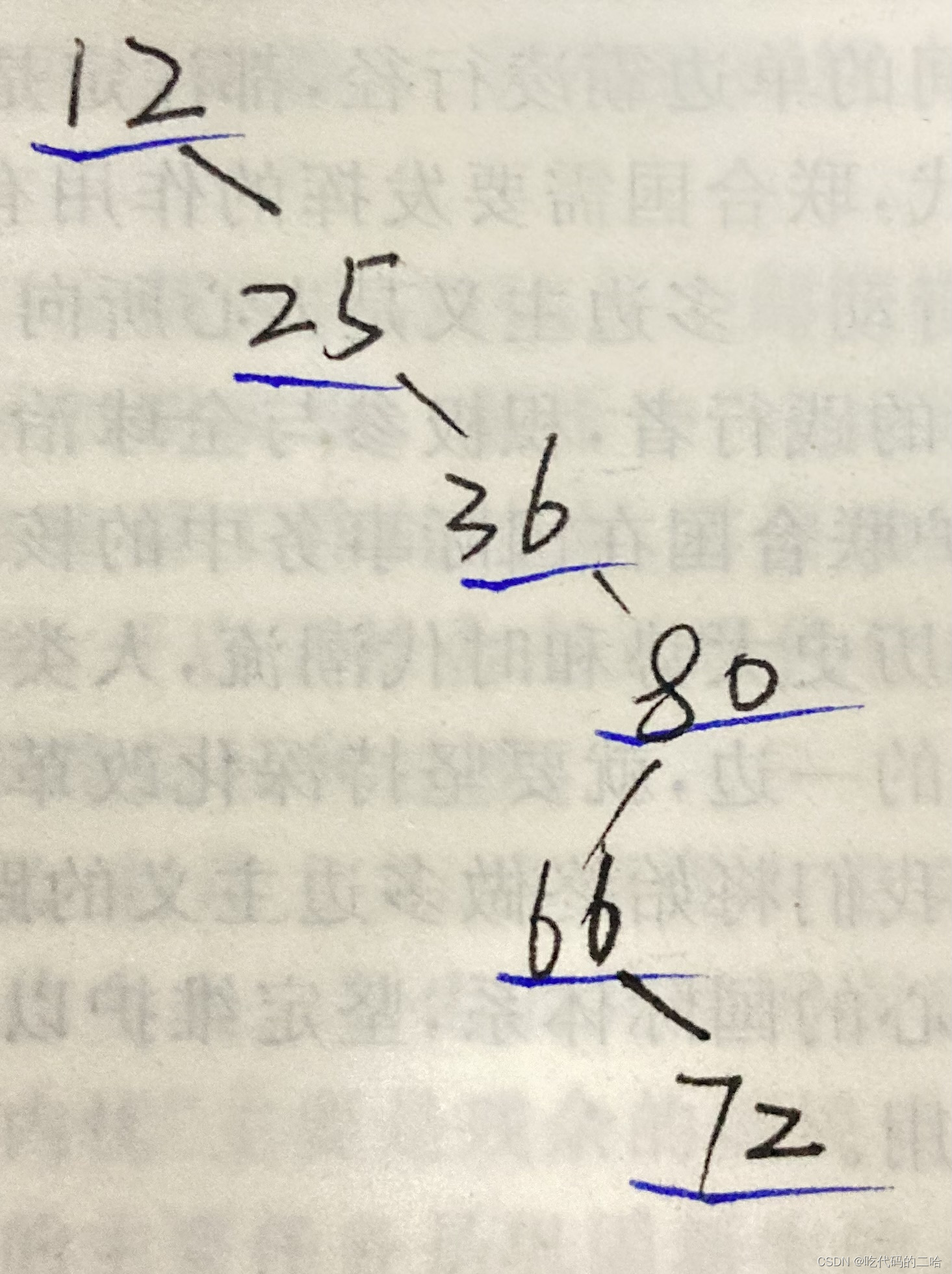
关键字序列为12,25,36,80,66,72构造二叉排序树,求平均查找长度
我的理解:第一个关键字为根,大于他的为右孩子,小于它的为左孩子,画出来就行了,平均查找长度,关键字分布的层数相乘 (1+2+3+4+5+6)/6=21/6=3.5
-
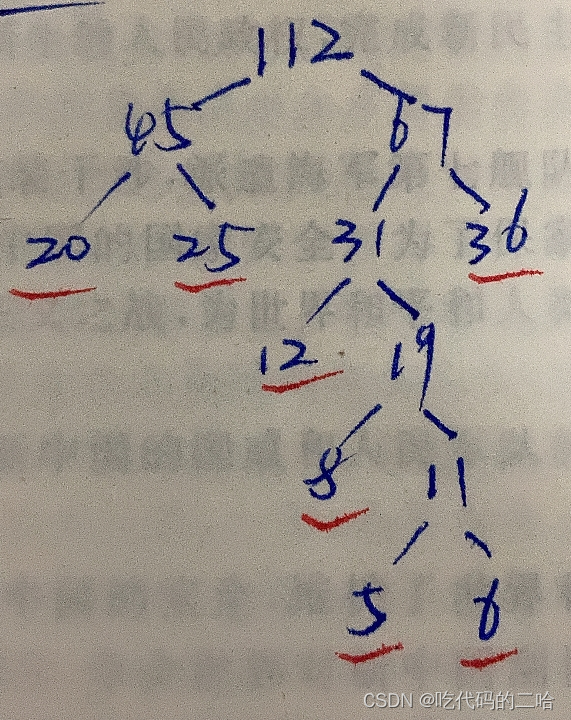
12,8,6,20,36,25,5画出哈夫曼树,求带权路径长度
我的理解:每次选最小的两个数相加加完后,整理一下树,再看每个叶子节点的权长,最后相加,权就是边嘛,全部相加就是[(20+25+36)x2+12x3+8x4+(5+6)x5]/7=285/7
16.无向图的邻接表
E到1,2,3,4,5然后为空,1,2,3,4,5分别表示ABCDF,这么画就ok了
求A的度,就是看A有几条边呗,A的度为2,以B出发求深度优先,B-A-E-F-C-D,深度优先就是一条路走到低,到低了再返回上一步,举个例子,B先到的A,再就从A开始走,A走到E,E可以随便走一个没有走过的,比如E-F,F再走C,C下一步没有未被访问的点了,就回退到F,再退到E,E发现D没被访问,于是就去访问D。书顺序就是B-A-E-F-C-D。广度优先呢,举个例子,E的广度优先搜索就是E-A-B-F-C-D也可以是E-D-C-F-B-A还几种都可以的,那B的广度优先搜索遍历呢B-A-E,B到了A,E,E可以到-F-C-D。所以结果可以是B-A-E-F-C-D -
直接插入排序
我的理解:直接插入排序是从第二个数开始,依次和前面的数比较,前面的数如果大于它,前面的数就后移,这就是大概思路int sort(int A[],int length) { int i,j,temp; for(i=1;i<length;i++) #这里的i表示下标 { temp=A[i]; for(j=i-1;j>=0&&A[j]>A[I];j--) { A[j+1]=A[j]; #前面存在一个大于A[i]的数就把大于A[i]的数后移 #不用担心是否存在这样一种情况 9,2,3 #A[i]为3,2小于3,则不动,j--,A[j]=9,9>3就要后移 #注意哈,不存在以上这种情况,9,2早就被循环给调正了, } A[j+1]=temp; #假如是1,2,3这种情况 #A[i]=2,A[j]=1,1不小于2,所以j不--,跳出循环,再执行A[j+1]=temp,还是把2赋值给了2,也没有影响噢。 } } -
简单选择排序
我的理解:从第一个数开始,与自己和其他数比较,存在一个小于自己的数时,记住他的下标,再从该下标往后找一个小于该下标的数,记住新的小数的下标,直到找到结尾,找到结尾以后,就找到了最小的数的下标,利用temp与一个数交换位置,最小的数就去了头。再从第二个数开始,与自己和其他数比较,一旦找到一个小于自己的数,就记住他的下标,从该下标往后找一个更小的数,又记住更小的数的下标直到找到尾巴。再利用temp把最小的数放在第二个位置。再从第3个数开始…int select(int A[],int length) { int i,j,temp,min; for(i=0;j<length;i++) { min=i; for(j=i;j<=length&&A[j]<A[min];j++) { min=j; } temp=A[i]; A[i]=A[min]; A[min]=temp; } } -
输出1000以内的质数
我的理解:用一个for循环去让n除2到n-1,等于==0就不是int prime(int n) #传入一个n进来 { int j; for(j=2;j<n;i++) if(n%j==0) return 0; return 1; } int main() { int i,a=0; for(i=2;i<1001;i++) { if(prime(i)) { printf(“%d”,i); a++; if(a%10==0&&a!=0) printf(“/n”); } } }
我的理解:传入一个n到prime,就需要j从2开始到n-1,n一个一个除,需要从2除到n-1都不为0,则n为质数,当n为质数时prime返回1,if真,执行:打印i,且a++,a加到10或者20,30之类的,就打印一个换行符,