一、问题与数据

研究者想调查人们对“本国税收过高”的赞同程度：Strongly Disagree——非常不同意，用“0”表示；Disagree——不同意，用“1”表示；Agree--同意，用“2”表示；Strongly Agree--非常同意，用“3”表示。

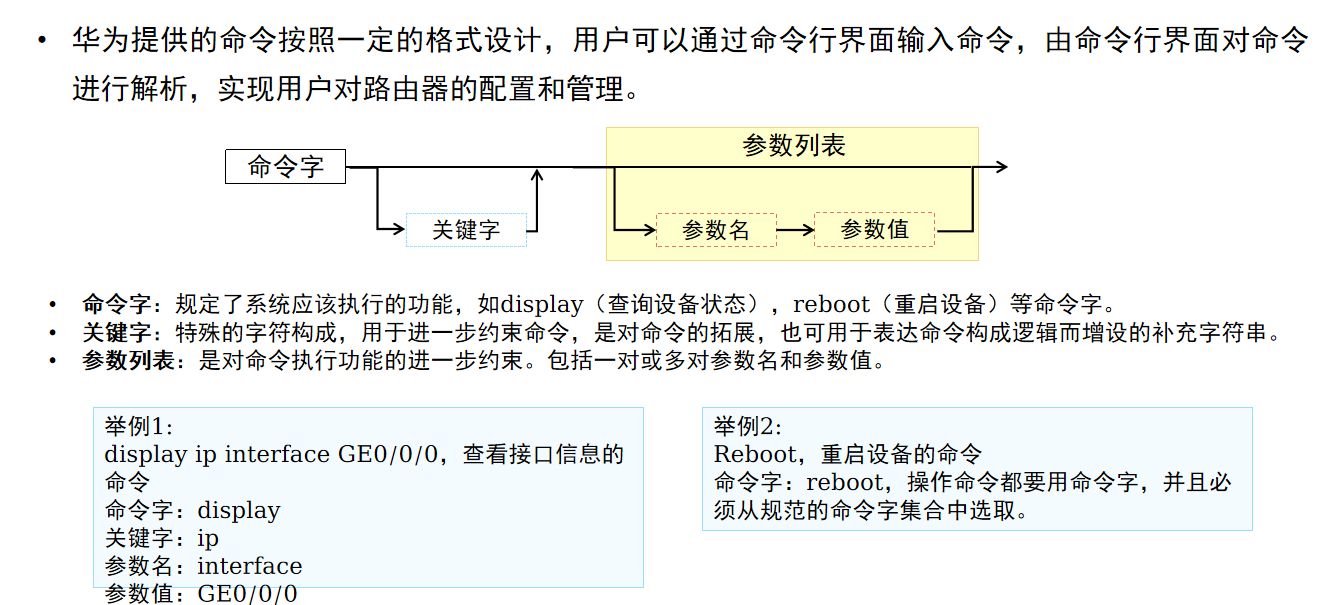
另外，研究者也调查了一些其它情况，包括：是否是“雇主”（biz_owner：Yes——是，用“0”表示；No——否，用“1”表示）、年龄（age）和党派（politics：Lib——党派1，用“1”表示；Con——党派2，用“2”表示；Lab——党派3，用“3”表示）。部分数据如下图：

二、对问题的分析

使用有序Logistic进行回归分析时，需要考虑4个假设。

• 假设1：因变量唯一，且为有序多分类变量，如城市综合竞争力等级可以分为高、中、低；某病的治疗效果分为痊愈、有效、无效等。
• 假设2：存在一个或多个自变量，可为连续、有序多分类或无序分类变量。
• 假设3：自变量之间无多重共线性。
• 假设4：模型满足“比例优势”假设。意思是无论因变量的分割点在什么位置，模型中各个自变量对因变量的影响不变，也就是自变量对因变量的回归系数与分割点无关。

有序多分类的Logistic回归原理是将因变量的多个分类依次分割为多个二元的Logistic回归，例如本例中因变量“本国的税收过高”的赞同程度有4个等级，分析时拆分为三个二元Logistic回归，分别为(0 vs 1+2+3) 、(0+1 vs 2+3)、(0+1+2 vs 3)，均是较低级与较高级对比。

在有序多分类Logistic回归中，假设几个二元Logistic回归中，自变量的系数相等，仅常数项不等，结果也只输出一组自变量的系数。因此，有序多分类的Logistic回归模型，必须对自变量系数相等的假设（即“比例优势”假设）进行检验（又称平行线检验）。如果不满足该假设，则考虑使用无序多分类Logistic回归。

三、前期数据处理

对假设进行验证前，我们需要将分类变量设置成哑变量。

1. 为什么要设计哑变量

若直接将分类变量纳入Logistic回归方程，则软件会将分类变量按连续变量处理。例如，如果把性别按“1”——男、“2”——女进行编码，然后直接把性别纳入方程，方程会认为“女”是“男”的2倍。为了解决这个问题，需要用一系列的二分类变量“是”或“否”来表示原始的分类变量，这些新的二分类变量被称为“哑变量”。

在SPSS软件的二项Logistic回归模型中，将分类变量选入categorical，软件会自动设置一系列的哑变量。由于验证假设3(自变量之间无多重共线性)需要通过线性回归实现，而在线性回归中，就需要手动设置哑变量。因此，这里需要先手动设置哑变量。

2. 设置哑变量的思路

哑变量的数目是分类变量类别数减一。本例中，党派1、党派2和党派3的原始编码为1、2和3。设置哑变量时，需要对党派1和党派2进行重新编码。

建立新变量Lib（党派1），若调查对象选了党派1，则Lib编为“1”，代表是；若未选党派1，则Lib编为“0”，代表否。同样，建立新变量Con（党派2），将是否选党派2编为“1”或“0”。此时，若既未选党派1，又未选党派2，则两个新变量Lib和Con的编码都为“0”，代表党派3。此时，党派3在模型中是参考类别（Reference）。

3. 在SPSS中设置哑变量

(1) 首先，先创建新变量“Con”，在主菜单下选择Transform→Recode into Different Variables... ，如下图：

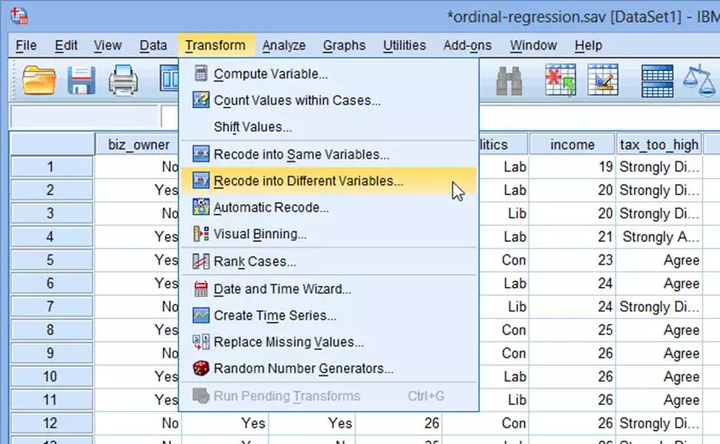
(2) 在Recode into Different Variables对话框中，将politics选入右侧Numeric Variable-->Output Variable下，在右侧Output Variable中填写“Con”。点击Change→Old and New Values。

(3) 出现Recode into Different Variables: Old and New Values对话框，在左侧的Old Value下的Value中填入2，在右侧的New Value下的Value中填入1，点击Add。

(4) 将其它值变为“0”：左侧点击All other values，在右侧Value中填入“0”，点击Add→Continue。

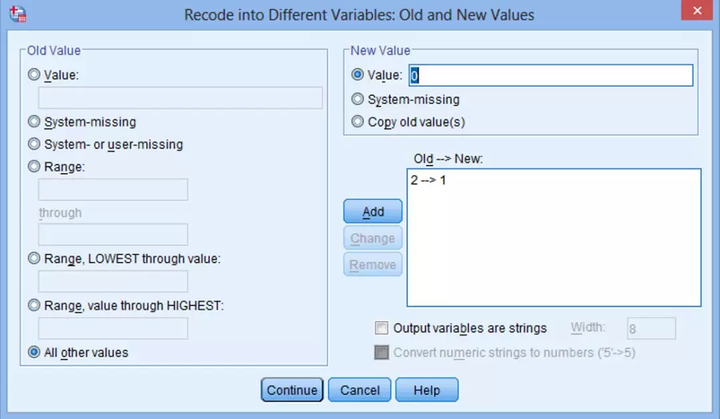
(5) 如果数据中有缺失值，点击左侧System-missing，右侧点击System-missing→Add，保持缺失值：

设置得到的结果如下图：

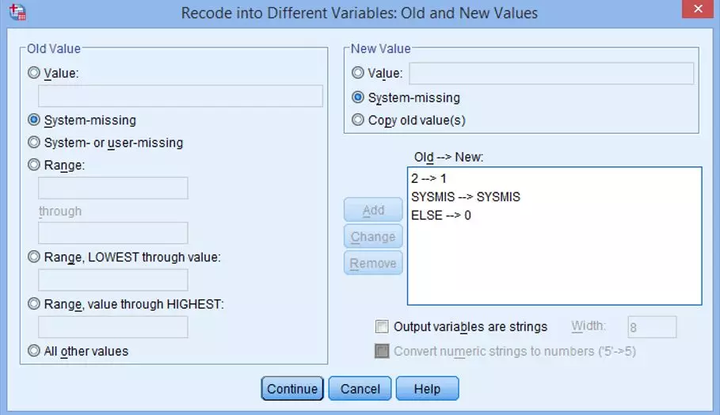
本例中没有缺失值，可省略这一步。

(6) 继续创建新变量“Lib”，与以上步骤相似。两个变量创建完成后，点击变量视图，可以看到在最右侧已经生成了两个新变量“Con”和“Lib”，如下图：

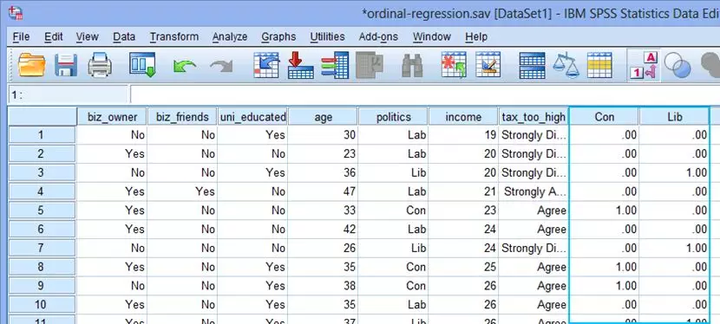
四、对假设的判断

假设1-2都是对研究设计的假设，需要研究者根据研究设计进行判断，所以这里主要对数据的假设3-4进行检验。

1. 检验假设3：自变量之间无多重共线性

(1) 在主菜单点击Analyze→Regression→Linear...

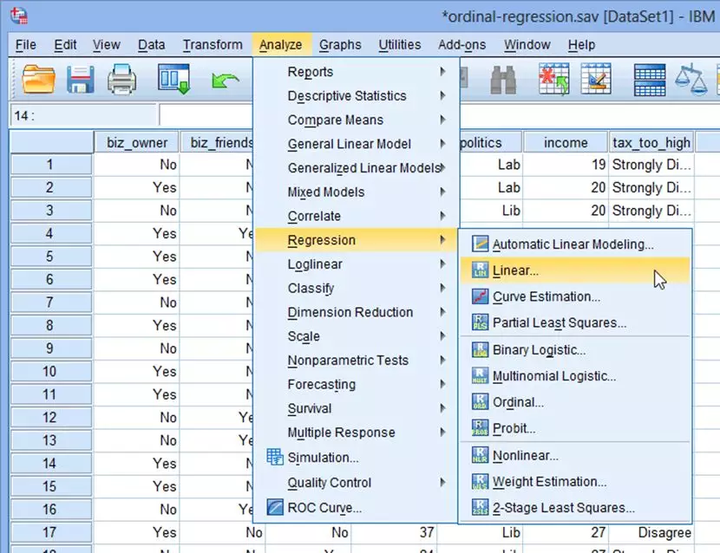
(2) 将tax_too_high选入Dependent，将biz_owner、age、Con、Lib选入Independent(s)。

(3) 点击Statistics，出现Linear Regression：Statistics对话框，点击Collinearity diagnostics→Continue→OK。

结果如下图：

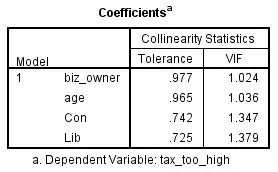
如果容忍度（Tolerance）小于0.1或方差膨胀因子（VIF）大于10，则表示有共线性存在。

本例中，容忍度均远大于0.1，方差膨胀因子均小于10，所以不存在多重共线性。如果数据存在多重共线性，则需要用复杂的方法进行处理，其中最简单的方法是剔除引起共线性的因素之一，剔除哪一个因素可以基于理论依据。

2. 检验假设4：模型满足“比例优势”假设

“比例优势”假设可以在后面结果部分的“平行线检验”中看到。

五、SPSS操作

SPSS中，可以通过两个过程实现有序Logistic回归。分别是Analyze → Regression → Ordinal...和Analyze → Generalized Linear Models → Generalized Linear Models...。

其中，Analyze → Regression → Ordinal模块，可以检验 “比例优势”假设，但无法给出OR值和95%CI。而Analyze → Generalized Linear Models → Generalized Linear Models模块可以给出OR值和95%CI，但无法检验“比例优势”假设。

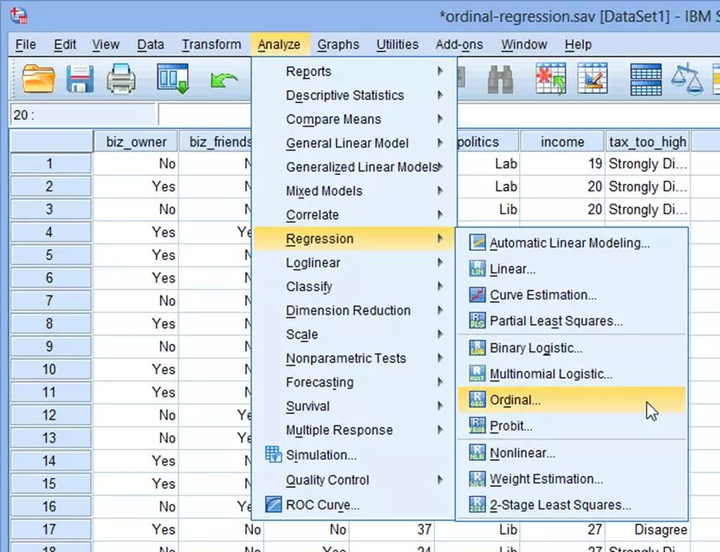
这里，我们主要介绍Analyze → Regression → Ordinal过程。

(1) 在主菜单点击Analyze→Regression→Ordinal...