1. 图的基本概念

教程：图的基本结构
图是一种相较于链表和树更为复杂的数据结构。在线性表中，数据元素之间仅有线性关系，每个元素只有一个直接前驱和一个直接后继（每个元素之间一个一个逐个相连）。在树形结构中，数据元素之间有着明显的层次关系，上一层元素能和下层多个元素相关，但是下层元素只能与一个上层元素相关。而在图结构中，节点之间的关系任意，任何两个顶点都可能相连。
图结构如图所示

二、图的术语
接下来介绍图结构中的一些术语。
1.顶点 ：图中的数据元素通常称为顶点。
2.边 ：两顶点间的连线称为边。
3.V是顶点的有穷非空集合。
4.VR是两个顶点之间关系的集合，也是边的集合。
5.通常表示为:G(V,E),G表示一个图，V是图G中顶点的集合，E是图G中边的集合。
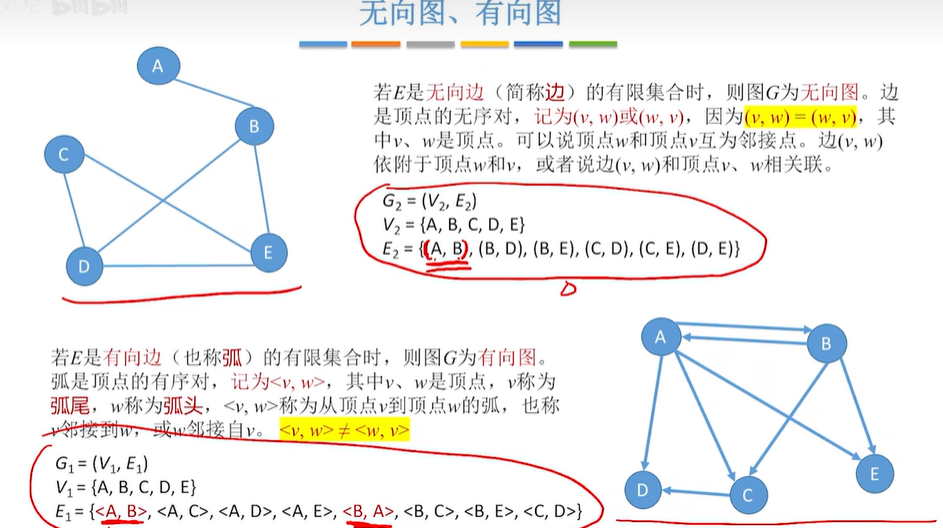
6.无向边：若顶点A到顶点B的边没有方向，称这条边为无向边，用无序偶对(A,B)或(B,A)表示。

7.有向边：若顶点A到顶点B的边有方向，称这条边为有向边，也称为弧(Arc)，用有序对 < B, A >表示；B表示弧尾，A表示弧头
8.由无向边构成的图为无向图
9.由有向边构成的图为有向图

G：Graph
V：Vertex
E： Edge

1.1 图逻辑结构的应用

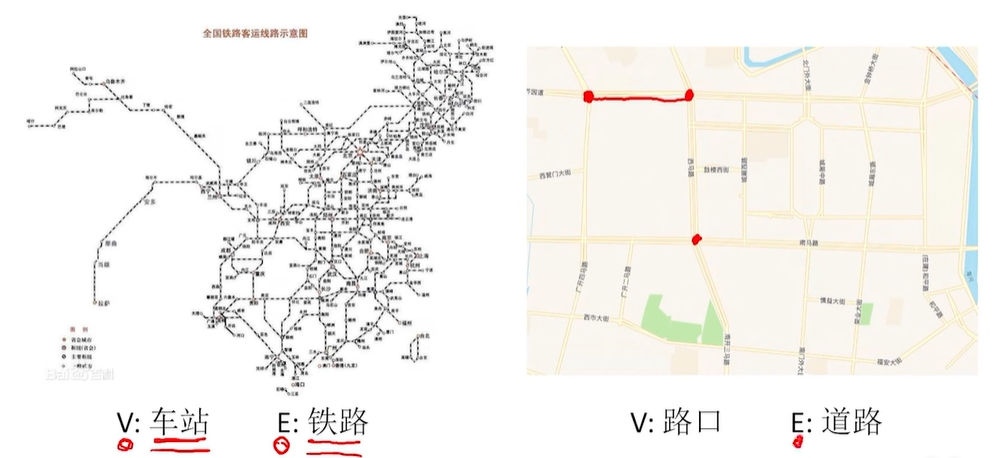
1.2 无向图，有向图

1.3 简单图，多重图

1.4 顶点的度，入度和出度

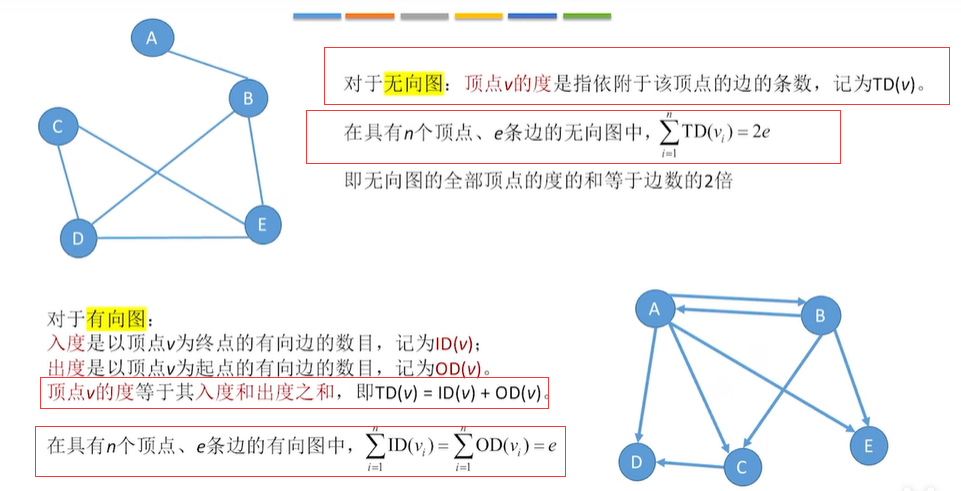
1.5 顶点和顶点的关系描述

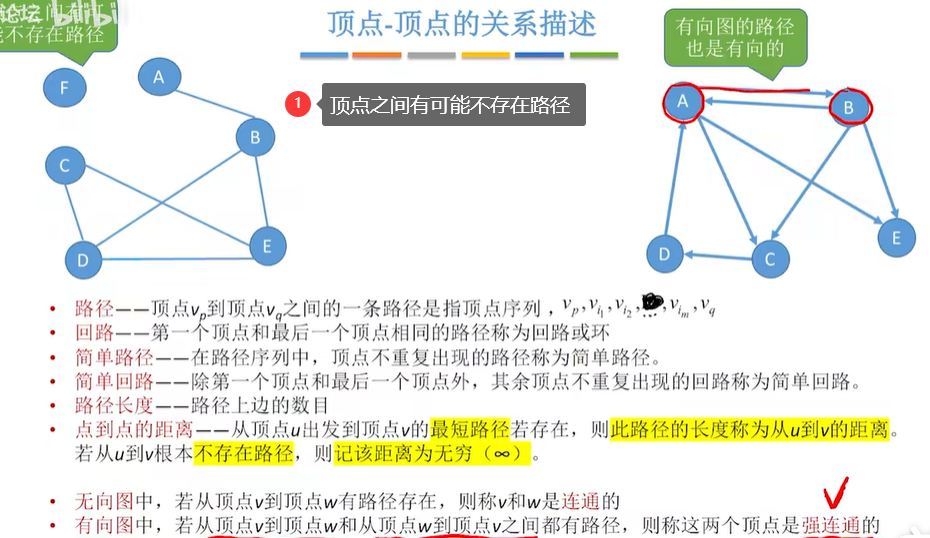
1.6 连通图，强连通图

• 连通图是无向图
• 强连通图是有向图
  
  

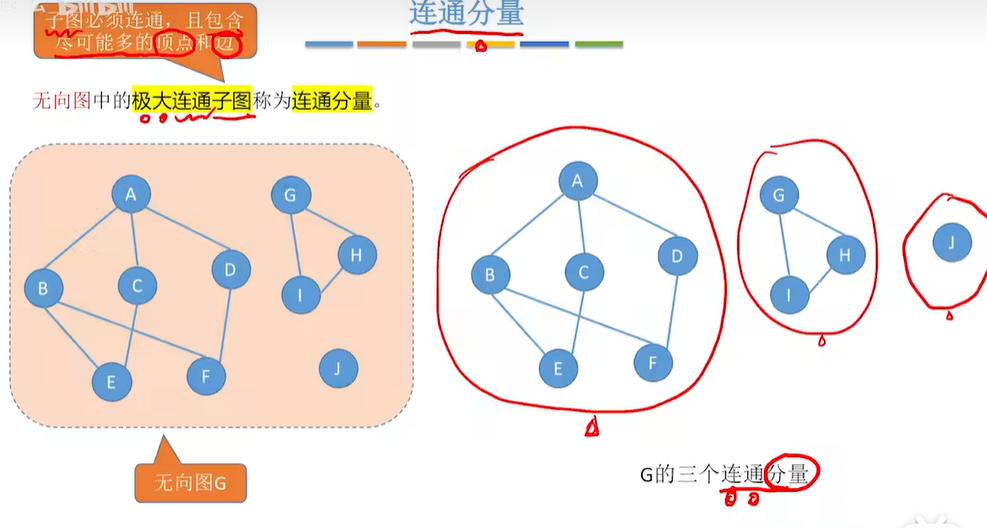
1.7 研究图的局部——子图

1.8 生成树

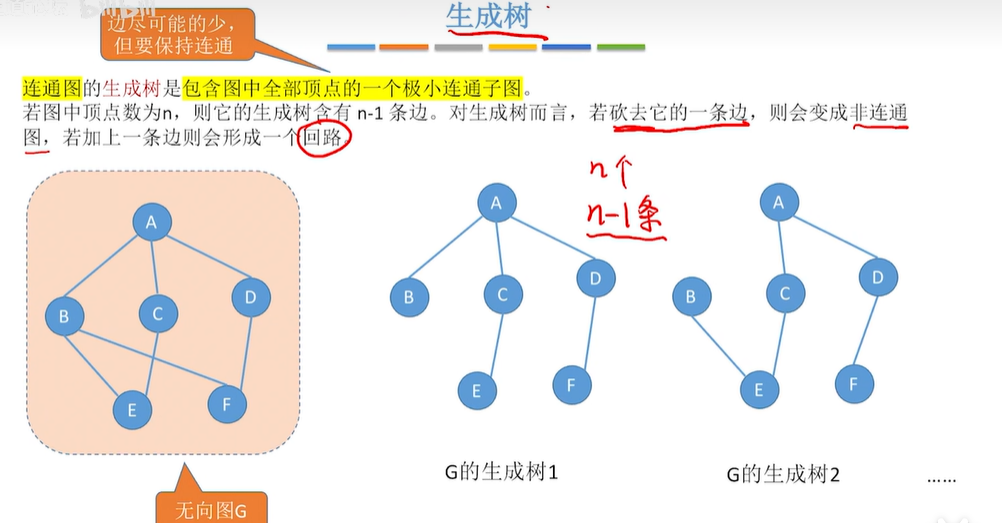
1.9 生成森林

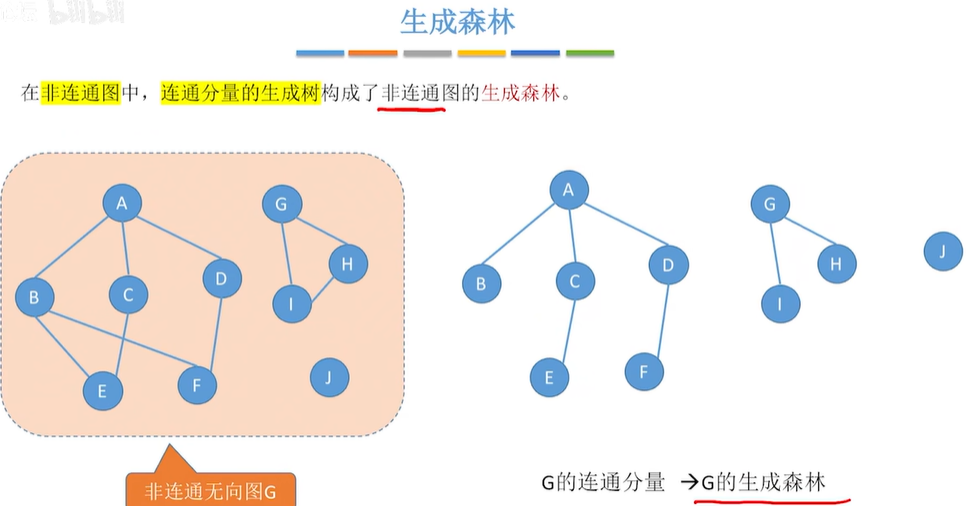
1.10 边的权，带权图/网

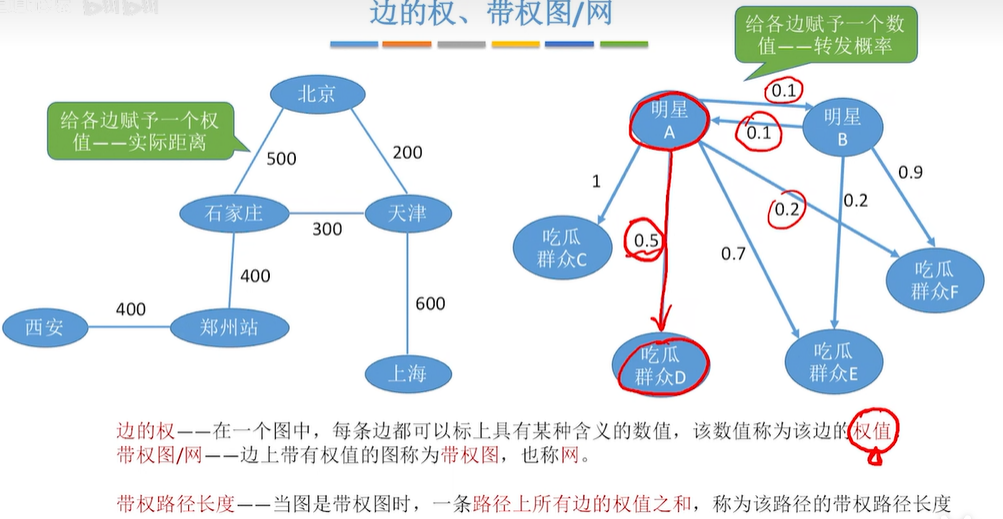
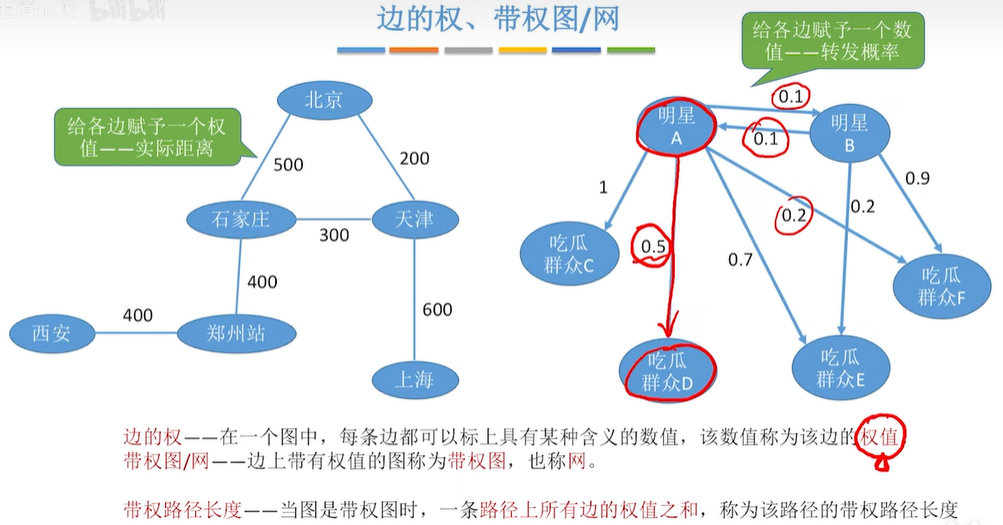
1.11 无向完全图，有向完全图

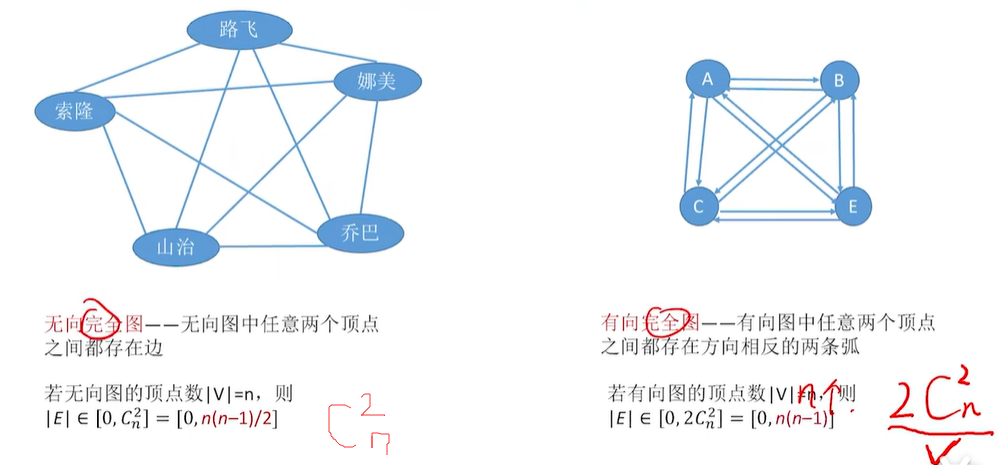
1.13 树、有向树

2. 图的存储及基本操作

教程：图的存储及基本操作

2.1 邻接矩阵法

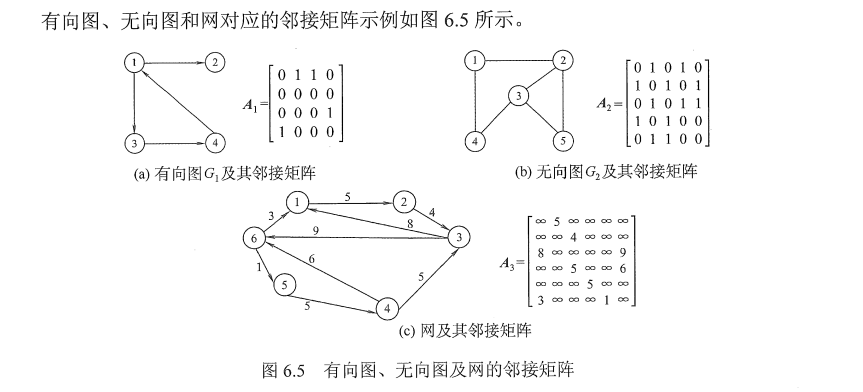
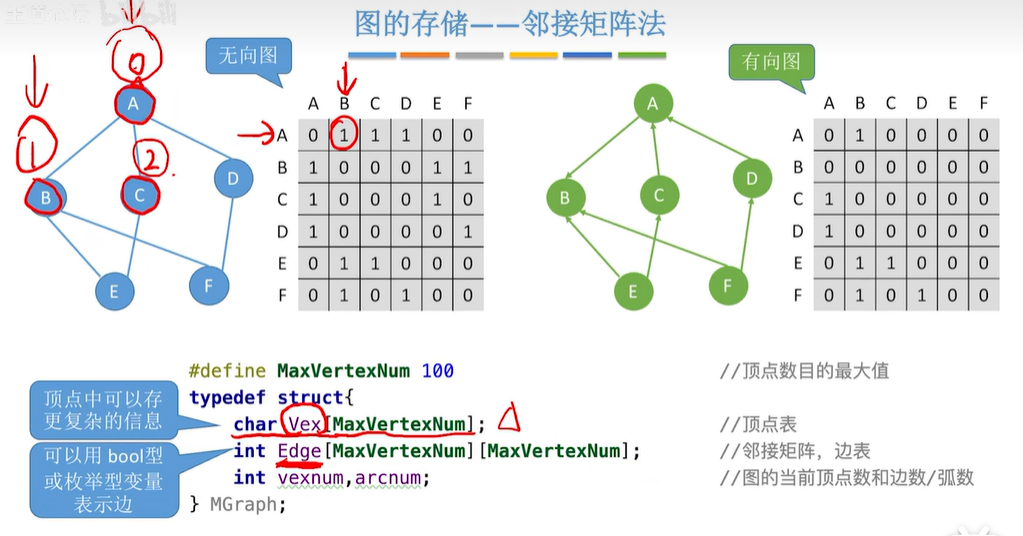
图的邻接矩阵存储结构定义如下:

#define MaxVertexNum 100 // 顶点数目的最大值
typedef struct {
	char Vex[MaxVertexNum];//顶点表
	int Edge[MaxVertexNum][MaxVertexNum];//邻接矩阵，边表
	int vexnum,arcnum;//图的当前顶点数和边数/弧数
}MGraph;

2.1.1 如何求顶点的度、入度、出度？

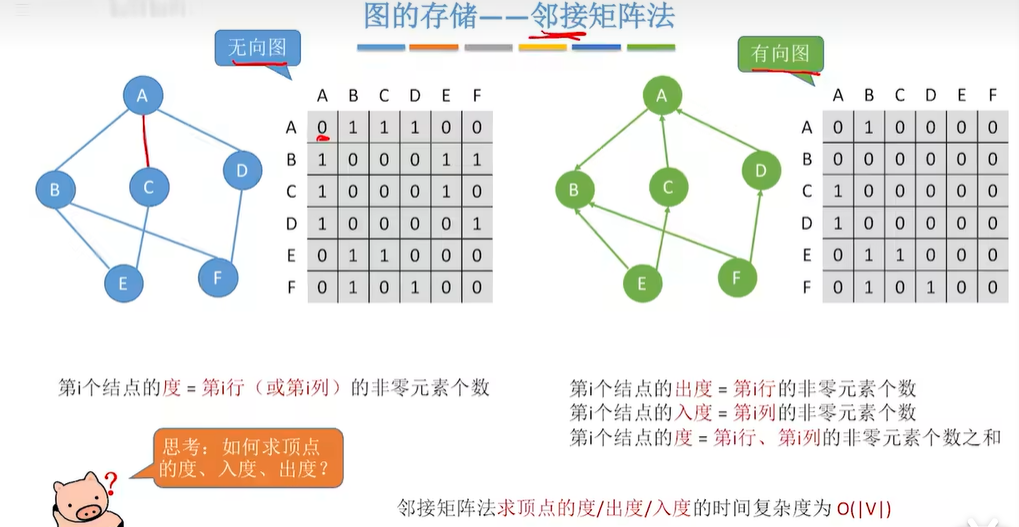
2.1.2 邻接矩阵法存储带权图（网）

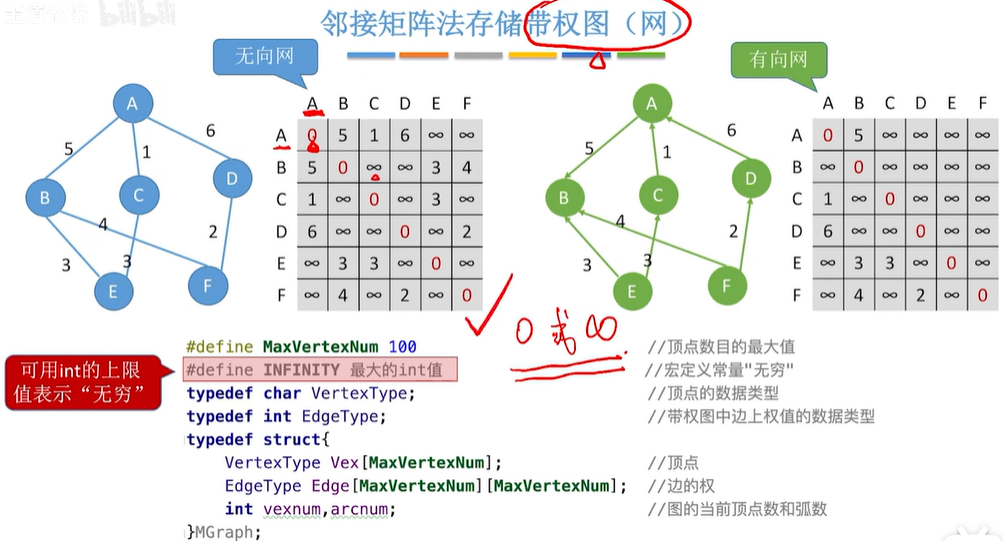
#define MaxVertexNum 100 // 顶点数目的最大值
#define INFINITY 最大值的int值// 宏定义常量“无穷”
typedef char VertexType;//顶点的数据类型
typedef int EdgeType; //带权图中边上权值的数据类型
typedef struct {
	VertexType  Vex[MaxVertexNum];//顶点表
	EdgeType Edge[MaxVertexNum][MaxVertexNum];//边的权
	int vexnum,arcnum;//图的当前顶点数和边数/弧数
}MGraph;

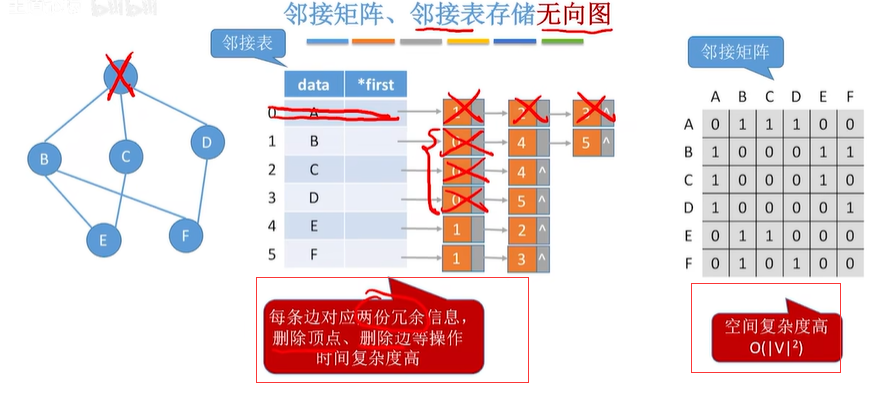
2.1.3 邻接矩阵法的性能分析

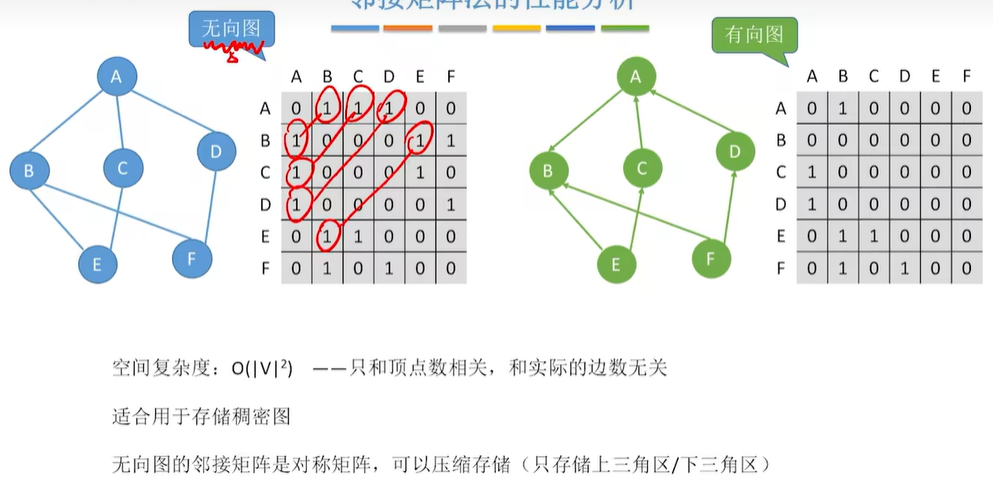
2.2 邻接表法

邻接表法

图的邻接表是一种顺序与链式存储相结合的存储方式。下面给出一个示例，以便大家能够理解邻接表这种存储方式：
无向图G1

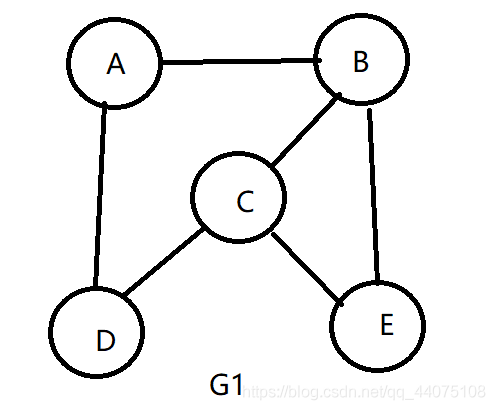
用邻接表来存储G1

每一个顶点所在结点都是之后链表的头结点，之后的链表结点存放从头结点所存顶点能够直接到达顶点的位置下标，如顶点A能够直接到达D，B两个顶点，D的顶点存放在3位置，B顶点存放在1位置，所以A之后的链表结点存放的值为3和1

二、结构
结构图



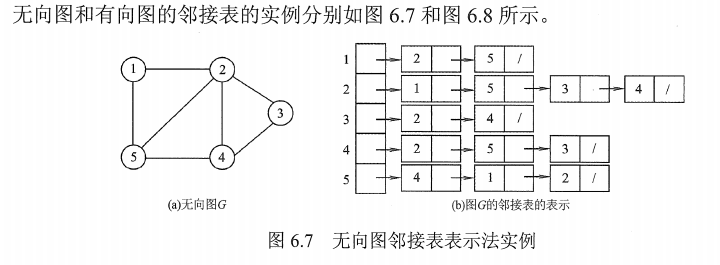
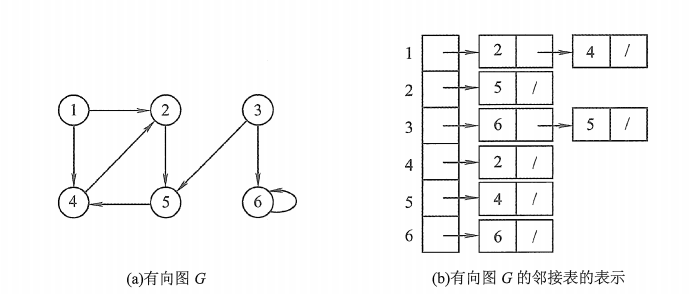
图的邻接表存储结构定义如下:

---

---

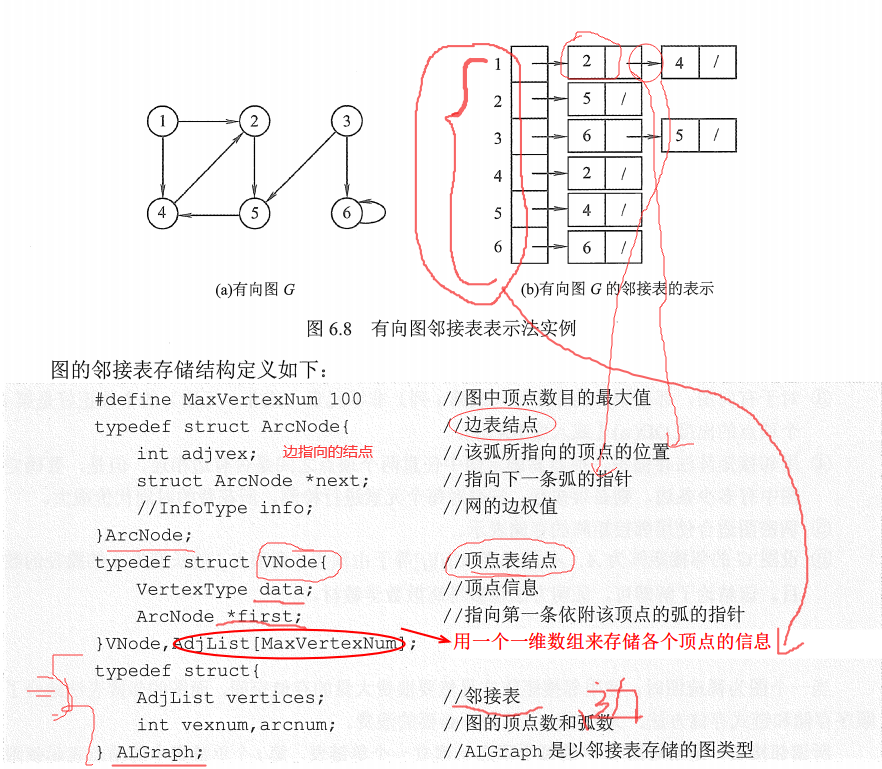
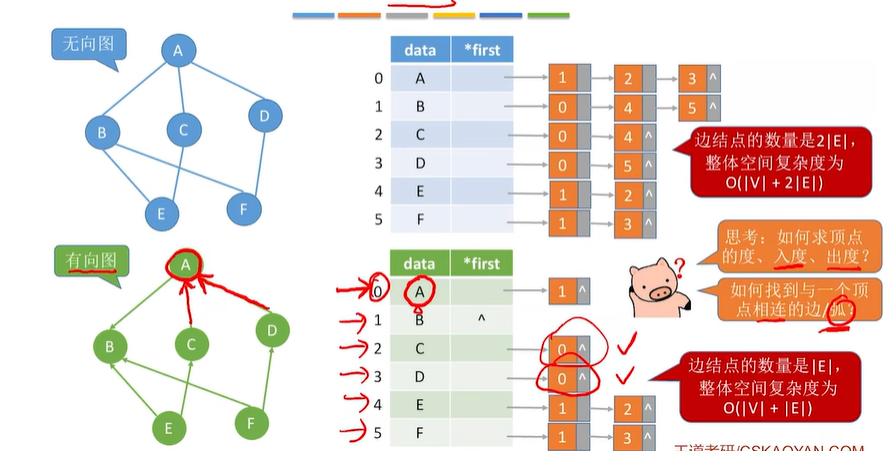
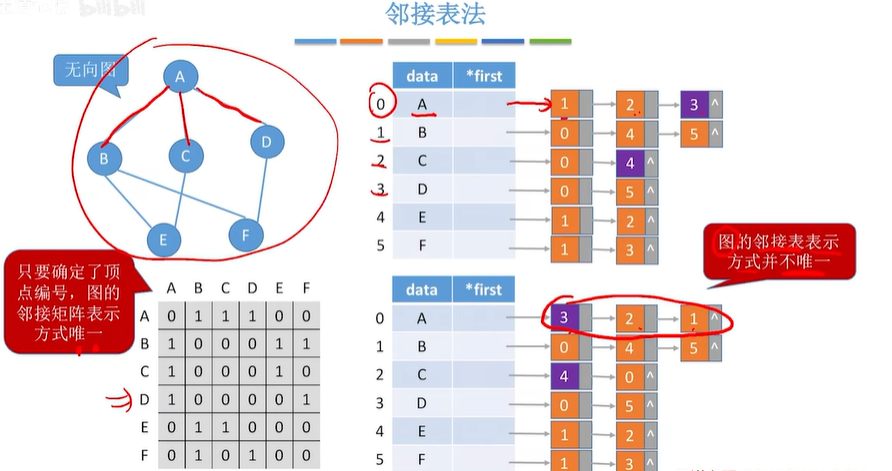
2.3 十字链表(存储有向图)

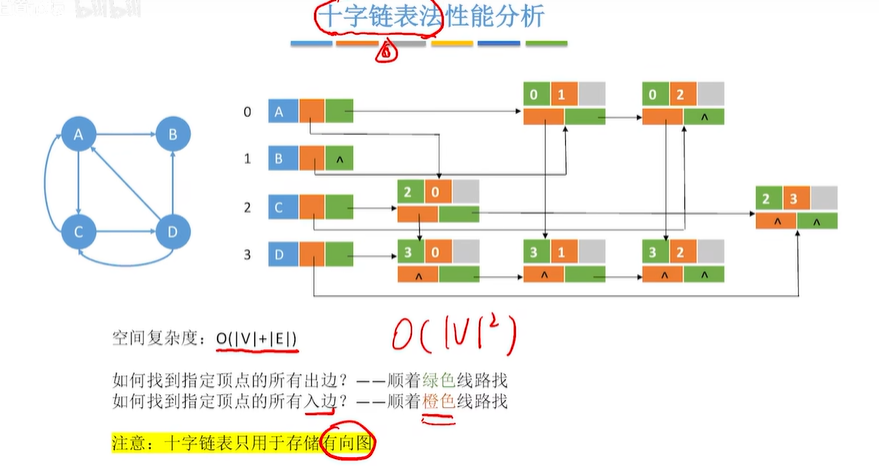
2.4 邻接多重表（存储无向图）

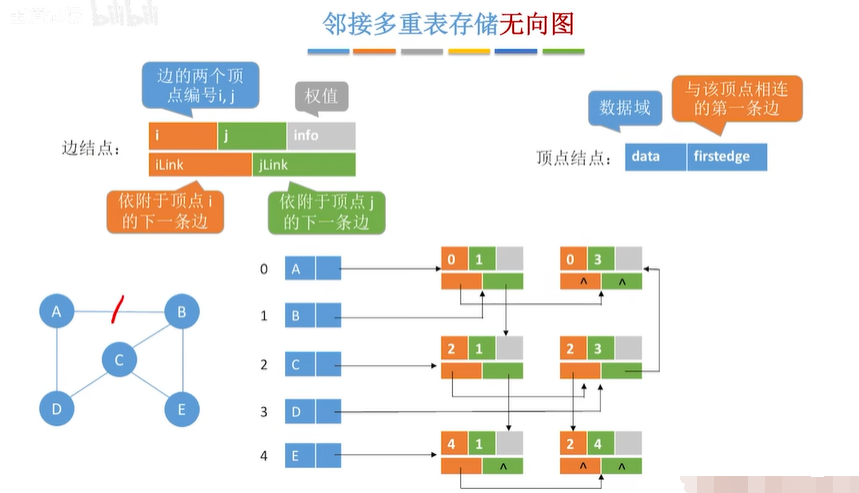
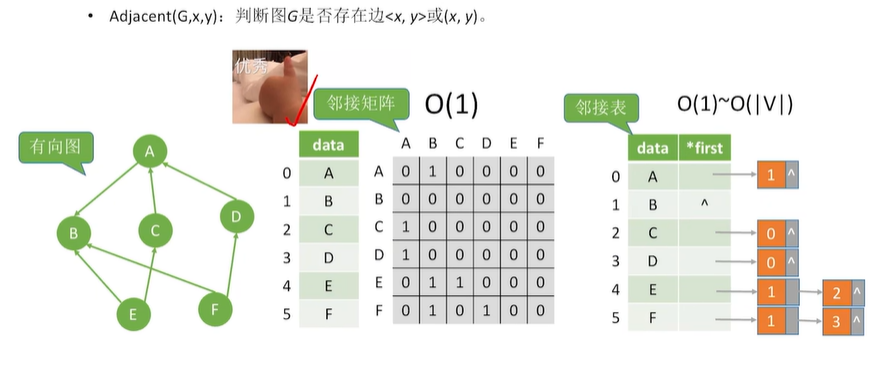
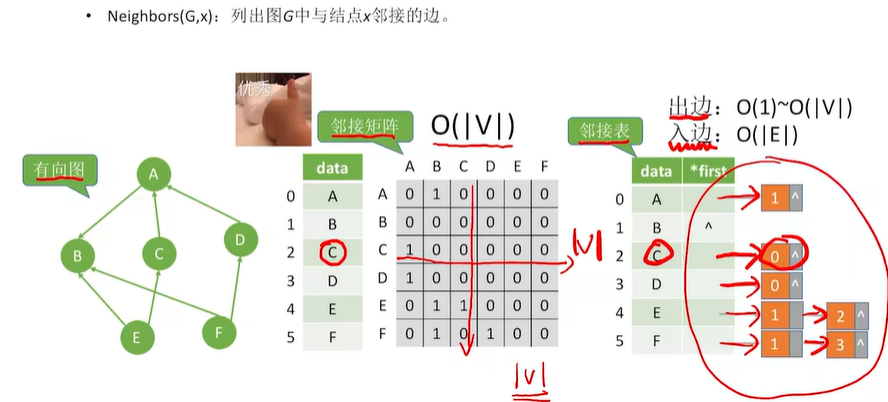
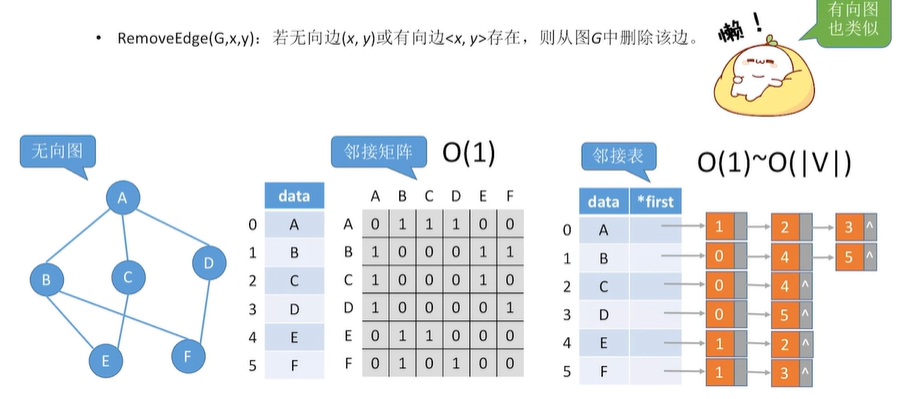
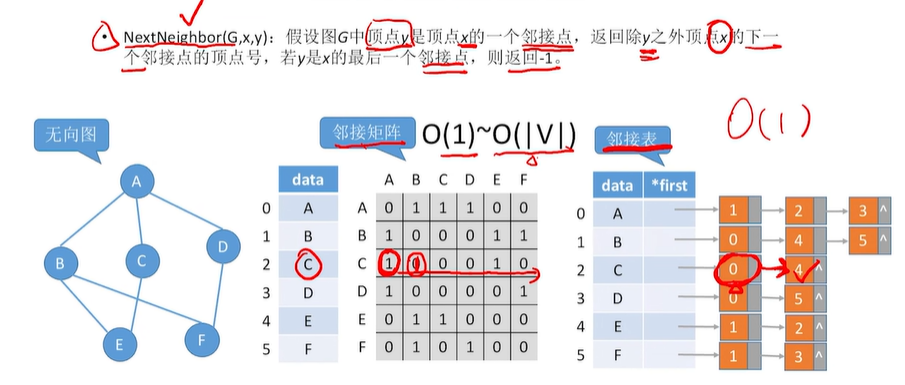
2.5 图的基本操作

教程：图的基本操作

---

---

---

---

---

---