数据结构-二叉树的前、中、后序遍历

news2024/10/7 5:30:53

目录

1. 二叉树的遍历

1.1 前序

1.2 中序

1.3 后序

1.4 遍历的复杂度

2.二叉树节点个数及高度的计算

2.1 二叉树节点个数

2.2 二叉树叶子节点的个数

2.3 二叉树高度

2.4 二叉树第k层节点个数

1. 二叉树的遍历

前面的章节中，我们学习了二叉树的顺序结构，二叉树除了顺序结构，还有链式结构，在学链式结构之前，要求深入掌握二叉树的结构，下面我们先来手动快速的创建一个简单的二叉树，方便学习，后面再来研究二叉树的真正创建的方式。

#include<stdio.h>
#include<stdlib.h>
#include<assert.h>

typedef int BTDataType;
typedef struct BinaryTreeNode
{
	BTDataType data;
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
}BTNode;

BTNode* BuyNode(BTDataType x)
{
	BTNode* node = (BTNode*)malloc(sizeof(BTNode));
	if (node == NULL)
	{
		perror("malloc fail\n");
		return NULL;
	}
	node->left = NULL;
	node->right = NULL;
	node->data = x;
	return node;
}

BTNode* CreatBinaryTree()
{
	BTNode* node1 = BuyNode(1);
	BTNode* node2 = BuyNode(2);
	BTNode* node3 = BuyNode(3);
	BTNode* node4 = BuyNode(4);
	BTNode* node5 = BuyNode(5);
	BTNode* node6 = BuyNode(6);

	node1->left = node2;
	node1->right = node4;
	node2->left = node3;
	node4->left = node5;
	node4->right = node6;
	return node1;
}

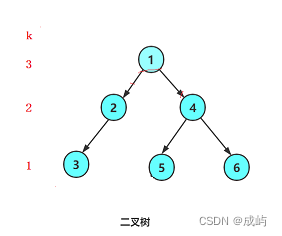
 下图就是我们上述代码创建的二叉树，从今天开始，我们看到二叉树要将其分为三个部分：根、左子树、右子树。

图中每个子树也能再分为根和左子树、右子树，直到不能再分为止。 

而二叉树的遍历分为：前序、中序、后序、层序。今天先来学习前中后序，层序后面再学。

1.1 前序

前序要求的访问次序：根、左子树、右子树。 

按照前序的访问规则，对上述代码的节点的访问次序依次是: 1 2 3 null null null 4 5 null null 6 null null。

先访问根节点1，然后访问它的左子树，左子树中先访问根节点2，然后访问2的左子树3，3的左右子树是null null，然后继续访问2的右子树为null，接着访问1的右子树，右子树中先访问根节点4，然后访问4的左子树5，再访问5的左右子树null null，接着访问4的右子树6,6的左右子树是null null，所以最终的访问次序是：1 2 3 null null null 4 5 null null 6 null null 

前序的代码实现：

//前序
void PrevOrder(BTNode* root)
{
	if (root==NULL)
	{
		printf("null ");
		return;
	}
	printf("%d ", root->data);
	PrevOrder(root->left);
	PrevOrder(root->right);
}

int main()
{
	BTNode* root = CreatBinaryTree();
	PrevOrder(root);
	printf("\n");
	return 0;
}

打印结果：

递归过程如下：

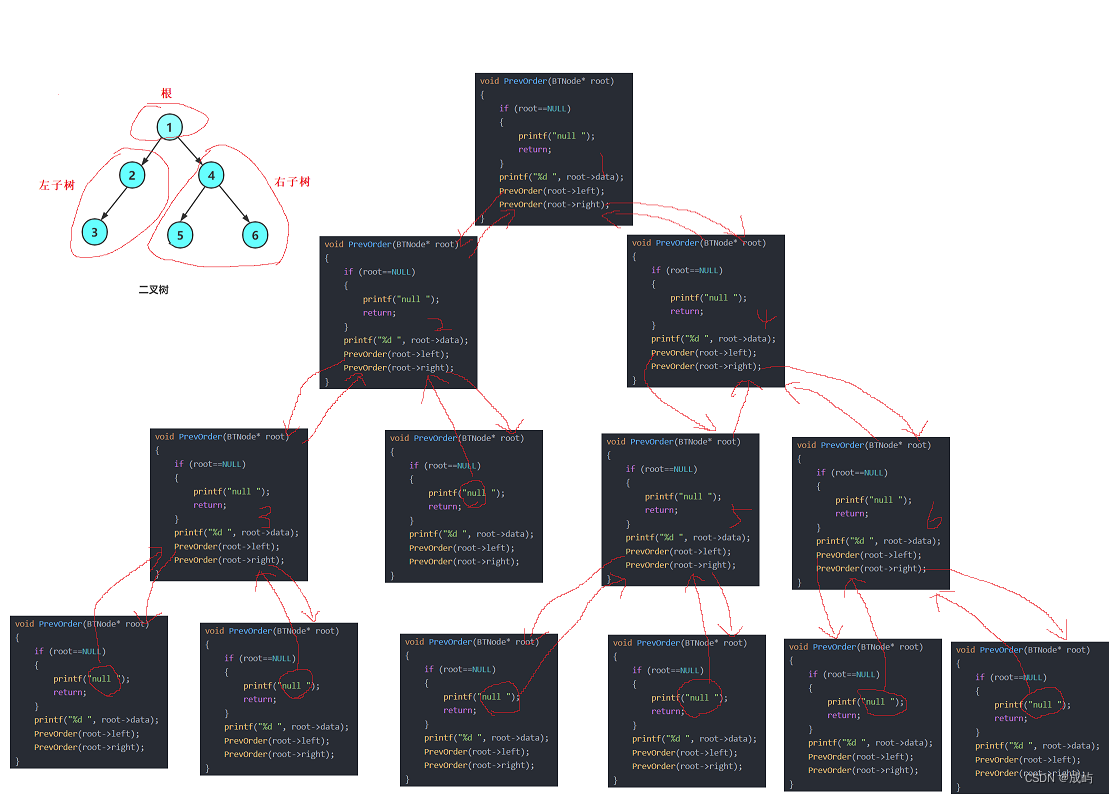
递归调用的过程实际就是函数栈帧的创建与销毁的过程，每次调用完左子树，它的栈帧就销毁了，调用右子树时会共用左子树的栈帧。

1.2 中序

中序要求的访问次序：左子树、根、右子树。

按照中序的访问规则，对上述代码中的节点的访问次序依次是：null 3 null 2 null 1 null 5 null 4 null 6 null。

因为每个子树都可以被拆成左子树、根和右子树，而且在访问时左子树的优先级高，左子树可以一直分到3，所以从3的左子树开始访问：null 3 null，然后把null 3 null作为2的左子树，再访问2和2的右子树：null 3 null 2 null，接着把 null 3 null 2 null 作为1的左子树，访问1和1的右子树......，最终访问的次序应该是：null 3 null 2 null 1 null 5 null 4 null 6 null。

中序代码实现：

//中序
void InOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("null ");
		return;
	}
	InOrder(root->left);
	printf("%d ", root->data);
	InOrder(root->right);
}

int main()
{
	BTNode* root = CreatBinaryTree();
	//前序
	PrevOrder(root);
	printf("\n");
	//中序
	InOrder(root);
	printf("\n");
	return 0;
}

运行结果：

1.3 后序

后序要求的访问次序：左子树、右子树、根。 

按照后序的访问规则，对上述代码中的节点的访问次序依次是：null null 3 null 2 null null 5 null null 6 4 1。 与分析前序和中序一样，这里不再详解。

后序代码实现:

//后序
void PostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("null ");
		return;
	}
	PostOrder(root->left);
	PostOrder(root->right);
	printf("%d ", root->data);
}
int main()
{
	BTNode* root = CreatBinaryTree();
	//前序
	PrevOrder(root);
	printf("\n");
	//中序
	InOrder(root);
	printf("\n");
	//后序
	PostOrder(root);
	printf("\n");
	return 0;
}

运行结果：

以上就是二叉树的前、中、后序遍历了，这几种方式其实就是对根的访问的先后问题，如果上述内容还不是很明白，最好画一下递归调用图，这样就很清楚了。

1.4 遍历的复杂度

时间复杂度：O(N)，因为二叉树一共有N个节点，递归一共调用N次，所以时间复杂度是O(N)。

空间复杂度：O(h),h的范围是：[ logN, N ]

为什么空间复杂度是这样的呢？

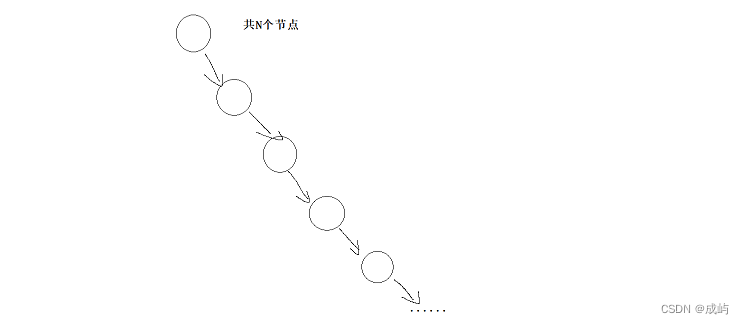
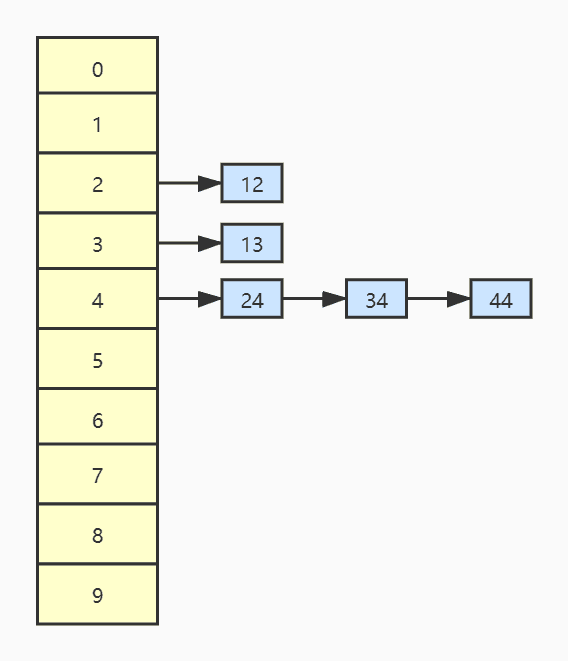
我们前面的章节中讲过，时间是一去不复返的，所以时间要累加计算，而空间是可以共用的，所以空间不能累加计算。我们在调用函数时，左子树调用完，它的栈帧会销毁，而调用右子树时，它会共用左子树的栈帧，而假设二叉树有N个节点，当它是满二叉树时，由于左右子树共用一个空间，只需创建空间logN次，而如果二叉树像下图中的情况，它就要创建空间N次，所以空间复杂度是:O(logN~N)

2.二叉树节点个数及高度的计算

2.1 二叉树节点个数

法一：

要计算二叉树节点个数，我们只需要将二叉树遍历一遍(前、中、后序都可以），每次调用时使size++即可，注意size要定义为全局变量，防止每次调用的时候size被置为0

代码如下：

//二叉树节点个数
int size = 0;
int BTreeSize(BTNode* root)
{
	if (root == NULL)
	{
		return;
	}
	size++;
	BTreeSize(root->left);
	BTreeSize(root->right);
}

int main()
{
	BTNode* root = CreatBinaryTree();
	BTreeSize(root);
	printf("BTreeSize:%d\n", size);
	return 0;
}

法二：

把计算节点个数分为，左子树节点个数+右子树节点个数+根节点个数，而每个子树还能分为左子树、右子树和根，所以我们使用递归的思想，如果根节点不为空，就分别计算它的左右子树节点个数+它自身，如果为空，就返回0。

代码如下：

//二叉树节点个数
int BTreeSize(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	return  BTreeSize(root->left) + BTreeSize(root->right)+1;
}

int main()
{
	BTNode* root = CreatBinaryTree();
	printf("BTreeSize:%d\n", BTreeSize(root));
	return 0;
}

运行结果：

2.2 二叉树叶子节点的个数

要计算叶子节点，也可以使用上述分开计算的方法，分别计算左子树和右子树的叶子节点个数，然后相加，递归的条件是：如果左子树和右子树的节点都是NULL，那说明是叶子节点，返回1，否则，说明是分支节点，继续往下递归。

代码如下：

//二叉树叶子节点
int BLeafNum(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	if (root->left == NULL && root->right == NULL)
	{
		return 1 ;
	}
	return BLeafNum(root->left) + BLeafNum(root->right);
}

int main()
{
	BTNode* root = CreatBinaryTree();
	printf("BLeafNum:%d\n", BLeafNum(root));
	return 0;
}

运行结果：

2.3 二叉树高度

 求二叉树高度，也可以分别求左子树和右子树的高度，然后比较大小，返回大的值，并将该值加一就是二叉树的高度，加一是因为左右子树距离根节点还有一层。

求左右子树的高度可以再分解为上面的步骤，所以使用递归解决问题。

代码如下：

//二叉树高度
int BTreeHeight(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	int LeftNum = BTreeHeight(root->left);
	int RightNum = BTreeHeight(root->right);
	return LeftNum > RightNum ? LeftNum + 1 : RightNum + 1;
}
int main()
{
	BTNode* root = CreatBinaryTree();
	printf(" BTreeHeight:%d\n", BTreeHeight(root));

	return 0;
}

 运行结果：

2.4 二叉树第k层节点个数

该问题可以转换成：分别求左子树的第k-1层和右子树的第k-1层，然后返回它们的和。

结束条件是：k==1 且k不为空。

比如我们要求1的第三层，就是求2和4的第二层，也就是求3 5 6的第一层

代码如下：

//二叉树第k层节点的个数
int BTreekNum(BTNode* root,int k)
{
	if (root == NULL)
	{
		return 0;
	}
	if (k == 1)
	{
		return 1;
	}
	return BTreekNum(root->left, k - 1) + BTreekNum(root->right, k - 1);
}
int main()
{
	BTNode* root = CreatBinaryTree();
	printf("BTreekNum:%d\n", BTreekNum(root,3));
	printf("BTreekNum:%d\n", BTreekNum(root, 2));
	return 0;
}

运行结果：

递归过程如下：

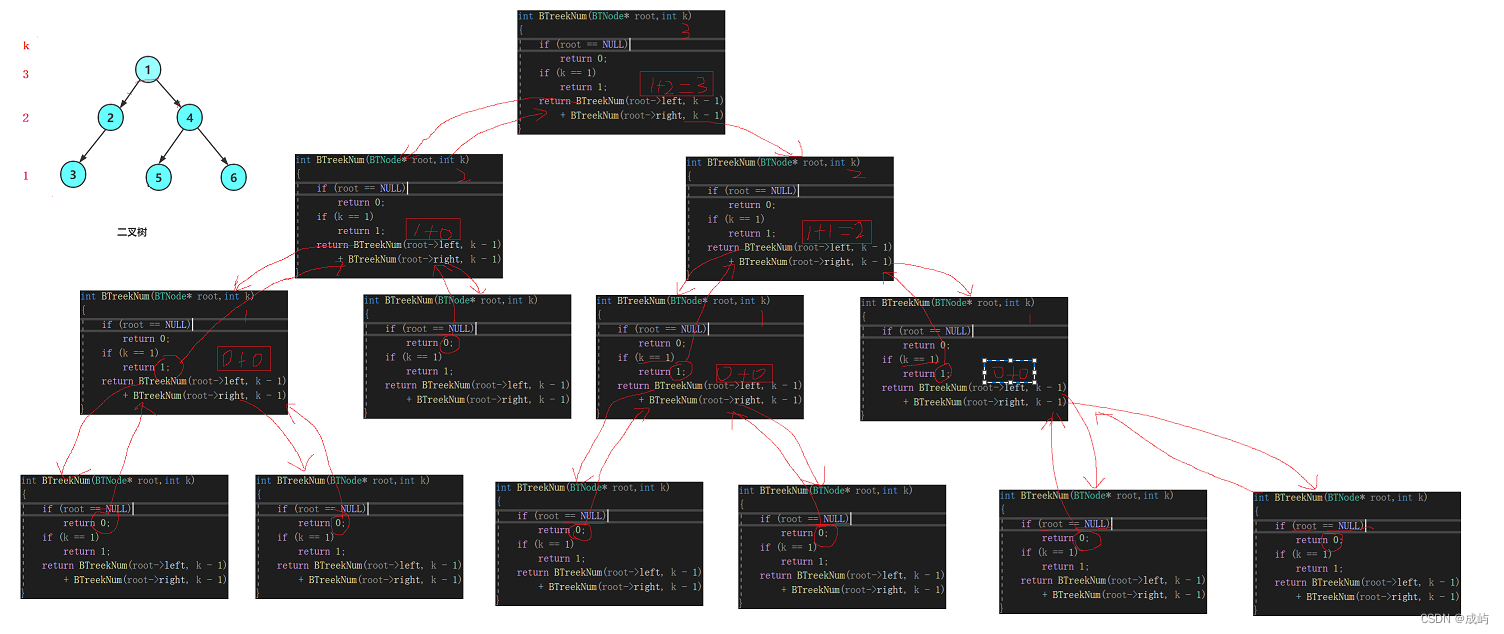
通过以上计算，相信我们对二叉树的遍历有了更深的理解，同时也加深了对递归的理解，其实当我们熟练运用递归之后，递归问题都可以分两步解决：1. 找出子问题  2. 递归条件。

 

以上就是今天学习的所有内容了，未完待续。。。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1208671.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

计算机毕业设计选题推荐-体育赛事微信小程序/安卓APP-项目实战

计算机毕业设计选题推荐-体育赛事微信小程序/安卓APP-项目实战

✨作者主页&#xff1a;IT毕设梦工厂✨ 个人简介&#xff1a;曾从事计算机专业培训教学&#xff0c;擅长Java、Python、微信小程序、Golang、安卓Android等项目实战。接项目定制开发、代码讲解、答辩教学、文档编写、降重等。 ☑文末获取源码☑ 精彩专栏推荐⬇⬇⬇ Java项目 Py…
阅读更多...
c语言11周（16~20）

c语言11周（16~20）

利用函数求和 //只填写要求的函数 double fun(int n) {double s 0;int i;for (i 1; i < n; i) {s 1.0 / (i * i);}return s; } 编写char fun(char c)函数&#xff0c;将数字参数字符c按如下规则转换。 题干编写char fun(char c)函数&#xff0c;将数字参数字符c按如…
阅读更多...
【milkv】1、光感bh1750驱动添加及测试

【milkv】1、光感bh1750驱动添加及测试

前言 本章介绍在milkv-duo开发板上添加光感bh1750&#xff0c;并实现应用层测试。 一、电路图查看 1.1 duo开发板i2c引脚 https://github.com/milkv-duo/duo-files 这些都是可以作为i2c使用的引脚 注意&#xff1a;电路图中的gpio0、1对应的是芯片上的gpio28、29&#…
阅读更多...
为什么Springboot项目中有些写法继承了SpringBootServletInitializer类？Springboot的两种发布方式

为什么Springboot项目中有些写法继承了SpringBootServletInitializer类？Springboot的两种发布方式

文章目录 一、前言二、SpringBoot的两种发布方式2.1、内置容器运行2.2、外置容器&#xff08;Tomcat&#xff09;运行 三、扩展3.1、如何将 Spring Boot 项目打包成 war 包&#xff1f; 一、前言 在一次SpringBoot源码中看到了启动类中继承了SpringBootServletInitializer&…
阅读更多...
EMC-4641C运动控制器固件升级

EMC-4641C运动控制器固件升级

EMC-4641C运动控制器固件升级 更新前查看运动控制器固件版本 点击打开ESMTPTest_X64R.exe程序 点击搜索&#xff0c;程序自动选择IP为192.168.0.135的运动控制器&#xff08;实际操作时候可能会因为现场情况&#xff0c;IP会有细微不同&#xff09; 点击Connest 等待几秒后在…
阅读更多...
『数据结构与算法』散列表（哈希表）

『数据结构与算法』散列表（哈希表）

1. 什么是散列表 散列表&#xff08;Hash Table&#xff09;也叫哈希表&#xff0c;是根据给定关键字&#xff08;Key&#xff09;来计算出该关键字在表中存储地址的数据结构。也就是说&#xff0c;散列表建立了关键字与存储地址之间的一种直接映射关系&#xff0c;将关键字映…
阅读更多...
【电路笔记】-诺顿定理（Norton‘s Theorem）

【电路笔记】-诺顿定理（Norton‘s Theorem）

诺顿定理&#xff08;Norton’s Theorem&#xff09; 文章目录 诺顿定理&#xff08;Nortons Theorem&#xff09;1、概述与定义2、诺顿模型确定3、一些线性电路的诺顿模型3.1 单电压源3.2 单电流源3.3 多电流/电压源 5、总结 本文是我们上一篇有关戴维南定理的文章的延续。 在…
阅读更多...
[文件读取]lanproxy 文件读取 （CVE-2021-3019）

[文件读取]lanproxy 文件读取 （CVE-2021-3019）

1.1漏洞描述 漏洞编号CVE-2021-3019漏洞类型文件读取漏洞等级⭐漏洞环境VULFOCUS攻击方式 描述: Lanproxy 路径遍历漏洞通过../绕过读取任意文件。该漏洞允许目录遍历读取/../conf/config.properties来获取到内部网连接的凭据。 1.2漏洞等级 高危 1.3影响版本 Lanproxy 1.4漏洞…
阅读更多...
酷柚易汛ERP-购货订单操作指南

酷柚易汛ERP-购货订单操作指南

1、应用场景 先下购货订单&#xff0c;收货入库后生成购货单。 2、主要操作 2.1 新增购货订单 打开【购货】-【购货订单】新增购货订单。&#xff08;*为必填项&#xff0c;其他为选填&#xff09; ① 录入供应商&#xff1a;点击供应商字段框的 &#xff0c;在弹框中选择供…
阅读更多...
漏洞-任意账号注册

漏洞-任意账号注册

一漏洞介绍 1.未验证邮箱/手机号 情景&#xff1a;应用为了方便用户记录用户名&#xff0c;使用邮箱和手机号作为用户名&#xff08;因此很多应用在注册的时候就要求用户填写&#xff0c;多数时候都会给用户发送激活信息&#xff0c;激活后才能登录&#xff09; 缺陷&#xff…
阅读更多...
Linux Mint 21.3 将搭载 Cinnamon 6.0 和实验性 Wayland 支持

Linux Mint 21.3 将搭载 Cinnamon 6.0 和实验性 Wayland 支持

导读Wayland 会话可能在 Linux Mint 23 系列中成为默认选项&#xff0c;预计将在 2026 年实现。 Linux Mint 项目今天在他们的每月新闻通讯中 宣布&#xff0c;他们已经开始着手在未来的 Linux Mint 发行版中实施 Wayland 会话&#xff0c;最初将在 Linux Mint 21.3 中提供。 …
阅读更多...
3DMAX建模基础教程：常用工具补充

3DMAX建模基础教程：常用工具补充

在本篇3DMAX建模基础教程中&#xff0c;我们将为您介绍一些常用的工具及其功能。熟练掌握这些工具将大大提高您的建模效率。 1️⃣ 选择与变换工具 选择工具&#xff1a;帮助您选择对象&#xff0c;可以通过单击对象或按组选择。 变换工具&#xff1a;对选定的对象进行移动、…
阅读更多...
【milkv】0、duo编译环境搭建

【milkv】0、duo编译环境搭建

一、开发资料整理 Docker https://hub.docker.com/repository/docker/dreamcmi/cv1800-docker/general GitHub https://github.com/milkv-duo/duo-buildroot-sdk CV181x/CV180x MMF SDK 开发文档汇总 https://developer.sophgo.com/thread/471.html cv181x芯片使用的交叉…
阅读更多...
【计算机网络】UDP协议

【计算机网络】UDP协议

UDP的结构 我们学习一个协议最主要的就是理解它的报文格式&#xff0c;对于UDP协议来说 我们看下面的这张图。 16位UDP长度&#xff0c;表示整个数据报&#xff08;UDP首部UDP数据&#xff09;的最大长度。UDP报文长度占两个字节&#xff0c;16位表示的数据范围&#xff08;0-…
阅读更多...
新版本Idea设置启动参数

新版本Idea设置启动参数

1.进入配置页面 2.点击下图红框的部分&#xff0c;会看到有很多操作可选 3.选择添加VM参数即可 此时就会多出一个可以输入参数的框了&#xff0c;如下&#xff1a;
阅读更多...
一个破单机，也要用远程缓存？

一个破单机，也要用远程缓存？

大家好&#xff0c;豆小匠终于开始Coding了&#xff0c;这期来聊聊实战相关的杂谈。 正文开始&#xff01; 作为编程萌新的时候&#xff0c;总想着把程序做复杂&#xff0c;堆技术栈。 但是程序是为场景服务的&#xff0c;比如&#xff0c;我想提高接口的响应速度&#xff0c…
阅读更多...
酷柚易汛ERP- 组装单与拆卸单操作

酷柚易汛ERP- 组装单与拆卸单操作

1、功能介绍 组装单用来处理企业组装等加工业务&#xff0c;拆卸单用来处理企业拆卸等加工业务&#xff0c;支持一对多的产品加工业务。 2、主要操作 2.1 新增组装单 打开【仓库】-【组装单】新增组装单。 录入组合件与子件&#xff0c;单据审核后&#xff0c;系统根据存货…
阅读更多...
如何在Qemu上跑Milk-duo开发板

如何在Qemu上跑Milk-duo开发板

前言 &#xff08;1&#xff09;PLCT实验室实习生长期招聘&#xff1a;招聘信息链接 &#xff08;2&#xff09;学习本文之前&#xff0c;要求先看一下Milk-V Duo快速上手的环境搭建部分&#xff0c;创建好镜像文件。 正文 编译milk-duo qemu &#xff08;1&#xff09;下面步…
阅读更多...
【STM32/FreeRTOS】SysTick定时器及FreeRTOS系统节拍

【STM32/FreeRTOS】SysTick定时器及FreeRTOS系统节拍

目录 一、SysTick定时器 1、SysTick寄存器介绍 &#xff08;1&#xff09;控制及状态寄存器 &#xff08;2&#xff09;重装载数值寄存器 &#xff08;3&#xff09;当前数值寄存器 2、SysTick寄存器配置函数 二、FreeRTOS中的SysTick定时器 1、SysTick配置函数及分析 …
阅读更多...
个人Typora存储图片专用

个人Typora存储图片专用

阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023