目录
- 0 专栏介绍
- 1 差速模型定义
- 2 控制量与驱动量
- 3 运动学方程
- 4 仿真实现
- 4.1 Python仿真
- 4.2 Matlab仿真
0 专栏介绍
🔥附C++/Python/Matlab全套代码🔥课程设计、毕业设计、创新竞赛必备!详细介绍全局规划(图搜索、采样法、智能算法等);局部规划(DWA、APF等);曲线优化(贝塞尔曲线、B样条曲线等)。
🚀详情:图解自动驾驶中的运动规划(Motion Planning),附几十种规划算法
1 差速模型定义
差速轮式移动机器人是一种机器人平台,其运动控制基于两个或多个并行但独立驱动的轮子。这些轮子通常位于机器人的两侧,通过分别控制每个轮子的速度和方向,机器人能够实现灵活的运动和转向。

差速轮式移动机器人的核心是通过调整两个轮子的速度差异,使其能够前进、后退、转向、旋转等。这种设计使得差速轮式移动机器人在室内和室外环境中都能够有效地导航和执行各种任务,如物品搬运、勘探、巡逻等。
差速轮式移动机器人的经典结构如图所示
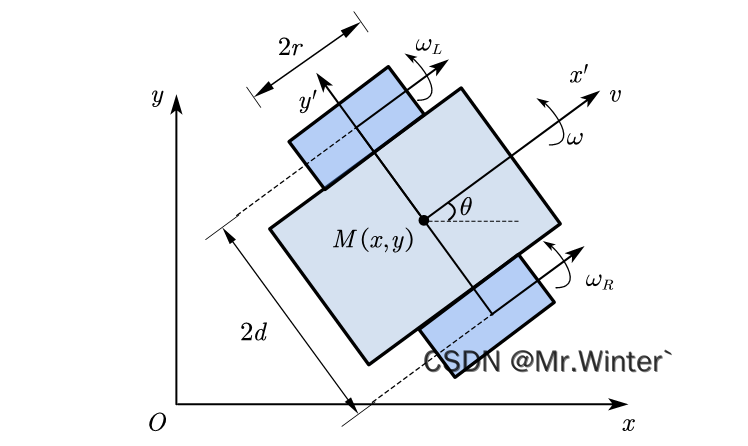
此模型中设移动机器人的几何中心和质心重合,且重合点在轮轴中点上。用 p = [ x y θ ] T \boldsymbol{p}=\left[ \begin{matrix} x& y& \theta\\\end{matrix} \right] ^T p=[xyθ]T表示该移动机器人在全局坐标系 x O y xOy xOy中的位姿, M ( x , y ) M\left( x,y \right) M(x,y)表示该移动机器人质心在全局坐标系的坐标。设移动机器人车轮直径为 2 r 2r 2r,两驱动轮间距为 2 d 2d 2d
设移动机器人局部坐标系为 x ′ O y ′ x'Oy' x′Oy′,则定义机器人瞬时线速度 v v v为其沿 x ′ x' x′轴(亦即前进方向)的速度,位姿角 θ \theta θ为 x ′ x' x′轴与全局坐标系 x x x轴的夹角,角速度 ω \omega ω为 x ′ x' x′轴绕 M M M点的瞬时旋转角速率,整个系统以 u = [ v ω ] T \boldsymbol{u}=\left[ \begin{matrix} v& \omega\\\end{matrix} \right] ^T u=[vω]T为输入控制量。设 ω L \omega _L ωL、 ω R \omega _R ωR及 v L v_L vL、 v R v_R vR分别为机器人左右驱动轮的角速度、线速度,也为驱动量。
2 控制量与驱动量
下面考察控制量与驱动量间的关系,首先有
v = v L + v R 2 v=\frac{v_L+v_R}{2} v=2vL+vR
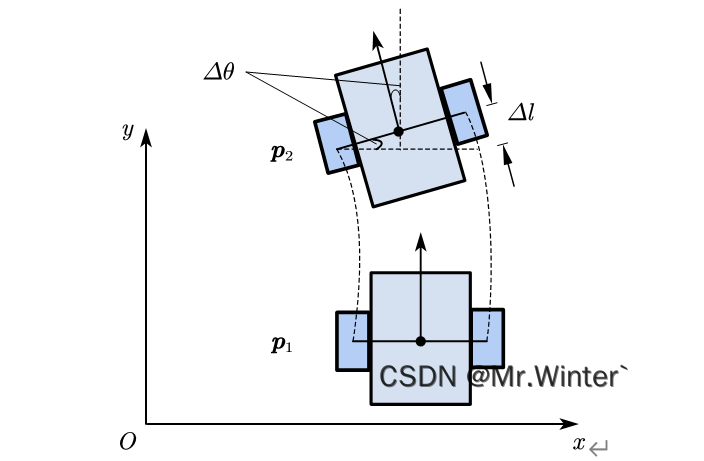
如图所示,设在时间 Δ t → 0 \varDelta t\rightarrow 0 Δt→0内,机器人由位姿 p 1 \boldsymbol{p}_1 p1移动到位姿 p 2 \boldsymbol{p}_2 p2,位姿角 θ \theta θ变化了 Δ θ \varDelta \theta Δθ,一轮比另一轮多运动了 Δ l = ( v R − v L ) Δ t \varDelta l=\left( v_R-v_L \right) \varDelta t Δl=(vR−vL)Δt,则 Δ θ ≈ sin Δ θ = Δ l / ( 2 d ) \varDelta \theta \approx \sin \varDelta \theta ={{\varDelta l}/{\left( 2d \right)}} Δθ≈sinΔθ=Δl/(2d),从而
ω = Δ θ Δ t = v R − v L 2 d \omega =\frac{\varDelta \theta}{\varDelta t}=\frac{v_R-v_L}{2d} ω=ΔtΔθ=2dvR−vL
进而得到机器人运动半径
r = v ω = v R + v L v R − v L d r=\frac{v}{\omega}=\frac{v_R+v_L}{v_R-v_L}d r=ωv=vR−vLvR+vLd
所以控制量与驱动量的关系用矩阵表示为:
[ v ω ] = [ 1 2 1 2 1 2 d − 1 2 d ] [ v R v L ] \left[ \begin{array}{c} v\\ \omega\\\end{array} \right] =\left[ \begin{matrix} \frac{1}{2}& \frac{1}{2}\\ \frac{1}{2d}& -\frac{1}{2d}\\\end{matrix} \right] \left[ \begin{array}{c} v_R\\ v_L\\\end{array} \right] [vω]=[212d121−2d1][vRvL]
3 运动学方程
差速移动机器人的运动学方程容易得到
p ˙ = [ x ˙ y ˙ θ ˙ ] = [ cos θ 0 sin θ 0 0 1 ] [ v ω ] = S ( q ) u \boldsymbol{\dot{p}}=\left[ \begin{array}{c} \dot{x}\\ \dot{y}\\ \dot{\theta}\\\end{array} \right] =\left[ \begin{matrix} \cos \theta& 0\\ \sin \theta& 0\\ 0& 1\\\end{matrix} \right] \left[ \begin{array}{c} v\\ \omega\\\end{array} \right] =S\left( \boldsymbol{q} \right) \boldsymbol{u} p˙= x˙y˙θ˙ = cosθsinθ0001 [vω]=S(q)u
也可以根据控制量和驱动量的关系进一步写出
p ˙ = [ x ˙ y ˙ θ ˙ ] = [ cos θ 0 sin θ 0 0 1 ] [ 1 2 1 2 1 2 d − 1 2 d ] [ v R v L ] = S ~ ( q ) u \boldsymbol{\dot{p}}=\left[ \begin{array}{c} \dot{x}\\ \dot{y}\\ \dot{\theta}\\ \end{array} \right] =\left[ \begin{matrix} \cos \theta& 0\\ \sin \theta& 0\\ 0& 1\\ \end{matrix} \right] \left[ \begin{matrix} \frac{1}{2}& \frac{1}{2}\\ \frac{1}{2d}& -\frac{1}{2d}\\ \end{matrix} \right] \left[ \begin{array}{c} v_R\\ v_L\\ \end{array} \right] =\tilde{S}\left( \boldsymbol{q} \right) \boldsymbol{u} p˙= x˙y˙θ˙ = cosθsinθ0001 [212d121−2d1][vRvL]=S~(q)u
由上式可知自主移动机器人是状态向量维数为3,但控制输入量为2维的非完整约束系统,因此自主移动机器人存在无法全向移动的运动约束,在路径规划中需要协调路径平滑与连续性。
4 仿真实现
4.1 Python仿真
核心的运动学迭代公式实现如下
def lookforward(self, state: np.ndarray, u: np.ndarray, dt: float) -> np.ndarray:
F = np.array([[1, 0, 0, 0, 0],
[0, 1, 0, 0, 0],
[0, 0, 1, 0, 0],
[0, 0, 0, 0, 0],
[0, 0, 0, 0, 0]])
B = np.array([[dt * math.cos(state[2]), 0],
[dt * math.sin(state[2]), 0],
[ 0, dt],
[ 1, 0],
[ 0, 1]])
new_state = F @ state + B @ u
return new_state

4.2 Matlab仿真
核心的运动学迭代公式实现如下
function robot = f(robot, u, dt)
%@breif: robotic kinematic
F = [ 1 0 0 0 0
0 1 0 0 0
0 0 1 0 0
0 0 0 0 0
0 0 0 0 0];
B = [dt * cos(robot.theta) 0
dt * sin(robot.theta) 0
0 dt
1 0
0 1];
x = [robot.x; robot.y; robot.theta; robot.v; robot.w];
x_star = F * x + B * u';
robot.x = x_star(1); robot.y = x_star(2); robot.theta = x_star(3);
robot.v = x_star(4); robot.w = x_star(5);
end

完整工程代码请联系下方博主名片获取
🔥 更多精彩专栏:
- 《ROS从入门到精通》
- 《Pytorch深度学习实战》
- 《机器学习强基计划》
- 《运动规划实战精讲》
- …