本文,我们主要讲解一些适合用C++的数据结构来求解的二叉树问题,其中涉及了二叉树的遍历,栈和队列等数据结构,递归与回溯等知识,希望可以帮助你进一步理解二叉树。

目录
1.二叉树的层序遍历
2.二叉树的公共祖先
3.二叉搜索树与双向链表
4.二叉树的创建(前序+中序,后序+中序)
前序+中序:
中序+后序:
5.二叉树的三种迭代法遍历
1.二叉树的层序遍历
题目链接:二叉树的层序遍历
思路分析:
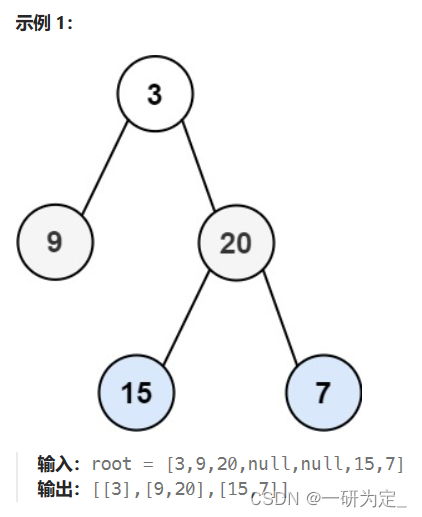
这个题目的难点是如何控制层序遍历的同时还能保持入队操作,我们知道,二叉树的的层序遍历一般和队列联系在一起使用,包括一些bfs的习题也经常以队列、栈作为遍历的容器,本题,我们需要思考如何能够遍历某一层的同时,将该层的下一层的节点保存下来,同时还需要将该层的节点按从左到右的顺序输出,显然,我们需要将每一层的节点聚在一起保存,这样才能保证输出的正确性,我们可以提供一个输出的变量len,表示该层需要输出几个节点,然后将该层的节点输出的同时把它的左右孩子都入队,这样一来,就能保证每一层的节点都聚在一起并且按从左到右的顺序排列,之后保存输出即可。
AC代码:
class Solution {
public:
queue<TreeNode*> q;
vector<vector<int>> ans;
vector<vector<int>> levelOrder(TreeNode* root) {
if(!root)
return ans;
vector<int> cot;
q.push(root);
int len=1;
while(!q.empty())
{
while(len--)
{
TreeNode* tmp=q.front();
q.pop();
if(tmp->left!=nullptr) q.push(tmp->left);
if(tmp->right!=nullptr) q.push(tmp->right);
cot.push_back(tmp->val);
}
len=q.size();
ans.push_back(cot);
cot.clear();
}
return ans;
}
};2.二叉树的公共祖先
题目链接:二叉树的公共祖先
思路分析:
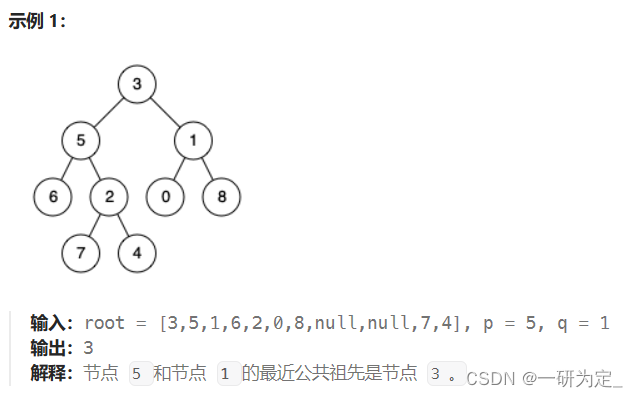
难点在于如何在找到两个节点的条件下,回溯双方的祖先节点来确定最近公共祖先,这里仅提供其中一个思路,我们可以保存寻找路径,然后让两个路径中较长的路径(也就是离公共祖先节点较远的)逐渐向上走,直到两条路径交合,交合点就是最近公共祖先。
class Solution {
public:
bool isexist(TreeNode*root,TreeNode *key)
{
if(root==nullptr)
return false;
else if(root==key)
return true;
else
return isexist(root->left,key)||isexist(root->right,key);
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
stack<TreeNode*>ppath;
stack<TreeNode*>qpath;
TreeNode*cur=root;
ppath.push(root);
qpath.push(root);
//寻找p的路径
while(cur)
{
if(cur==p)
break;
else if(isexist(cur->left,p))
{
ppath.push(cur->left);
cur=cur->left;
}
else if(isexist(cur->right,p))
{
ppath.push(cur->right);
cur=cur->right;
}
}
//寻找q的路径
cur=root;
while(cur)
{
if(cur==q)
break;
else if(isexist(cur->left,q))
{
qpath.push(cur->left);
cur=cur->left;
}
else if(isexist(cur->right,q))
{
qpath.push(cur->right);
cur=cur->right;
}
}
//开始寻找
TreeNode *ans=nullptr;
while(ppath.size()&&qpath.size())
{
if(ppath.size() > qpath.size())
ppath.pop();
else if(ppath.size() < qpath.size())
qpath.pop();
else if(ppath.size() == qpath.size())
{
if(ppath.top()==qpath.top())
{
ans=ppath.top();
break;
}
else
{
ppath.pop();
qpath.pop();
}
}
}
return ans;
}
};3.二叉搜索树与双向链表
题目链接:二叉搜索树与双向链表
思路分析:
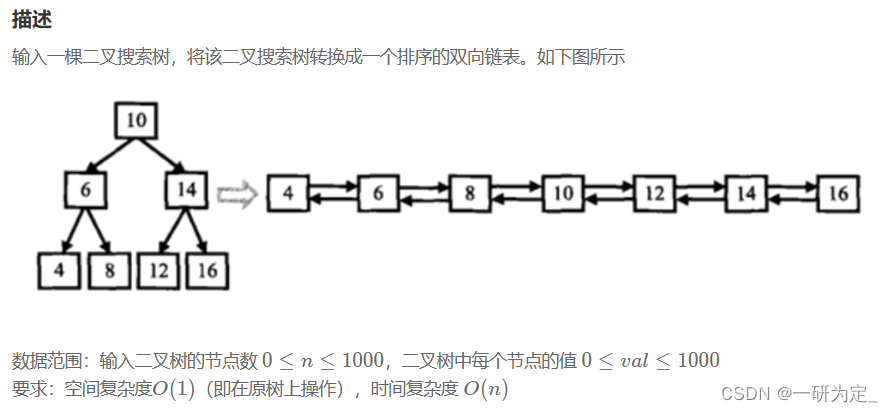

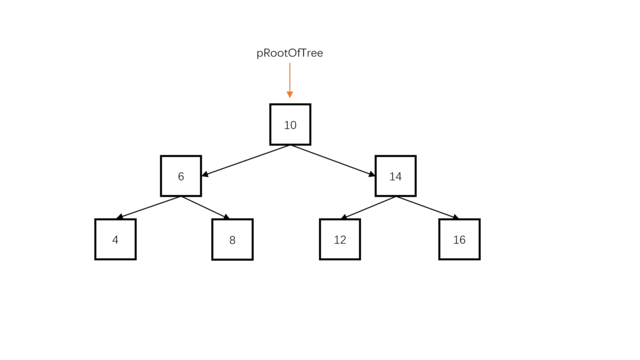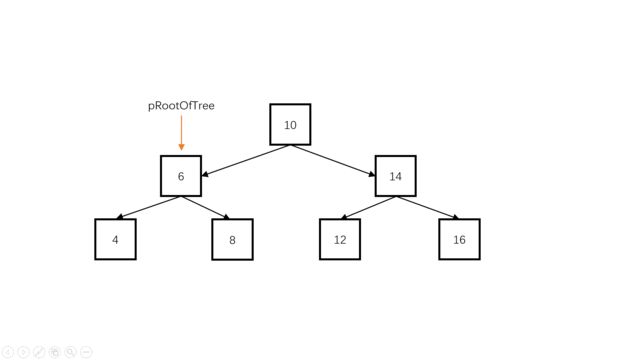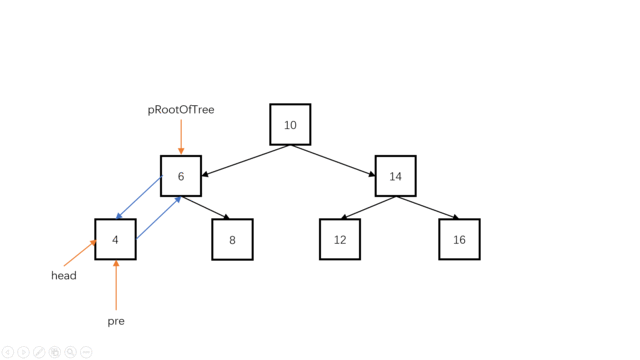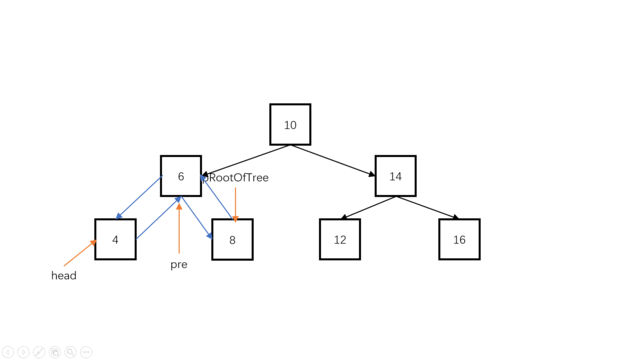
本体的难点在于,如何在原树上做修改而不影响接下来的操作,当然,暴力也可以做,但是这里要求我们在原树上直接做修改,所以,这里不解释暴力做法,我们就按题目规定的思路来,我们知道,二叉搜索树最左端的元素一定最小,最右端的元素一定最大,因此二叉搜索树的中序遍历就是一个递增序列,我们只要对它中序遍历就可以组装成为递增双向链表。
我们可以使用一个指针pre指向当前结点root的前继。(例如root为指向10的时候,preNode指向8),对于当前结点root,有root->left要指向前继pre(中序遍历时,对于当前结点root,其左孩子已经遍历完成了,此时root->left可以被修改。);同时,pr->right要指向当前结点(当前结点是pre的后继),此时对于pre结点,它已经完全加入双向链表。
class Solution {
public:
TreeNode *head=nullptr;
TreeNode*pre=nullptr;
TreeNode* Convert(TreeNode* pRootOfTree) {
if(pRootOfTree==nullptr)
return nullptr;
Convert(pRootOfTree->left);//找到最左节点,也就是最小的那个点
if(head==nullptr)//此时是第一个最小值,也就是头结点
{
head=pRootOfTree;
pre=pRootOfTree;
}
else
{
pre->right=pRootOfTree;
pRootOfTree->left=pre;
pre=pRootOfTree;
}
Convert(pRootOfTree->right);
return head;
}
};
4.二叉树的创建(前序+中序,后序+中序)
这应该算是一个老生常谈的问题了,算是经典中的经典了,其实不论是前序+中序还是后序+中序,其原理都大同小异,所以,我们将这两个例子放在一起讲解,有助于理解和记忆。
题目链接:105. 从前序与中序遍历序列构造二叉树 - 力扣(LeetCode)
106. 从中序与后序遍历序列构造二叉树 - 力扣(LeetCode)
思路分析:
前序+中序:
递归法:
只要我们在中序遍历中定位到根节点,那么我们就可以分别知道左子树和右子树中的节点数目。由于同一颗子树的前序遍历和中序遍历的长度显然是相同的,因此我们就可以对应到前序遍历的结果中,也就是每次都从中序遍历中寻找根节点,然后通过中序遍历将左右子树划分开来,再递归构造新的左右子树即可;
class Solution {
public:
TreeNode *root=nullptr;
TreeNode* build(vector<int>& pre, vector<int>& in,int pl,int pr,int il,int ir)
{
if(pl>pr)//如果越界直接返回空即可
return nullptr;
TreeNode* cur=new TreeNode(pre[pl]);//前序遍历第一个元素一定是某棵子树的根节点
int idx=0,len=0;//分别表示根节点在中序遍历的位置和左子树的节点个数
for(int i=il;i<=ir;i++)
{
if(in[i]==pre[pl]) //找到根节点所在的中序遍历的位置以确定根的左右子树
{
idx=i;
len=i-il;//找到对应的左子树的节点个数
break;
}
}
cur->left=build(pre,in,pl+1,pl+len,il,idx-1);
cur->right=build(pre,in,pl+1+len,pr,idx+1,ir);
return cur;
}
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
root= build(preorder,inorder,0,preorder.size()-1,0,inorder.size()-1);
return root;
}
};迭代法:
我们先来假设一种极端情况,如果一棵二叉树只有左孩子,那么其结构就类似于一张单链表,它的前序遍历和中序遍历一定就相反,我们将这个由此就可以判断此之前的过程中的每一个节点都没有右孩子,为了便于理解,我们用例子加以说明:
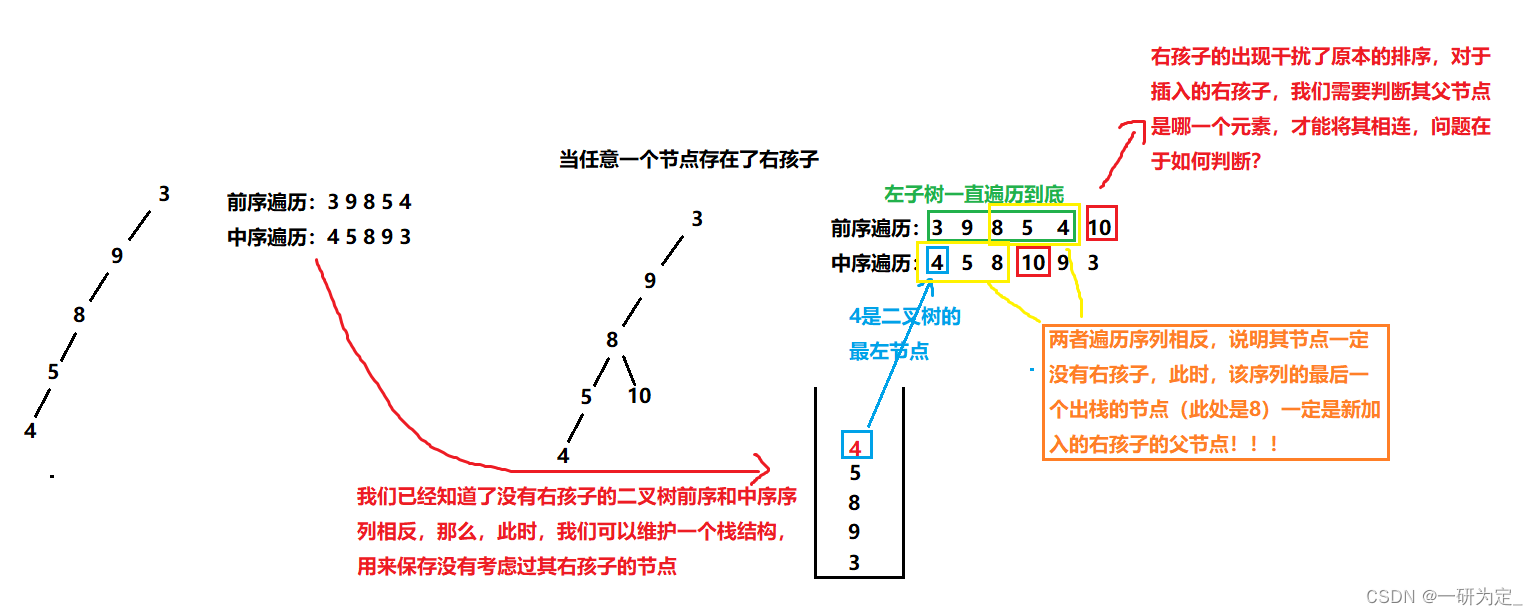
那么此时我们就可以维护一个栈,用来保存还没有考虑过右孩子的节点,按前序遍历的序列一直向二叉树的左端去遍历,当某个时刻遍历到了二叉树的最左节点,此时说明前序遍历的下一个元素一定是栈中某个节点的右孩子了,然后我们再依次对比栈中元素和中序序列,取出栈中的最后一个满足前序和中序序列相反的元素,将新加入的节点加入其右孩子,再将其入栈,我们无需再考虑已经出栈的元素,因为他们的右子树都已经被考虑完了,所以其树结构已经形成了,重复该过程直到前序序列遍历完毕即可形成一棵完整的树。
class Solution {
public:
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
if(!preorder.size())
return nullptr;
TreeNode *root=new TreeNode(preorder[0]);//先序遍历的第一个节点一定是根
stack<TreeNode*>st;
st.push(root);
int idx=0;//初始idx指向中序遍历的第一个元素(整棵二叉树的最左节点)
for(int i=1;i<preorder.size();i++)//根节点已经加入,所以前序遍历从下标1开始即可
{
TreeNode* node=st.top();
if(node->val!=inorder[idx])//如果加入节点还没判断是不是有右孩子
{
node->left=new TreeNode(preorder[i]);
st.push(node->left);//节点入栈等待判断
}
else //此时说明已经到达了某棵子树的最左节点,开始判断新加入的节点(preorder[i])是哪一个栈中节点的右孩子
{
TreeNode* parent=nullptr;
while(!st.empty()&& st.top()->val==inorder[idx]) //前中序遍历序列一致,此时该节点没有右孩子
{
parent=st.top();//最后一个出栈的节点一定是那个父节点,用于保存上次出栈记录
st.pop();
++idx;
}
parent->right=new TreeNode(preorder[i]);//创建其右孩子
st.push(parent->right);//不能忘了将新创建的节点加入,因为该节点可能还有左右子树需要创建
}
}
return root;
}
};中序+后序:
递归法:
后序遍历的数组最后一个元素代表的即为根节点。知道这个性质后,我们可以利用已知的根节点信息在中序遍历的数组中找到根节点所在的下标,然后根据其将中序遍历的数组分成左右两部分,左边部分即左子树,右边部分为右子树,针对每个部分可以用同样的方法继续递归下去构造。
class Solution {
public:
TreeNode*build(vector<int>& in, vector<int>& pos,int il,int ir,int pl,int pr)
{
if(pl>pr)
return nullptr;
TreeNode*root=new TreeNode(pos[pr]);//后序遍历的最后一个节点一定是根节点
int idx=0,len=0;
for(int i=il;i<=ir;i++)
{
if(pos[pr]==in[i])
{
idx=i;
len=i-il;
break;
}
}
root->left=build(in,pos,il,idx-1,pl,pl+len-1);
root->right=build(in,pos,idx+1,ir,pl+len,pr-1);
return root;
}
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
return build(inorder,postorder,0,inorder.size()-1,0,postorder.size()-1);
}
};迭代法:
此处和前中序创建的方法大同小异,我们只需要注意前序和后序的区别即可,因为后序遍历中,和根节点挨在一块的是右子树,所以,我们转变一下思路,可以通过构建右子树的过程中插入左节点来实现,其余的原理均和前中序的原理类似。
class Solution {
public:
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
if(!postorder.size())
return nullptr;
stack<TreeNode*>st;
TreeNode* root=new TreeNode(postorder[postorder.size()-1]);
st.push(root);
int idx=postorder.size()-1;
for(int i=postorder.size() - 2;i>=0;i--)
{
TreeNode* node=st.top();
if(node->val!=inorder[idx])//这次是县创建右子树
{
node->right=new TreeNode(postorder[i]);
st.push(node->right);
}
else//找到了第一个左孩子节点
{
TreeNode* parent=nullptr;
while(!st.empty()&&st.top()->val==inorder[idx])
{
parent=st.top();
st.pop();
--idx;
}
parent->left=new TreeNode(postorder[i]);
st.push(parent->left);
}
}
return root;
}
};5.二叉树的三种迭代法遍历
题目链接:二叉树的前序遍历、二叉树的中序遍历、二叉树的后序遍历
思路分析:
前序遍历:
对于前序遍历,根左右的形式,根节点一定是最先输出的,难点在于如何转换方向,也就是当遍历到左子树最后一个节点时,如何将其转换为右子树再进行输出,此时,我们可以设置一个指针cur,初始时,cur一直向着左子树走,当左子树遍历到最左节点时,我们可以将当前的cur更新其父节点的右孩子节点,然后cur再次往左走,走到叶节点再次转向右子树,重复递归这个过程即可。
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
vector<int> ans;
stack<TreeNode*> st;
TreeNode*cur=root;
while(cur || !st.empty())
{
while(cur)
{
ans.push_back(cur->val);//将每棵子树的根节点直接加入
st.push(cur);
cur=cur->left;//接着寻找最左节点
}
//此时节点已经找到了最左节点
cur=st.top()->right;//转而进入最左节点的右子树
st.pop();//删除最左节点
}
return ans;
}
};中序遍历:
和前序遍历的大同小异,此时我们的输出模式变成了左根右,那么此时我们循环找到最左节点的时候,就需要先输出最左节点,在回溯找到根节点输出,然后再递归到右子树进行输出即可。
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
vector<int> ans;
stack<TreeNode*> st;
if(!root)
return ans;
TreeNode* cur=root;
while(cur||!st.empty())
{
while(cur)
{
st.push(cur);//将左子树根节点入栈
cur=cur->left;//向左查找最左节点
}
//此时cur已经是该子树上的最左节点
TreeNode* p=st.top();
st.pop();
ans.push_back(p->val);
cur=p->right; //无论最左节点是否有右子树,我们转换为右子树的子问题,此时cur如果为空,可直接回溯到最左节点的父节点进行操作
}
return ans;
}
};后序遍历:
后序遍历与上面的两种方式有着些许不同,其中,后序遍历的难点是如何判断当前的节点能否作为根输出,也就相当于,如果左节点存在右子树且还没有输出,那么我们就需要先考虑右子树的输出而不能先输出左节点,反之,如果其没有右子树或者右子树已经输出完了,那么就可以直接输出,所以,每个左节点都需要进行特殊分析,由于我们知道后序遍历的形式是左右根,那么每个子树输出的最后个一定是其根节点,而如果一个左节点有右子树,那么此时其后序遍历的输出,在左节点之前的节点一定是其右孩子节点,我们可以以这个条件作为其右子树是否输出完毕的条件,设置一个指针pre指向上一个被访问的节点,此时就有两种情况:
1.当前节点的右子树为空或者当前节点的右子树是上一个被访问的节点,此时说明该节点作为根节点,其右子树的输出已经完毕,可以输出根节点了;(注意此时要更新pre指针)
2.如果右树存在且没有被访问,那么就需要转到右树上去继续输出,此时根节点不能删除。
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
vector<int> ans;
stack<TreeNode*> st;
TreeNode* cur=root;
TreeNode* pre=nullptr;
while(cur || !st.empty())
{
while(cur)
{
st.push(cur);
cur=cur->left;
}
//此时已经到达了最左节点
TreeNode* top=st.top();
if(top->right==nullptr || top->right==pre) //如果此时最左节点的右子树为空或者右子树已经被访问直接输出该左节点即可
{
st.pop();
ans.push_back(top->val);
pre=top;//更新上次访问的节点
}
else
{
cur=top->right;//先访问其右子树,再输出根
}
}
return ans;
}
};后面有好的题目会继续补充,敬请期待......