当数据特征存在多重共线性,特征矩阵不满秩,或者用普通线性回归过拟合的状况时,我们需要用lasso回归或岭回归来构建模型。
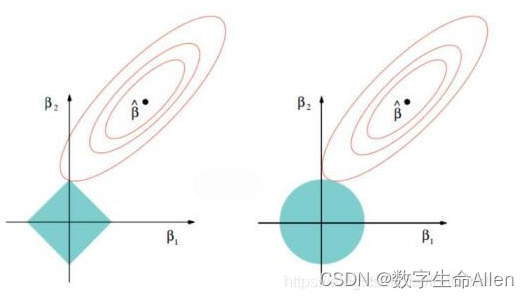
左边是lasso回归,右边是岭回归。
Lasso使用的是系数 的L1范式(L1范式则是系数 的绝对值)乘以正则化系数
岭回归使用的是系数 的L2范式(L2范式则是系数 的平方)乘以正则化系数
Lasso无法解决特征之间”精确相关“的问题。岭回归可以解决特征间的精确相关关系导致的最小二乘法无法使用的问题,而Lasso不行。Lasso不是从根本上解决多重共线性问题,而是限制多重共线性带来的影响。lasso回归会将参数降为0,会产生稀疏矩阵,但岭回归不会。
如果一个数据集在岭回归中使 用各种正则化参数取值下模型表现没有明显上升(比如出现持平或者下降),则说明数据没有多重共线性,顶多是特 征之间有一些相关性。反之,如果一个数据集在岭回归的各种正则化参数取值下表现出明显的上升趋势,则说明数据存在多重共线性。
在lasso和岭回归中,找到最优的正则化系数是最重要的,现在我们就来实战如何找到最优的正则化系数。我们以波士顿房价为例:
一.岭回归
boston = pd.read_csv(r"E:\AI课程笔记\机器学习_1\HousingData.csv") boston = boston.dropna()
print(boston.info())
# 将缺失值填充为对应列的平均值
boston = boston.fillna(mean_values) X = boston.drop(['MEDV'], axis=1) # 取出除了MEDV以外的所有特征值
y = boston['MEDV'] # 标签-房价x_train, x_test, y_train, y_test = train_test_split(X, y, random_state=22, test_size=0.2)from sklearn.linear_model import Ridge
alpharange = np.arange(75,150,10)
ridge, lr = [], []
for alpha in alpharange:
reg = Ridge(alpha=alpha)
#linear = LinearRegression()
regs = cross_val_score(reg,X,y,cv=5,scoring = "r2").mean()
#linears = cross_val_score(linear,X,y,cv=5,scoring = "r2").mean()
ridge.append(regs)
plt.plot(alpharange,ridge,color="red",label="Ridge")
#plt.plot(alpharange,lr,color="orange",label="LR")
plt.title("Mean")
plt.legend()
plt.show()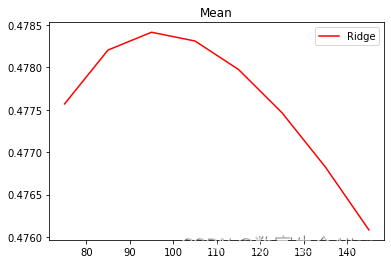
可以看到当α的值是98时,r2最大,即模型效果最好。
一.lasso回归
使用lassoCV自带的正则化路径长度和路径中的alpha个数来自动建立alpha选择的范围:
from sklearn.linear_model import LassoCV#使用lassoCV自带的正则化路径长度和路径中的alpha个数来自动建立alpha选择的范围
ls_ = LassoCV(eps=0.00001 # 正则化路径长度
,n_alphas=300 #正则化路径中俺儿α的个数
,cv=5
).fit(Xtrain, Ytrain)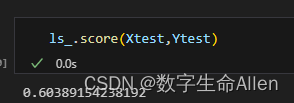
当eps为0.00001时,r2是0.603891,我们来调整eps的值去获得更好的r2.
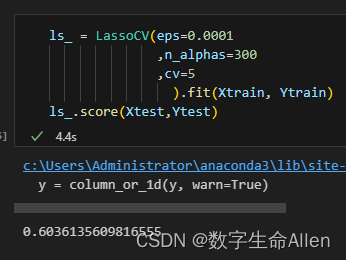
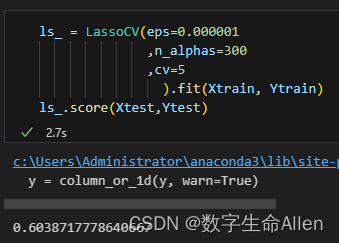
可以看出,eps为0.00001时模型效果最好。